1. На очередную неделю барон Мюнхгаузен планирует выполнить 13 разных дел (одно из которых Подвиг). Сколько различных расписаний возможно запланировать на Понедельник, если в этот день надо сделать ровно 3-и каких-нибудь дела и Подвиг среди них обязателен. При этом порядок дел следует считать существенным, важным из-за обычно разных при разных порядках дел результатах.
2. Вычислить: а) 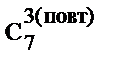 ; б)
; б) 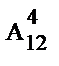 ; в)
; в) 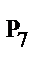 ; г)
; г) 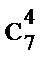 .
.
3. Сколько у студента имеется вариантов сдачи сессии с 3-мя предметами (и возможными оценками по ним: “НеУд”, “Уд”, “Хор”, “Отл”), если хотя бы один из них (какой-нибудь) он наверняка сдаст на “Отл”? (Подсказка: задачу можно решать разными способами, но легче – через поиск количества вариантов, противоположного искомому)
4. Для написания картины решено использовать какую-то одну технику – либо “карандашную” либо “фломастерную”. Сколько для этого имеется способов выбрать 3 однотипных объекта из 7 разных Карандашей и 5 разных Фломастеров?
5. Сколько есть способов одеть 7 девушек, если в универмаг завезли 3 фасона платьев – от Кардена, от Валентино, от Зайцева?
6. Из урны, содержащей красные, черные и белые шары, выбирается один шар. Пусть событие А = {выбран красный шар}, В = {выбран черный шар}, С = {выбран белый шар}. Что означают события: 1) 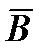 ; 2) АС+В; 3)
; 2) АС+В; 3) 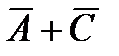 .
.
7. В магазине продаются пирожные четырех сортов; эклеры, слоеные, песочные и бисквитные. Сколькими различными способами можно купить набор из 5 пирожных?
8. В классе 30 учеников. Из них 17 посещают факультатив по английскому языку. 12 учеников посещают факультатив по математике. Всего учеников, посещающих хотя бы один факультатив, 21. Сколько только один?
9. На заседании Думы 9 депутатов записались на выступления. Какова вероятность, что двое депутатов окажутся записанными под определенными номерами?
10. Пятеро студентов сдали экзамен и получили положительные отметки. Какова вероятность, что трое получили одинаковые отметки, а двое различные? Считать, что отметки 3, 4, 5 равновозможны для каждого.
11. Среди кандидатов в студенческий совет факультета 3 первокурсника, 5 второкурсников и 7 третьекурсников. Из этого состава наудачу выбирают пять человек на предстоящую конференцию. Найти вероятность того, что будет выбран следующий состав: 1 первокурсник, 2 второкурсника, 2 третьекурсника.
Типовой вариант к модульной контрольной работе №1
1. В классе 30 учеников. Из них 15 посещают факультатив по английскому языку. 10 учеников посещают факультатив по математике. Всего учеников, посещающих хотя бы один факультатив, 20. Сколько учеников посещают оба факультатива? Сколько только один?
2. Сколькими способами можно расставить на книжной полке десятитомник М. Булгакова, располагая их так, чтобы I, V и IX тома стояли рядом (в любом порядке)?
3. Из элементов (цифр) 2, 4, 5 составить все размещения и сочетания с повторениями и без повторений по два элемента.
4. В магазине имеется 7 видов тортов. Сколькими способами можно составить набор, содержащий 3 торта? А если имеются 3 вида тортов, а нужен набор из 7 тортов?
5. Пять человек вошли в лифт на 1-м этаже девятиэтажного дома. Сколькими способами пассажиры могут выйти из лифта на нужных этажах?
6. Каждый из двух стрелков производит по одному выстрелу в мишень. Пусть событие А={первый стрелок попал в цель}, событие В={второй стрелок попал в цель}. Что означают события: а) А+В; б) 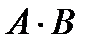 ; в)
; в) 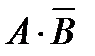 ?
?
7. В урне 12 пронумерованных шаров. Опыт состоит в извлечении одного шара из урны. Требуется: 1) указать, какие из пар событий А, В, С, D совместны, а какие нет и почему; 2) указать какие из этих пар образуют полную группу, а какие нет и почему; 3) привести примеры невозможного и достоверного событий.
8. Вычислить: 1) 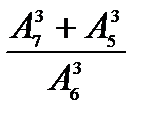 ; 2)
; 2) 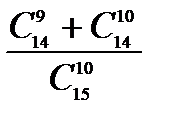 .
.
9. На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность P(A) того, что взятый наудачу подшипник окажется стандартным.
10. В урне 10 шаров: 3 белых и 7 черных. Из урны вынимают сразу два шара. Какова вероятность того, что оба шара окажутся белыми?
11. В книжном магазине на полке 10 различных книг, причем 5 книг стоят по 4 рубля каждая; 3 книги – по одному рублю и две книги – по 3 рубля. Найти вероятность того, что взятые наугад две книги стоят 5 рублей.
Контрольная работа оценивается в 30 баллов.
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Баллы | 4 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 2 | 3 | 3 |
Дата: 2018-11-18, просмотров: 1385.