2.1. В урне 3 белых, 5 синих, 12 черных шаров. Вынули один шар. Определить вероятность того, 1) что он синий, 2) что он не белый.
2.2. Бросают две игральные кости. Какова вероятность того, что наибольшее количество очков из двух костей равно 4?
2.3. Из цифр 1, 5, 9 случайным образом составляют трехзначное число без повторяющихся цифр. Какова вероятность того, что получится число: а) большее 500; б) квадратный корень из которого не больше 24; в) кратное трем; г) кратное девяти?
2.4. Какова вероятность того, что случайным образом выбранное двузначное число будет делиться на 13?
2.5. Монету подбрасывают три раза. Какова вероятность того, что: а) все три раза выпадет «решка»; б) «решка» выпадет в два раза чаще, чем «орел»; в) «орел» выпадет в три раза чаще, чем «решка»; г) при первом и третьем подбрасывании результаты будут различны?
2.6. Бросают две игральные кости. Какова вероятность того, что количества очков на двух костях равны?
2.7. 17 точек из 50 покрашены в синий цвет, а 13 точек из оставшихся покрашены в оранжевый цвет. Какова вероятность того, что случайным образом выбранная точка окажется: а) синей; б) не оранжевой; в) окрашенной; г) не окрашенной?
2.8. Бумагу со словом «ротор» разрезали на пять частей так, что на каждом кусочке оказалась одна буква. Затем последовательно наугад достают три буквы. Какова вероятность того, что получилось слово «рот»?
2.9. На заводе произвели 1000 деталей. Известно, что 100 из них бракованных. Найти вероятность того, что из 10 наугад взятых деталей ровно 1 – бракованная.
2.10. В плитке шоколада размером 3x6 случайно выбрали дольку 1x1. Какова вероятность того, что выбрали крайнюю, но не угловую дольку?
2.11. Бросают две игральные кости. Какова вероятность того, что сумма очков на двух костях равна 7?
2.12. Бросают две игральные кости. Что вероятнее, что сумма очков на двух костях равна 6 или она равна 9?
2.13. Бросают две игральные кости. Какова вероятность того, что произведение очков на двух костях равно 12?
2.14. Бросают две игральные кости. Какова вероятность того, что число очков на каждой из костей не больше 4?
2.15. В мешке лежат 33 жетона, помеченные буквами русского алфавита. Из него извлекают жетоны и записывают соответствующие буквы, причем вынутые жетоны обратно не возвращают. Какова вероятность того, что при этом получится слово «осел», «окно»? слово «аршин»?
2.16. Из цифр 4, 6, 7 случайным образом составляют трехзначное число без повторяющихся цифр. Какова вероятность того, что получится: а) наибольшее из всех таких чисел; б) число, у которого вторая цифра 7; в) число, заканчивающееся на 6; г) число, кратное 5?
2.17. Монету подбрасывают три раза. Какова вероятность того, что: а) в последний раз выпадет «решка»; б) ни разу не выпадет «орел»; в) число выпадений «орла» в два раза больше числа выпадений «решки»; г) при первых двух подбрасываниях результаты будут одинаковы?
2.18. В колоде 54 карты (две из них джокеры). Вытаскивается одна карта. Какова вероятность того, что она картинка (валет, дама, король)?
2.19. Случайным образом выбрали двузначное число. Найдите вероятность того, что оно: а) оканчивается нулем; б) состоит из одинаковых цифр; в) больше 27 и меньше 46; г) не является кубом другого целого числа.
2.20. В ящике лежат 20 одинаковых на ощупь шаров: 12 белых и 8 черных. Из ящика вынули наудачу восемь шаров. Чему равна вероятность того, что: 1) ровно три из них черных; 2) черных шаров вынули не более трех?
2.21. В ящике лежат 13 зеленых, 10 красных и 7 синих одинаковых на ощупь шаров. Наудачу вынимают 8 шаров. Чему равна вероятность того, что вынули: 1) 3 зеленых, 2 красных и 3 синих шара; 2) 1 зеленый, 5 красных и 2 синих шара?
2.22. На карточках выписаны цифры 1, 2, 3, 4, 5, 6, 7, 8 и 9. Наугад берут четыре карточки и выкладывают их в ряд. Какова вероятность того, что: 1) получится четное число;2) получится число 1234?
2.23. Из семи лотерейных билетов два выигрышных. Семь человек по очереди берут по билету (не возвращая его обратно). Чему равна вероятность выигрыша и зависит ли она от места в очереди?
2.24. В ящике лежит 31 деталь первого сорта и 6 деталей второго сорта. Наудачу вынимают три детали. Чему равна вероятность того, что: 1) все три детали первого сорта; 2) хотя бы одна из трех вынутых деталей первого сорта; 3) хотя бы одна из трех вынутых деталей второго сорта?
2.25. В коробке находятся 3 черных, 4 красных и 5 синих карандашей. Наугад вынимается один карандаш. Найти вероятность того, что вынутый карандаш: 1) черный; 2) красный; 3) синий; 4) не черный; 5) не красный; 6) не синий; 7) зеленый; 8) или черный, или красный, или синий.
2.26. В книжном магазине на полке 10 различных книг, причем 5 книг стоят по 4 рубля каждая, 3 книги – по одному рублю и две книги – по 3 рубля. Найти вероятность того, что взятые наугад две книги стоят 5 рублей. Найти вероятность того, что взятые наугад три книги будут стоить 5 рублей.
Геометрическая вероятность
3.1. В прямоугольнике АВС D отметили середины K и L сторон CD и AD соответственно, а также M и N на сторонах AB и BC так, что AM : MB=1:3 и BN : NC=1:2. В прямоугольнике случайно отметили точку. Какова вероятность того, что эта точка окажется: а) в треугольнике KCN; б) в треугольнике MBN; в) вне треугольника AMC; г) в четырехугольнике MNKL?
3.2. Случайным образом выбирают одно из решений неравенства 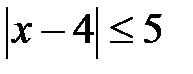 . Какова вероятность того, что оно окажется и решением неравенства: а)
. Какова вероятность того, что оно окажется и решением неравенства: а) 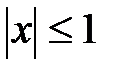 ; б)
; б) 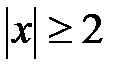 ; в)
; в) 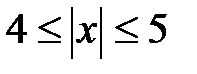 ; г)
; г) 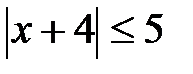 ?
?
3.3. Сектор А занимает половину рулетки, а ее вторая половина разделена на два одинаковых сектора Б и В. Какова вероятность того, что после раскручивания стрелка рулетки остановится: 1) на секторе А; 2) на секторе В?
3.4. На отрезке АВ=15 см произвольным образом выделен отрезок MN=3 см. На отрезке АВ случайным образом отмечается точка Х. Какова вероятность того, что эта точка попадет на отрезок MN?
3.5. Дано: АВ=12 см, АМ=2 см, М N=4 см. На отрезке АВ случайным образом отмечается точка Х. Какова вероятность того, что точка Х попадет на отрезок: 1) АМ; 2) А N; 3) MN; 4) МВ; 5) АВ.
3.6. Внутри квадрата со стороной 10см выделен круг радиусом 2см. Случайным образом внутри квадрата отмечается точка. Какова вероятность того, что она попадет в выделенный круг?
3.7. На отрезок длины 1 бросают наудачу две точки. Они разбивают отрезок на три отрезка. Какова вероятность, что из полученных трех отрезков можно сложить треугольник? Найти вероятность того, что из трех наудачу взятых отрезков, длина каждого из которых не превосходит а, можно составить треугольник.
3.8. Какой толщины должна быть монета, чтобы вероятность падения на ребро равнялась 1/3?
3.9. Наудачу выбирают два числа из промежутка [0, 1]. Какова вероятность того, что их сумма заключена между 1/4 и 1?
3.10. Какова вероятность того, что произведение двух наудачу взятых правильных положительных дробей будет не больше 1/4?
3.11. На отрезок АВ длины а наудачу нанесена точка С. Найти вероятность того, что меньший из отрезков АС и ВС имеет длину, большую, чем 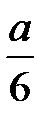 .
.
3.12. На площадку, покрытую кафельной плиткой со стороной а=6 см, случайно падает монета радиуса r=2 см. Найти вероятность того, что монета целиком окажется внутри квадрата.
Дата: 2018-11-18, просмотров: 590.