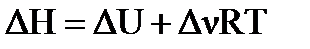Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

                                          ,                                     (23)

где: - изменение числа молей газообразных веществ в системе в результате процесса, т.е. разность сумм стехиометрических коэффициентов перед газообразными веществами в конце и начале процесса: .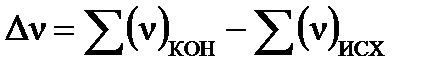

 Термохимические законы.

 Первый из них, закон Ломоносова - Лавуазье–Лапласа, формулируется следующим образом:

 Тепловой эффект прямой реакции всегда равен по абсолютной величине тепловому эффекту обратной реакции, но противоположен по знаку.

                            │ │=│- │                                                      (24)

Это означает, что при образовании любого соединения выделяется (поглощается) столько же энергии, сколько поглощается (выделяется) при его распаде на исходные вещества. Например:

2H₂(г) + O₂(г) = 2H₂О(ж) + 572 кДж (горение водорода в кислороде)

2H₂О(ж) + 572 кДж = 2H₂(г) + O₂(г) (разложение воды электрическим током)

Закон Ломоносова - Лавуазье–Лапласа является следствием закона сохранения энергии.

Второй закон термохимии был сформулирован в 1840 г российским химиком, академиком Г. И. Гессом:

 Тепловой эффект реакции зависит только от природы веществ и их агрегатного состояния в начале процесса и в его конце и не зависит от промежуточных стадий процесса.

    В термохимических расчетах используются следствия закона Гесса:

I следствие

Первое следствие из закона Гесса описывается уравнением:

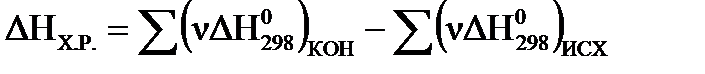               ,                                            (25)

где ν – количество молей вещества (стехиометрический коэффициент в уравнении процесса перед данным веществом); – суммы стандартных тепловых эффектов образования конечных и исходных веществ реакции. Теплота образования вещества (ΔН⁰₂₉₈, кДж/моль) – тепловой эффект реакции образования 1 моля сложного вещества из простых веществ (см. в таблице термодинамических потенциалов). Теплоты образования простых веществ принимаются равными нулю. За стандартные условия принято: давление 101,32 кПа, температура 298 К.

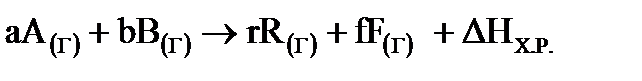
ΔН_Х.Р.= fΔН⁰₂₉₈(F) + rΔН⁰₂₉₈(R) –a ΔН⁰₂₉₈(A) –b ΔН⁰₂₉₈(B)

II следствие

Второе следствие из закона Гесса описывается уравнением:

             ,                                             (26)

ΔН_X.P.= a ΔН^сг₂₉₈(A) +b ΔН^сг₂₉₈(B) –r ΔН^сг₂₉₈(R) –f ΔН^сг₂₉₈(F),

где ΔН^сг₂₉₈ – стандартный тепловой эффект сгорания соответствующего вещества (стандартная энтальпия сгорания). Теплота сгорания вещества (ΔН^сг₂₉₈, кДж/моль) – тепловой эффект реакции окисления 1 моля вещества в избытке кислорода до высших устойчивых оксидов.

 Второй закон термодинамики – закон, определяющий возможность самопроизвольного протекания процесса и его пределов. Этот закон имеет вероятностный и статистический характер и вполне справедлив только для макросистем с очень большим количеством (N) структурных единиц  или микросостояний. Микросостояние – состояние каждой структурной единицы вещества, которое характеризуется определенными координатами и энергетическим импульсом. Направление самопроизвольного процесса определяется вторым законом термодинамики как переход системы от менее вероятного к более вероятному состоянию. А отклонения поведения системы от второго закона термодинамики тем более возможны, чем меньше частиц содержится в данной системе. Вероятность каждого макросостояния пропорциональна числу микросостояний, через совокупность которых оно осуществляется. Это число называется термодинамической вероятностью W.

 В качестве меры термодинамической вероятности (W) состояния системы во втором законе термодинамики используется термодинамический потенциал - энтропия S, Дж/моль∙К (мера хаоса в системе). В соответствии с уравнением Л.Больцмана, величина энтропии связана с термодинамической вероятностью состояния системы (W):

                                      S= k ln W ,                                                     (27)

 где k = R/N_а = 1,38×10^-23 Дж/ град - постоянная Больцмана. В процессах передачи тепловой энергии существует фактор интенсивности (это градиент температуры) и фактор емкости - энтропия.{\displaystyle dS=\delta Q/T} Термодинамическая вероятность (W) любой системы может быть рассчитана с использованием методов статистической физики. Величина энтропии в системе является функцией количества структурных единиц (N) и температуры (T):        S = f(N, T). Значение энтропии в любой системе, находящейся не при абсолютном нуле только положительно, а изменение энтропии в том или ином процессе может быть и положительно и отрицательно: S⁰₂₉₈>0, ΔS>0 и ΔS<0, S⁰₂₉₈, Дж/моль∙град.

    Известны различные формулировки второго закона термодинамики.  1) Невозможность самопроизвольного перехода тепла от менее нагретого тела к более нагретому.

 2) Невозможность создания вечного двигателя второго рода , т. е. машины, которая периодически при постоянной температуре превращает тепло среды в работу. 

Расчет изменения энтропии при протекании химического процесса.

 

Изменение энтропии химического процесса равно алгебраической сумме стандартных энтропий участников реакций с учетом их стехиометрических коэффициентов, причем энтропия продуктов реакции берутся со знаком плюс, а энтропия исходных веществ – со знаком минус.

Для реакции, протекающей по следующему уравнению:

ΔS_Х.Р. = rS⁰₂₉₈ (R) + fS^o₂₉₈(F) – aS^o₂₉₈(A) – bS^o₂₉₈(B)

 

В общем виде:

                                                                (28)

В закрытых и изолированных системах самопроизвольное протекание процесса всегда идет с увеличением энтропии (ΔS>0 ) и пределом протекания процесса является: S → S_max.

В открытых системах весь энергетический запас системы (Н= L+ G) можно разделить на две составляющие: а) связанная энергия (L=T∙S), которая обусловливает жесткие связи в самой системе и которая не может быть переведена в работу (А); б) свободная энергия (G)_Р,Т, за счет которой система совершает работу при самопроизвольном протекании процесса. Т.е. ΔG = ─ А, а т.к. А>0, то ΔG<0. Это основное условие самопроизвольного протекания процесса. (ΔG)_Р,Т (кДж/моль) является важнейшей характеристической функцией любого процесса в открытой системе и называется изобарно-изотермическим потенциалом или энергией Гиббса. В открытой системе при протекании изобарно-изотермического процесса изменения термодинамических потенциалов системы связаны в уравнение:

                                   ΔG_Х.Р. = ΔН _Х.Р. – Т∙ ΔS _Х.Р.,                                            (29)

 которое является уравнением энергетического баланса системы. Рассчитать  ΔН _Х.Р. и ΔS _Х.Р. для стандартных условий можно по I следствию из закона Гесса. Энергия Гиббса является критерием направленности самопроизвольного химического процесса и предела его протекания. Пределом протекания процесса является стремление системы к состоянию равновесия при ΔG = 0. Состояние системы называют равновесным, если все параметры остаются постоянными во времени и в системе отсутствуют потоки вещества и энергии. В состоянии равновесия энтальпийный фактор (ΔН _Х.Р.) и энтропийный (Т∙ ΔS_Х.Р.) равны по значению: ΔН _Х.Р.= Т_равн.∙ ΔS_Х.Р.. Можно рассчитать температуру равновесного состояния, приняв, что ΔН _Х.Р. и ΔS_Х.Р. не зависят от температуры:

                                     Т_равн.= ΔН _Х.Р./ ΔS_Х.Р..                                                      (30)

 

Примеры решения типовых задач

Пример 1.

 Рассчитайте тепловой эффект реакции окисления одного моля нафталина ( ) в открытой калориметрической бомбе (Р=const) при 298 К с образованием воды и оксида углерода (IV). На какую величину будет отличаться тепловой эффект этого процесса, если его проводить в закрытом сосуде (V=const) и водяной пар не конденсируется?

 

Дано: ν(С10Н8) =1моль ΔНо298(С10Н8) = 78,1 кДж/моль ΔНо298(СО2) = –393,5 кДж/моль ΔНо298(Н2О(Г)) =      –241,8 кДж/моль Тепловые эффекты образования (ΔНо298) исходных и конечных веществ в стандартном состоянии при 298 К находим в справочнике. Учесть, что теплота образования простого вещества (ΔНо298ПР.В.) равна нулю.	Решение Уравнение процесса окисления: С10Н8(К)+12О2(Г)=10СО2(Г)+4Н2О(Г). а) Определим , используя первое следствие из закона Гесса: ΔНХ.Р.=10 ΔНо298(СО2)+4 ΔНо298(Н2О(Г)) –ΔНо298(С10Н8) (кДж/моль). Процесс протекающий в открытом сосуде, является изобарным (Р=const), следовательно, ΔНХ.Р. является тепловым эффектом изобарного процесса. б) Для определения теплового эффекта (ΔUХ.Р.) изохорного процесса (V=const) (т.е. в закрытом сосуде) воспользуемся формулой пересчета: . Изменение числа молей ( ) газообразных веществ в системе равно: =4+10-12=2. (кДж/моль).
Найти: а) ΔНХ.Р.}?  б) ΔUХ.Р.}?	Ответ: Тепловой эффект процесса в изохорных условиях будет больше на 4,9 кДж.

Пример 2.

Будет ли возрастать беспорядок в системе, если в ней из газообразных хлористого водорода и аммиака образуется кристаллический хлористый аммоний? Каков знак изменения энтропии? Чему равно изменение энтропии этой системы, если образуется 5,35 граммов хлорида аммония в стандартных условиях?

Дано: m(NH4Cl(К)) = 5,35 г М(NH4Cl)= 53,5 г/моль So298(NH4Cl(К)) = 95,9 Дж/моль∙К So298(NH3(Г)) =192,6 Дж/моль∙К So298(HCl(Г))=186,8 Дж/моль∙К Значения абсолютных энтропий веществ взяты из справочника.			Решение Записываем уравнение процесса: NH3(Г)+HCl(Г)=NH4Cl(К). Из уравнения следует, что процесс идет с уменьшением числа молей (ν) вещества (Σνисх.=2, Σνкон.=1), кроме того, исходные вещества газообразные, а продукт - кристаллическое вещество. Следовательно, беспорядок в системе должен уменьшаться, уменьшается и энтропия системы, как мера беспорядка ( ). Для химической реакции изменение энтропии (ΔSХ.Р.) рассчи­таем, используя значения абсолютных энтропий веществ, по уравнению: ΔSХ.Р.= So298(NH4Cl(К))– So298(NH3(Г)) – So298(HCl(Г)), ΔSХ.Р.=95,9 –192,6 –186,8 = –283,5 (Дж/моль∙К). Данный расчет проведен с учетом образования 1 моля хлористого аммония. Для ответа на поставленный вопрос необходимо найденную величину умножить на количество молей образующегося хлористого аммония: ΔS = ΔSХ.Р.∙ ν(NH4Cl), ΔS = –283,5∙(5,35/53,5) = –28,3 (Дж/К).
Найти:ΔSХ.Р.>0? ΔSХ.Р.<0? ΔS?			Ответ: ΔSХ.Р.<0, ΔS = –28,3 Дж/К.

Пример 3.

Определите возможность процесса восстановления оксида железа (III) до свободного металла в атмосфере оксида углерода (II) в стандартных условиях.

Дано: Т=298 К Тепловые эффекты образования (ΔНо298) и значения абсолютных энтропий (So298) исходных и конечных веществ в стандартном состоянии находим в справочнике: ΔНо298(СО2(Г))= −393,5   ΔНо298(СО(Г))= –110,5   ΔНо298(Fe2O3(К)) =  –822,7   So298(СО2(Г)) = 213,7 So298(Fe(К)) = 27,2 So298(Fe2O3(К)) = 87,5 So298(СО(Г)) =197,3		Решение. Уравнение процесса: Fe2O3(К)+3 СО(Г)=2 Fe(К)+3 СО2(Г).                              Условием самопроизвольного протекания процесса является отрицательное изменение энергии Гиббса (ΔG<0), рассчитать которое можно по уравнению:  ΔGХ.Р. = ΔН Х.Р. – Т∙ ΔS Х.Р..                                              Учитывая, что реакция протекает в стандартных условиях, рассчитаем ΔНХ.Р. и ΔSХ.Р.по первому следствию из закона Гесса при восстановлении 1 моля Fe2O3. а) ΔНХ.Р.=3∙ ΔНо298(СО2(Г))–3 ∙ΔНо298(СО(Г)) –  –ΔНо298(Fe2O3(К)),                                            ΔН Х.Р.=3∙ (–393,5) –3∙ (–110,5) – (–822,7) =  –26,3 кДж/моль;                                            б) ΔSХ.Р.=3∙ So298(СО2(Г))+2 ∙So298(Fe(К)) –      –3∙ So298(СО(Г)) – So298(Fe2O3(К)) ,                                                                                            ΔSХ.Р.=3∙213,7+2∙27,2 –3∙ 197,3 – 87,5 =16,1 Дж/моль∙К                                              ΔGХ.Р. = –26,3 –298 ∙ 16,1∙10-3 = –31,1 .
Найти: ΔGХ.Р.?		Ответ: Т.к. ΔGХ.Р.<0, следовательно, реакция восстановления в стандартных условиях возможна.

Пример 4.

 Определите изменение внутренней энергии при испарении 0,50 кг воды при 290 К, допуская, что пары воды подчиняются законам идеальных газов. Удельная теплота парообразования при данной температуре составляет 2451 Дж/г.

 

Дано: m(H2O) =0,50 кг m(H2O) =500 г Т = 290К ΔНуд исп.=2451 Дж/г ΔНуд исп.=2,451 кДж/г R =8,31∙10-3 кДж/моль∙К		Решение. Уравнение процесса: H2O(Ж)→ H2O(Г). а) Испарение это эндотермический фазовый переход, для которого изобарный тепловой эффект: ΔНисп.>0. Рассчитываем тепловой эффект испарения 0,500 кг воды: ΔНисп.= ΔНуд исп.∙ m(H2O), ΔНисп. = 2,451∙500 = 1225,50 кДж. б) Изменение внутренней энергии (ΔUисп.) определяем, используя формулу пересчета теплового эффекта с изобарных на изохорные условия: ( 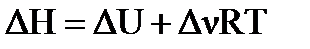) ΔUисп.= ΔНисп. – RT; - изменение числа молей газообразных веществ в системе в результате процесса будет определяться тем количеством молей воды, которые находятся в начале процесса в жидкой фазе и переходят в газ:  = m(H2O)/М(H2O),  =500/18 =27,78 моль. ΔUисп. = 1225,50 – 27,78∙8,31∙10-3∙290 = 1158,55 кДж.
Найти: ΔUисп.}?		Ответ: ΔUисп. =1158,55 кДж.

Пример 5.

    При какой температуре система, в которой протекает процесс: 2NO_2(Г) ↔ 2NO_(Г)  +O_2(Г), приходит к состоянию равновесия? В какую сторону надо сдвинуть температуру, чтобы в ней протекало преимущественно прямое направление процесса? Возможно ли прямое направление процесса в стандартных условиях? Принять, что изменения термодинамических функций процесса от температуры не зависят.

Дано: ΔНо298(NО2(Г))=33,5 кДж/моль ΔНо298(NО(Г))=90,3 кДж/моль So298(NО2(Г))=240,3 Дж/моль∙К So298(NО(Г))=210,7 Дж/моль∙К So298(О2(Г))=205,2 Дж/моль∙К		Решение. Уравнение процесса: 2NO2(Г)↔ 2NO(Г)  + O2(Г). ΔНХ.Р., ΔSХ.Р. находим по первому следствию из закона Гесса: а) ΔНХ.Р.=2 ΔНо298(NО(Г)) –2 ΔНо298(NО2(Г)), ΔНХ.Р.=2∙90,3–2∙33,5 = 113,6 кДж (т.к. ΔНХ.Р.>0, прямое направление процесса является эндотермическим); б) ΔSХ.Р.= 2 So298(NО(Г)) + So298(О2(Г)) – 2 So298(NО2(Г)), ΔSХ.Р.= 2∙210,7 + 205,2 – 2∙240,3 = 146,0 Дж/К = 0,146 кДж/К. в) Для состояния равновесия ΔGХ.Р.=0, отсюда: ΔНХ.Р.= Травн.∙ΔSХ.Р., Травн. = ΔНХ.Р./ ΔSХ.Р., Травн.= 113,6/0,146=778 К. г) ΔG298 = ΔНХ.Р. – Тст. ∙ ΔSХ.Р.,  ΔG298 = 113,6 – 298∙0,146 = 70,1 кДж.
Найти: а) ΔНХ.Р.}? б) ΔSХ.Р.}? в)Травн.}? г)ΔG298}?		Ответ: Травн.= 778 К; т.к. прямое направление процесса является эндотермическим, то для протекания прямого направления процесса температуру от равновесного значения необходимо увеличить; т.к. ΔG298>0, то в стандартных условиях прямое направление процесса невозможно.

 

          Контрольные вопросы и задания

Вариант 1.

1. Для реакции указажите условие (Р-const или V- const), при котором тепловой эффект реакции будет большим. Возможен ли этот процесс в стандартных условиях? Ответ подтвердите расчетом.

2. Определите изменение внутренней энергии при испарении 250 г воды при 290 К, допуская, что пары воды подчиняются законам идеальных газов. Удельная теплота парообразования при данной температуре составляет 2451 Дж/г.

3. Возможно ли устойчивое существование оксида меди (II) в атмосфере водорода? Ответ подтвердите термодинамическим расчетом.

4. Сколько теплоты выделится при сжигании 920 г этанола? Запишите термохимическое уравнение данной реакции.

5. С помощью термодинамических расчетов на примере реакций

SnO_{2 (к)} + Sn _(к) = 2SnO_(к)  и  PbO_2(к) + Pb_(к) = 2PbO_(к) ответьте на вопрос об устойчивых степенях окисления олова и свинца в закрытой системе при температуре 300 К.

Вариант 2.

1. Найдите тепловой эффект процесса получения 5,5 кг хлористого метила (СH₃Cl) из газообразных метана и хлора. Процесс протекает в закрытом сосуде (автоклаве) при 298 К.

2. Возможно ли устойчивое существование оксида меди (II) в атмосфере водорода? Ответ подтвердите термодинамическим расчетом.

3. Определите изменение энтропии при плавлении 82 г NaF (фтористый натрий), если энтальпия плавления равна 33,45 кДж/моль, а температура плавления 996 ⁰С.

4. Найдите массу метана, при полном сгорании которой ( с образованием жидкой воды)выделяется теплота , достаточная для нагревания 100 г воды от 20^оС до 30^оС. Мольную теплоемкость воды принять равной 75,3 Дж/моль∙К.

5. При взаимодействии метана и сероводорода образуются газообразный водород и жидкий сероуглерод (CS₂). Вычислите изменение энтальпии и энтропии процесса в стандартных условиях. Определите температуру начала прямой реакции.

Вариант 3.

1. Водяной газ представляет собой смесь равных объемов водорода и оксида углерода (II). Найдите количество теплоты, выделяющейся при сжигании 112 л водяного газа, взятого при нормальных условиях.

2. Вычислите изменение внутренней энергии при испарении 32 г метанола при температуре кипения 65,7 ⁰С, если удельная теплота испарения составляет 1,104 кДж/г.

3. Нитрат аммония может разлагаться по двум направлениям:

                а) NH₄NO_3(K) → N₂O_(Г) + 2H₂O_(Г); 

             б) NH₄NO_3(K) → N₂₍₎ + 0,5O_2(Г) + 2H₂O_(Г).

Термодинамическим расчетом подтвердите, какая из приведенных реакций наиболее вероятна в стандартных условиях.

4. Возможно ли восстановление в стандартных условиях оксида алюминия водородом? При какой температуре эта реакция теоретически становится возможной?

5. Найдите изменение энтропии открытой системы, если в ней протекает процесс разложения фосгена про уравнению: COCl_2(Г) → CO_(Г) + Cl_2(Г) и разлагается только 50 % содержащегося фосгена.

Вариант 4.

1. Найдите количество теплоты, выделяющейся при взрыве 8,4 л гремучего газа, взятого при нормальных условиях.

2. Рассчитайте изменение энтропии для реакции полного окисления 32-х г сернистого газа кислородом в стандартных условиях в открытой системе.

3. Термодинамическим расчетом докажите, протекает ли прямой процесс в системе:  SO_2(Г) + 0,5O_2(Г) ↔ SO_3(Г) в стандартных условиях. При какой температуре он становится возможным?

4. Возможно ли существование в природных условиях Земли свободного металлического натрия? Ответ подтвердите термодинамическим расчетом.

5. Рассчитайте изменение внутренней энергии при испарении 1 кг воды при 423 К, если теплота испарения при этой температуре равна 2110 кДж/кг. Считать пар идеальным газом.

Вариант 5.

1. Какое количество тепла поглощается или выделяется в час на обогатительной фабрике при обжиге сульфидной руды цинка (ZnS) до получения оксида цинка, если производительность фабрики составляет 100 кг руды в час?

2. Будет ли возрастать беспорядок в системе, если в ней из газообразных хлористого водорода и аммиака образуется кристаллический хлористый аммоний? Каков знак изменения энтропии при этом? Чему равно изменение энтропии этой системы, если образуется 5,35 г хлористого аммония в стандартных условиях?

3. Определите тепловой эффект, изменение энтропии и изменение внутренней энергии системы, в которой происходит испарение 3,1 кг жидкого метиламина (CH₅N) при 298 К, если мольное изменение энтальпии в данном фазовом переходе составляет 24,28 кДж/моль.

4. Какая степень окисления для свинца наиболее устойчивая при стандартных условиях в системе: PbO_(K) + 0,5O_2(Г) = PbO_2(K)?. Докажите термодинамическим расчетом.

5. При какой температуре начинается процесс разложения карбоната кальция на оксид кальция и углекислый газ? В сторону увеличения или уменьшения надо сдвинуть температуру от равновесного значения, чтобы процесс пошел только в прямом направлении? Возможен ли этот процесс при стандартной температуре?     

Вариант 6.

1.  Сколько теплоты выделится при сжигании 580 г жидкого ацетона (С₃Н₆О)? Запишите термохимическое уравнение данной реакции.

2. Определите возможность процесса восстановления оксида железа (III) до свободного металла в атмосфере оксида углерода (II) в стандартных условиях.

3. Рассчитайте тепловой эффект реакции окисления одного моля нафталина         ( ) в открытой калориметрической бомбе при 298 К с образованием газообразной воды и диоксида углерода. На какую величину будет отличаться тепловой эффект этого процесса, если его проводить в закрытом сосуде и водяной пар не конденсируется?

4. Какие из перечисленных оксидов могут быть восстановлены алюминием до свободного металла при стандартных условиях: CaO, FeO, CuO, PbO, Fe₂O₃, Cr₂O₃? Докажите термодинамическими расчетами.

5. При  энтропия ромбической серы , а моноклинной . Энтальпии сгорания соответственно равны: . Рассчитайте, возможно ли превращение  при

 

Вариант 7.

1. Термит  используется для термической сварки стальных изделий. Какое количество теплоты выделяется, если используется термит массой 1 кг?

2. При какой температуре начинается процесс разложения карбоната бария на оксиды? В какую сторону (увеличения или уменьшения) надо сдвинуть температуру от равновесного значения, чтобы процесс протекал только в прямом направлении?

3. Возможно ли восстановление никеля из его оксида водородом до свободного металла при 298 К? При какой температуре эта реакция становиться возможной? Ответ подтвердите расчётом.

4. Определите тепловой эффект, изменение энтропии и изменение внутренней энергии системы, в которой происходит испарение 3,1 кг жидкого метиламина (CH₅N) при 298 К, если мольное изменение энтальпии в данном фазовом переходе составляет 24,28 кДж/моль.

5. Термодинамическим расчетом докажите, какая степень окисления серы наиболее устойчива при стандартных условиях в системе 2SO_3(Г) + S_(K) ↔ 3SO_2(Г).

 

Вариант 8.

1. Для реакции укажите условие (P=const или V=const), при котором тепловой эффект будет бóльшим. Возможен ли процесс в стандартных условиях?

2. Вычислить изменение внутренней энергии при испарении 119,5 г хлороформа (CHCl₃) при температуре кипения 334,3 К, если мольная  теплота испарения составляет 29,52 кДж/моль.

3. При какой температуре начинается процесс разложения карбоната магния на оксиды? В какую сторону (увеличения или уменьшения) надо сдвинуть температуру от равновесного значения, чтобы процесс протекал только в прямом направлении?

4. Возможно ли существование в природных условиях Земли свободного металлического алюминия? Ответ подтвердите термодинамическим расчетом.

5. Какие из перечисленных оксидов могут быть восстановлены алюминием до свободного металла при стандартных условиях: MgO, FeO, CuO, NiO, Fe₂O₃, ? Докажите термодинамическими расчетами.

Вариант 9.

1. Какое количество тепла поглощается или выделяется в час на обогатительной фабрике при обжиге сульфидной руды меди (CuS) до получения оксида меди (II), если производительность фабрики составляет 100 кг руды в час?

2. При  энтропия ромбической серы , а моноклинной . Энтальпии сгорания соответственно равны: . Рассчитайте, возможно ли превращение  при

3. Сколько теплоты выделится при сжигании 58,0 г жидкого ацетона (С₃Н₆О)? Запишите термохимическое уравнение данной реакции.

4. Термодинамическим расчетом докажите, какая степень окисления серы наиболее устойчива при стандартных условиях в системе 2SO_3(Г) + S_(K) ↔ 3SO_2(Г).

5. Будет ли возрастать беспорядок в системе, если в ней из газообразных хлористого водорода и аммиака образуется кристаллический хлористый аммоний? Каков знак изменения энтропии при этом? Чему равно изменение энтропии этой системы, если образуется 53,5 г хлористого аммония в стандартных условиях?

Вариант 10.

1. Рассчитайте тепловой эффект реакции окисления одного моля нафталина         ( ) в открытой калориметрической бомбе при 298 К с образованием газообразной воды и диоксида углерода. На какую величину будет отличаться тепловой эффект этого процесса, если его проводить в закрытом сосуде и водяной пар  конденсируется?

2. Определите массу серного колчедана (FeS₂), окисленного до оксидов серы (IV) и железа (III) при стандартной температуре, если количество теплоты, выделившейся при этом, составило 6884,5 кДж.

3. При какой температуре начинается процесс разложения гидроксида магния на оксид магния и воду (пар)? В какую сторону (увеличения или уменьшения) надо сдвинуть температуру от равновесного значения, чтобы процесс протекал только в прямом направлении?

4. Возможно ли восстановление никеля из его оксида водородом до свободного металла при 298 К? При какой температуре эта реакция становиться возможной? Ответ подтвердите расчётом.

5. Нитрат аммония может разлагаться по двум направлениям:

а) NH₄NO_3(K) → N₂O_(Г) + 2H₂O_(Г); б) NH₄NO_3(K) → N₂₍₎ + 0,5O_2(Г) + 2H₂O_(Г).

Термодинамическим расчетом подтвердите, какая из приведенных реакций наиболее вероятна в стандартных условиях.

Вариант 11.

1. Найдите массу метана, при полном сгорании которой ( с образованием жидкой воды)выделяется теплота , достаточная для нагревания 1000 г воды от 20^оС до 30^оС. Мольную теплоемкость воды принять равной 75,3 Дж/моль∙К.

2. Термит  используется для термической сварки стальных изделий. Какое количество теплоты выделяется, если используется термит массой 0,5 кг?

3. Найдите изменение энтропии открытой системы, если в ней протекает процесс разложения фосгена про уравнению: COCl_2(Г) → CO_(Г) + Cl_2(Г) и разлагается только 50 % содержащегося фосгена.

4. При какой температуре начинается процесс разложения карбоната бария на оксид бария и углекислый газ? В сторону увеличения или уменьшения надо сдвинуть температуру от равновесного значения, чтобы процесс пошел только в прямом направлении? Возможен ли этот процесс при стандартной температуре?

5.   Определите тепловой эффект, изменение энтропии и изменение внутренней энергии системы, в которой происходит испарение 6,2 кг жидкого метиламина (CH₅N) при 298 К, если мольное изменение энтальпии в данном фазовом переходе составляет 24,28 кДж/моль.

Вариант 12.

1. Найдите тепловой эффект процесса получения 0,55 кг хлористого метила (СH₃Cl) из газообразных метана и хлора. Процесс протекает в открытой системе (Р=101,32 кПа) при 298 К.

2. Определите тепловой эффект, изменение энтропии и изменение внутренней энергии системы, в которой происходит испарение 3,1 кг жидкого метиламина (CH₅N) при 298 К, если мольное изменение энтальпии в данном фазовом переходе составляет 24,28 кДж/моль.

3. Термодинамическим расчетом докажите, протекает ли прямой процесс в системе:  SO_2(Г) + 0,5O_2(Г) ↔ SO_3(Г) в стандартных условиях. При какой температуре он становится возможным?

4. Какие из перечисленных оксидов могут быть восстановлены алюминием до свободного металла при стандартных условиях: NiO, FeO, CuO, SnO, Fe₂O₃, Al₂O₃? Доказать термодинамическими расчетами.

5. При взаимодействии метана и сероводорода образуются газообразный водород и жидкий сероуглерод (CS₂). Вычислить изменение энтальпии и энтропии процесса в стандартных условиях. Определить температуру начала прямой реакции.

 

4.2. Кинетика химических процессов и химическое равновесие

4.2.1. Формальная кинетика

Химическая кинетика рассматривает скорости и механизмы протекания химических реакций. Основными параметрами, от которых зависит скорость реакции (υ), являются: природа реагирующих веществ, концентрация веществ в системе, температура и наличие катализатора. При кинетическом исследовании определяют изменение концентрации веществ  во времени .  Скорость химической реакции это число элементарных актов взаимодействия веществ, происходящих в единицу времени, в единице объема (для гомогенных реакций) или на единицу поверхности межфазной границы(для гетерогенных реакций). 

     Для реакций, описываемых стехиометрическим уравнением:

,

где: a,b,r,f – стехиометрические коэффициенты веществ: А, В, R, F, участвующих в процессе, соответственно, истинная скорость (υ) выражается соотношением: .                                   (31)

    Зависимость скорости реакции от природы и концентрации реагирующих веществ выражается  кинетическим уравнением процесса и является частным случаем закона действующих масс:

                           ,                                                                 (32)

где: k – константа скорости реакции, - концентрации веществ А и В.

При постоянной температуре (Т= const ) скорость элементарной химической реакции прямо пропорциональна произведению концентраций реагирующих веществ, причем концентрация каждого вещества взята в степени, равной соответствующему коэффициенту перед данным веществом в уравнении процесса.

Численное значение константы скорости реакции (k) или нулевой скорости процесса (при Т=const и = 1 моль/л) определяется только природой взаимодействующих веществ.

Сумма показателей степени молярных концентраций веществ в кинетическом уравнении называется порядком реакции (n). Это строго экспериментальная величина, показывающая характер зависимости скорости реакции от концентрации. Порядок реакции связан с механизмом и молекулярностью реакции. Молекулярность реакции определяется количеством частиц, одновременно вступающих в акт химического взаимодействия. Реакция, в результате которой молекулы исходных веществ непосредственно превращаются в молекулы продуктов реакции, называется элементарной или простой. Молекулярность таких реакций максимально может равняться трем.  Реакции, уравнения которых содержат большое число частиц, протекают по сложному механизму, т.е. являются последовательными, параллельными, последовательно-параллельными и т.д.. Сложные реакции представляют собой совокупность элементарных реакций или стадий. Общая скорость сложной реакции определяется скоростью самой медленной стадии процесса, которая называется лимитирующей.

    Для элементарных реакций молекулярность и порядок обычно совпадают, а для реакций различной молекулярности закон действующих масс будет выражаться различным образом:

а) для реакций нулевого порядка, которые протекают с постоянной скоростью в течение длительного времени, за счет большого избытка исходного вещества и, следовательно, постоянства его концентрации:  или в интегральном виде ; 

б) для реакций первого порядка:                                               (33)

 или в интегральном виде 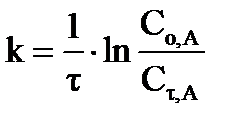, ;                             (34)

где - исходная концентрация реагента и концентрация в момент времени , соответственно, время полураспада  (время, в течение которого исходная концентрация вещества уменьшается вдвое) будет определяться: ;

в) для реакций второго порядка, если начальные концентрации исходных веществ одинаковы ( ):  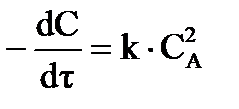                                       (35)

или в интегральном виде: , ;

г) для реакций второго порядка, если начальные концентрации исходных веществ неодинаковы :        ,                         (36)

в интегральной форме:   ;

д) для реакций третьего порядка, если начальные концентрации исходных веществ одинаковы:                                                                     (37)

или в интегральном виде: ,

 время полураспада определяется: .

4.2.2. Зависимость скорости реакции от температуры

Влияние температуры на скорость реакции приближенно выражается правилом Вант-Гоффа: скорость реакции при увеличении температуры на 10^о для большинства химических реакций увеличивается в 2 – 4 раза,

                 ,                                                                       (38)

где:  - константы скорости при температурах Т₁ и Т₂ (Т₂>Т₁); γ - температурный коэффициент скорости ( ).

Зависимость скорости реакции от температуры в широком интервале температур выражается уравнением Аррениуса, которое в интегральной форме имеет вид:

 , ,                                          (39а, 39б)    

где: Е_А - энергия активации;  - предэкспоненциальный множитель.

Для процессов, подчиняющихся правилу Вант-Гоффа, энергия активации и температурный коэффициент связаны уравнением:

                                .                                     (39в)

Любой процесс, в зависимости от природы реагирующих веществ, имеет свой энергетический порог. Только те частицы, которые имеют запас энергии, соизмеримый с энергией порога (Е_п), при столкновении вступают во взаимодействие с разрывом химических связей и образованием новых связей, т.е. образуются новые вещества. Тот избыток энергии по сравнению с энергией исходного состояния системы (Е_исх), который позволяет реагирующим частицам достичь энергетического порога, называется энергией активации (Е_А) (рис.14). В зависимости от величины энергии активации реакции протекают с различной скоростью. Если энергия активации очень низкая, реакция протекает с очень большой скоростью (реакции взрыва). Реакции с очень большой энергией активации протекают очень медленно (распад трансурановых элементов в земной коре). Понизить энергию активации системы ( ), а, следовательно, увеличить скорость реакции, можно применив положительный катализатор. Катализатор – это вещество участвующее в процессе, но на последней стадии выделяющееся в неизменном виде. В присутствии катализатора механизм реакции изменяется так, что это приводит к понижению энергии активации реакции ( ) (рис.14) и увеличению скорости реакции, иногда во много тысяч раз.

В гетерогенных системах на скорость реакции, кроме перечисленных выше факторов, влияет степень дисперсности (степень раздробленности) конденсированной (твердой) фаза и скорость переноса вещества в системе (k^′). Концентрация вещества, находящегося в твердой фазе, является величиной постоянной (const), и она входит в константу скорости (k=k^′∙ const). Для гетерогенной реакции в общем виде  aА_(К) +b В_(Г) = dD_(Г)  кинетическое уравнение можно записать

                              .

ЕП

Еисх.

Е, эВ

Ход процесса

Рис.14 Энергетическая диаграмма процесса.

Екон

                                                          (39)

 

4.2.3. Химическое равновесие

Устойчивое равновесное состояние термодинамических систем характеризуется следующими общими условиями:

1) неизменностью равновесного состояния системы при сохранении внешних условий;

2) подвижностью равновесия (самопроизвольным восстановлением равновесия после прекращения внешнего воздействия, вызвавшего незначительное отклонение системы от положения равновесия);

3) динамическим характером равновесия, т.е. установлением и сохранением его вследствие равенства скоростей прямого и обратного процессов;

4) возможностью подхода к состоянию равновесия с двух противоположных сторон;

5) минимальным значением изменения изобарно-изотермического или изохорно-изотермического потенциалов ( ). Выражением этих условий является закон действия масс (константы равновесия).

Для химической реакции в общем виде:

,

протекающей в газовой фазе в изобарно-изотермических условиях, константа равновесия равна:

         ; ; ; ,           (40)

где:  - равновесные значения концентраций веществ (С_i, моль/л), парциальных давлений (P_i, кПа), мольных долей (N_i), числа молей соответственно (ν_i, моль).

Константа равновесия, выраженная через парциальные давления компонентов газовой смеси, связана с константами  соотношениями:

,                                (41)

где: Р – общее давление в системе;  - изменение числа молей газа в реакции, ; - сумма числа молей компонентов в равновесной газовой смеси, .

Параметры твердых и жидких веществ, участвующих в реакции наряду с газами, не входят в выражение для констант равновесия (их активности равны единице) и поэтому не принимаются в расчет при вычислении  и .

По значению константы равновесия реакции можно рассчитать состав равновесной смеси, т.е. определить максимально возможный, или теоретический, выход продукта. Константу равновесия можно выразить через равновесную степень превращения (α) одного из веществ, участвующих в реакции. Степень превращения исходного вещества можно рассчитать по формуле: . В соответствии с уравнением химической реакции можно выразить равновесный состав смеси, используя степень превращения.

Например, для реакции  за исходный состав можно принять 1 моль азота и, соответственно, 3 моль водорода. Если степень превращения азота обозначить через α, то равновесный состав газовой смеси можно представить следующим образом:

1. (1-α) моль N₂

2. (3-3α) моль Н₂

3. 2α моль NH₃

.

 Сумма молей в равновесной газовой смеси (Σν) будет равна:

Σν = (1 – α) + (3 − 3α) + 2α= 4 –2 α.

Изменение числа молей в реакции будет равно .

 

, , .

В основе термодинамического расчета констант равновесия и равновесных выходов продуктов лежит уравнение изотермы химической реакции Вант-Гоффа:

                                             (42)

где:  - произвольные парциальные давления  начальных веществ и продуктов реакции.

Для стандартного состояния системы, уравнения химического сродства имеют вид:          .                                                                (43)

Зависимость константы равновесия от температуры выражается уравнением изобары  Вант-Гоффа в дифференциальном виде:

                                      .                                                  (44)

 Допуская, что в небольшом интервале температур ; , для расчета константы равновесия можно применить уравнение , где: К_Р,1 и К_Р,2 – константы равновесия при температурах Т₁ и Т₂, соответственно.  Если подставить в последнее уравнение , то получим выражение, , которое с учетом уравнения изотермы (уравнение химического сродства)   принимает вид:

  .                                             (45)

Значения  рассчитывают по закону Гесса.

     

Примеры решения типовых задач

Пример 1. Константа скорости реакции омыления этилацетата (вещество А) едким натром (вещество В) при 298 К равна 2,38, концентрации веществ выражены в моль/л, а время – в минутах. Вычислите время, необходимое для омыления 50% этилацетата (α_А), если смешать 1 л раствора эфира концентрацией 0,05 моль/л с 1 л раствора NaOH концентрацией 0,05 моль/л. Молекулярность и порядок реакции совпадают.

Дано: Т = 298 К  k = 2,38 моль/л∙мин С′0, А = 0,05 моль/л С′0, В = 0,05 моль/л ΔСА = αА αА = 0,50 ∙ С0,А Сτ = С0,А– ΔСА

Решение. Уравнение процесса: А + В = D + R, реакция является бимолекулярной, а, следовательно, второго порядка. Концентрации эфира и щелочи равны, поэтому используем кинетическое уравнение:  или . Так как объем смеси равен 2 л, то за счет разбавления начальная концентрация эфира будет равна:           С0,А= С′0, А/2= 0,025 моль/л, а так как прошло омыление 50% эфира, то к моменту времени τ концентрация эфира стала равна 0,0125 моль/л. Время реакции будет определяться: мин.

Найти: τ ?

Ответ: τ = 16,8 мин.

 

 

Пример 2. Реакция первого порядка А₂ → А + А проходит на 30 % за 35 мин. Рассчитайте скорость реакции (в моль/л∙мин) при исходной концентрации реагирующего вещества 0,01 моль/л в начале реакции и по истечении 35 мин.

       

Дано: n = 1 С0,А = 0,01 моль/л ΔСА=0,3∙ С0,А=0,003моль/л τ = 35 мин	Решение. Используя кинетическое уравнение первого порядка, находим константу скорости или нулевую скорость процесса при τ = 0: 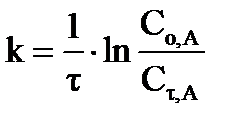, где Сτ,А = С0,А– ΔСА, Сτ,А=0,01–0,003=0,007 моль/л. = 1,02∙10-2 моль/л∙мин. Скорость по истечении 35 мин рассчитываем по уравнению: υτ = k∙ Сτ,А ,  υ35 = 1,02∙10-2∙0,007 = 0,71∙10-4 моль/л∙мин.
Найти: k, υ35 ?	Ответ: k = 1,02∙10-2 моль/л∙мин;        υ35 = 0,71∙10-4 моль/л∙мин.

 

Пример 3. Пример 2. Для химической реакции А  В константа скорости реакции равна 0,5 моль/л∙час, начальная концентрация вещества А равна 1 моль/л. Вычислите степень превращения ( ) вещества А за 1 час, если реакция идет по: а) первому порядку; б) по второму порядку. Как зависит степень превращения от порядка реакции?

Дано: k =0,5 С0,А=1   а) n =1 б) n=2 τ = 1 час	Решение. Степень превращения (α) это изменение концентрации реагирующего вещества: αА = ΔСА = С0,А– Сτ,А. а) Для реакции первого порядка, согласно уравнению  , находим: ; моль/л. б) Для реакции второго порядка, используем уравнение , ,  моль/л.
Найти: αа, αб?	Ответ:  моль/л,  моль/л; чем выше порядок реакции, тем меньше степень превращения, тем медленнее идет реакция.

 

Пример 4. Константа скорости превращения свекловичного сахара меняется с температурой следующим образом:

Т, К……………………..293             303            323

……….….2,758         10,980     137,400.

Вычислите температурный коэффициент превращения сахара для каждого температурного интервала и средний температурный коэффициент в пределах от 293 до 323 К.

 

Дано: Т1=293К Т2=303К Т3=323К k1=2,758∙10-4 мин-1 k2=10,980∙10-4мин-1 k3=137,40∙10-4мин-1	Решение. Температурный коэффициент скорости реакции (γ) определяется по правилу Вант-Гоффа: . а) Для температурного интервала 293К ÷ 303К  , . б) Для температурного интервала 303К ÷ 323К , . в) Для температурного интервала 293К ÷ 323К  , . .
Найти: γ1, γ2, γ3 ?         γ ср ?	Ответ: γ ср = 3,734 ≈ 4.

 Пример 5. Определите энергию активации реакции:

,

если константа скорости с температурой меняется следующим образом:

Т, К……………………...293,2          313,2            333,2

…….9,60               18,16            39,96.

Дано: Т1=293,2 К Т2=313,2 К Т3=333,2 К k1=2,758∙10-3 k2=10,980∙10-3   k3=137,40∙10-3	Решение. Находим энергию активации (ЕА, в кДж/моль) по уравнению: . Для температурного интервала от 293,2 до 313,2 К ; для интервала температур от 313,2 до 333,2 К  ; для интервала температур от 293,2 до 333,2 К ; .
Найти: ЕА,сред. ?	Ответ: ЕА,сред. =29,17 кДж/моль.

Пример 6. Константа равновесия реакции  H_2(Г)+I_2(Г) =2 HI_(Г) при 693 К . Вычислите массу образующегося иодида водорода, если в сосуд вместимостью 1 л введено 846 г йода и 21,2 г водорода.

Дано: V = 1л m(I2) = 846 г m(H2) = 21,2 г

Решение. Уравнение процесса:  H2(Г)+I2(Г) =2 HI(Г). Определим количество молей исходных веществ по формуле   (ν = m/M):      ν0(H2) = 21,2/2 = 0,0106 моль,                          ν0(I2) = 846/254 = 0,0033 моль. Число молей иодида водорода в исходном состоянии равно нулю (ν0(HI)=0). Изменение числа молей к моменту равновесия йода и водорода (Δν(H2)= Δν(I2)= х) будет одинаковым (исходя из уравнения процесса), а равновесное число молей HI будет определяться удвоенным изменением числа молей H2 или I2: νравн.(HI)=2∙Δν=2х. Равновесное число молей остальных  веществ в системе составит: νравн.(H2)= ν0(H2) –х =(10,6∙10-3 – х ) моль,  νравн.(I2)= ν0(I2) –х =(3,33∙10-3 – х) моль. Находим: , Решение этого уравнения дает . Откуда , , . Первый корень уравнения не имеет физического смысла, так как величина  не может быть больше ν0(H2), т.е. . Следовательно, равновесное количество полученного йодистого водорода будет составлять: .

Найти: m(HI)?

Ответ: m(HI) = 0,82 г.

 

Пример 9. В закрытый сосуд вместимостью 0,05  введено 10 моль вещества А и 1 моль вещества В. В результате реакции 2A+B=D установилось равновесие с общим давлением в системе 485 кПа. Вычислите равновесные количества всех веществ в системе при 298 К. Чему равно значение  при этой температуре? Система подчиняется законам идеального газа.

 

Дано: V = 0,05 м3 ν0(А) = 10 моль ν0(В) = 1 моль ν0(D) = 0 моль Робщ = 485 кПа Т=298 К

Решение. Уравнение процесса: 2A(Г)+B(Г)=D(Г). Если обозначить количество превращенных молей вещества В через х то: Δν(В)=х, Δν(А)=2х, Δν(D)=х (согласно уравнению реакции). Равновесное число молей  веществ в системе можно рассчитать: νравн.=ν0 –Δν;  νравн.(А)=10–2х моль, νравн.(В)=1–х моль, νравн.(D)=х моль. Сумма молей в равновесной системе составит:  . По уравнению Менделеева-Клапейрона  находим значение х: , 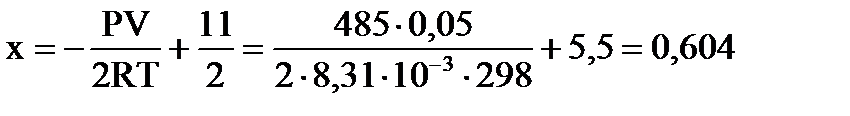моль. Равновесные количества веществ в системе составят: νравн.(А) =10–2∙0,604=8,792 моль, νравн.(В)=1–0,604=0,396 моль,    νравн.(D)=0,604 моль. Константы равновесия рассчитываем по уравнениям:   Изменение числа молей газов в результате процесса  по уравнению составляет Δν = 1–2–1 = –2 моль, .

Найти: νравн.(А), νравн.(В), νравн.(D), Кр, Кс ?

Ответ: νравн.(А)=8,792 моль, νравн.(В)= 0,396 моль, νравн.(D)= 0,604 моль, Кс=48,42, Кр=7,89∙10−6.

 

Контрольные вопросы и задания

Вариант 1

1.Реакция при 20 С завершается за 60 с. Сколько для этого потребуется времени при 40 С, если энергия активации равна 33,4 кДж/моль?

2. В каком направлении сместится равновесие в системе N_2(Г) + 3H_2(Г) ↔ 2NH_3(Г), при условии, что ΔH⁰_хр <0: а) при увеличении концентрации N₂; б) при увеличении концентрации Н₂; в) при повышении температуры; г) при уменьшении давления?

3. Как следует изменить температуру, чтобы скорость реакции увеличилась в 8 раз (γ=2)?

4.  В системе 2NO_(г)+ O_{2 (г)}=  2NO_{2 (г)} равновесные концентрации веществ равны [NO]=0,2 моль/дм , [O₂]=0,3 моль/дм , [NO₂]=0,4 моль/дм . Укажите преимущественное направление реакции.

Вариант 2

1. Приведите выражение закона действия масс для реакции 2NO_(г)+ Сl_2(г) = 2NOCl_(г), укажите общий порядок реакции. Как изменится скорость реакции при увеличении давления в 4 раза; понижении C_NO в 50 раз?

2. Реакция синтеза метанола протекает по уравнению:                                       СО_(Г)+2Н_2(Г) ↔СН₃ОН_(Г),  кДж/моль. Как надо изменить температуру, давление и концентрацию, чтобы сместить равновесие в сторону образования метанол?

3. При 633 К и 101,33 кПа степень диссоциации HI равна 20%. Рассчитайте стандартное сродство газообразного иода к водороду.

4. Энергия активации реакции разложения некоторого вещества равна 75 кДж/моль, а обратной реакции – 265 кДж/моль. Рассчитайте температурный коэффициент скорости прямой реакции в интервале температур: 60⁰ – 80⁰С и стандартную энтальпию реакции.

 

Вариант 3

1.  Определите, как изменится скорость прямой реакции

2СО_(Г)+ О_2(Г) = 2СО_2(Г), если общее давление в системе увеличить в 4 раза.

2. Для реакции разложения HI константа скорости (k, мин⁻¹) при 553 К равна , а при 573 К она равна . Определите энергию активации, константу скорости реакции при 563 К и температурный коэффициент скорости реакции.

3. При 693 К водород и йод находятся в закрытом сосуде. В исходном состоянии системы парциальные давления  и  Па. Равновесное парциальное давление HI  Па. Вычислите равновесные парциальные давления водорода и йода и константу равновесия.

4. При 633 К и 101,33 кПа степень диссоциации HI равна 20%. Рассчитайте стандартное сродство газообразного йода к водороду.

 

Вариант 4

1.  Как следует изменить температуру, чтобы скорость реакции увеличилась в 4 раза (γ=4)?

2. Как изменится скорость реакции при повышении температуры с 600 до 650 К, если энергия активации равна 26,6 кДж/моль?

3. Процесс получения хлора окислением хлороводорода протекает по уравнению реакции  4HCl_(Г)+O_2(Г)=2H₂O_(Г)+2Cl_2(Г). При смешении 1,000 моль HCl с 0,480 моль  образуется 0,402 моль хлора. Вычислите , если общее давление в системе  и температура 298 К.

4. Степень диссоциации 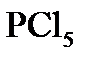 при 473 К и 101,33 кПа равна 0,485, а при температуре 523 К и том же давлении она равна 0,800. Рассчитайте средний тепловой эффект реакции  при P = const в интервале температур от 473 до 523 К.

Вариант 5

1. Температурный коэффициент скорости реакции равен 2,0. Как изменится ее скорость: а) при охлаждении реакционной смеси от 50⁰ до 30⁰ С; б) при повышении температуры на 60⁰ С?

2. Запишите выражение закона действия масс для реакции , укажите общий порядок реакции. Как изменится скорость реакции при увеличении давления в 4 раза; понижении парциального давления водорода  в 50 раз?

3. Определите константу равновесия реакции   при 700 К, если при 500 К  (давление выражено в Па), а тепловой эффект в этом диапазоне температур  равен –99,48 кДж.

4. Для реакции разложения  в водном растворе константа скорости  при 283 К равна , а при 303 К равна . Определите энергию активации реакции.

 

Вариант 6

1. При 298 К некоторая реакция заканчивается за 2,5 часа. Принимая температурный коэффициент равным 3, рассчитайте, при какой температуре реакция закончится за 20 минут.

2. Определите температуру, при которой давление  над  будет 100 кПа, если при 1035 К давление равно 13,332 кПа. Тепловой эффект реакции  при 1035 К равен 167,91 кДж/моль. Считайте, что в данном температурном интервале тепловой эффект реакции не зависит от температуры.

3. При 823 К и давлении 101,33 кПа (1 атм) степень диссоциации фосгена на оксид углерода (II) и хлор равна 77%. Определите  и .

4. Две реакции одинакового порядка имеют равные предэспоненциальные множители, но их энергии активации различаются на 41,9 кДж/моль. Рассчитайте соотношения констант скоростей этих реакций при 600К.

 

Вариант 7

1. Вычислите температурный коэффициент скорости реакции, если понижение температуры на 40 К вызывает уменьшение скорости реакции в 140 раз.

2. Константа равновесия реакции  при 673 К  (давление измерено в Па). После смешения по 1 моль водорода и азота к моменту равновесия 10% азота превратилось в аммиак. Рассчитайте значение общего давления в системе при этом?

3. Вещество А смешано в равных количествах с веществами В и D (С₀(А,В,D) = 1 моль/л). По истечении 1000 секунд половина вещества А прореагировала. Определите количество вещества А, которое остается по истечении 2000 секунд, если данная реакция первого порядка.

4. При повышении температуры от 20⁰ до 40⁰ С скорость реакции увеличилась в 6 раз. Вычислите температурный коэффициент и энергию активации реакции.

Вариант 8

1. При 140⁰ С реакция заканчивается за 30 с. Сколько времени потребуется для данной реакции при 20⁰ С, если γ=2?

2. При 323 К и давлении 34,85 кПа степень диссоциации  равна 63%. Определите значение констант равновесия  и  для реакции  в данных условиях.

3. Равновесие в системе, в которой протекает реакция , устанавливается при 500 К и общем давлении 100 кПа. Равновесное парциальное давление  равно 64 кПа (изначально присутствовал только ). Рассчитайте стандартное сродство этого процесса при 500 К. При каком общем давлении парциальное давление  будет равно 10 кПа?

4. При определенной температуре 0,01 моль/л раствор уксусно-этилового эфира омыляется 0,002 молярным раствором щелочи за 23 мин на 10%. Через сколько минут он будет омылен до такой же степени 0,005 молярным раствором щелочи? Данная реакция является реакцией второго порядка, а щелочь диссоциирована полностью.

Вариант 9

1. При повышении температуры на 20⁰ С скорость реакции возросла в 9 раз. Чему равен температурный коэффициент этой реакции и во сколько раз увеличится ее скорость при повышении температуры с 20⁰ до 100⁰ С?

 2. Реакция при 20 ⁰С завершается за 60 с. Сколько для этого потребуется времени при 40⁰С, если энергия активации равна 33,4 кДж/моль?

3. Константа равновесия реакции N_2(Г)+3H_2(Г)↔2NH_3(Г) при 673 К  (давление измерено в Па). После смешения по 1 моль водорода и азота к моменту равновесия 10% азота превратилось в аммиак. Рассчитайте значение общего давления в системе при этом?

4. Вычислите степень превращения ( ) исходных веществ реакции

A+4B=D и равновесный выход (Х) конечного продукта реакции D, если начальные количества исходных веществ:  моль,  моль. При достижении равновесия количества веществ имели значения: ,  моль. Рассчитайте константу равновесия , если объем реакционного сосуда равен 50 л.

 

Вариант 10

1. Температурный коэффициент скорости реакции равен 3. Как изменится скорость реакции при уменьшении температуры с 125⁰ до 55⁰ С?

2. Как изменится скорость реакции при повышении температуру до 50⁰С, если энергия активации равна 125,5 кДж/моль?

3. Определите константу равновесия реакции   при 700 К, если при 500 К  (давление выражено в Па), а тепловой эффект в этом диапазоне температур  равен –99,48 кДж.

4. Константа равновесия реакции  при 693К . Вычислите массу образующегося иодида водорода, если в сосуд вместимостью 1 л введено 846 г иода и 21,2 г водорода.

Вариант 11

1. При повышении температуры на 20⁰ С скорость реакции возросла в 9 раз. Чему равен температурный коэффициент этой реакции и во сколько раз увеличится ее скорость при повышении температуры с 20⁰ до 100⁰ С?

2. При 823 К и давлении 101,33 кПа (1 атм) степень диссоциации фосгена на оксид углерода (II) и хлор равна 77%. Определите  и .

3. Вычислите температурный коэффициент скорости реакции гидролиза сахарозы в кислом водном растворе в температурном интервале от 10⁰С до 50⁰ С, если энергия активации реакции равна Е_а = 107 кДж/моль.

4. Равновесие в системе, в которой протекает реакция , устанавливается при 500 К и общем давлении 100 кПа. Равновесное парциальное давление  равно 64 кПа (изначально присутствовал только ). Рассчитайте стандартное сродство этого процесса при 500 К. При каком общем давлении парциальное давление  будет равно 10 кПа?

 

Вариант 12

1. Температурный коэффициент скорости реакции равен 2,5. Как изменится ее скорость: а) при охлаждении реакционной смеси от 50⁰ до 30⁰ С; б) при повышении температуры на 60⁰ С?

2. В закрытый сосуд вместимостью 0,01  введено 10 моль вещества А и 2 моль вещества В. В результате реакции 2A+B=D установилось равновесие с общим давлением в системе 400 кПа. Вычислите равновесные количества всех веществ в системе при 298 К. Чему равно значение  при этой температуре? Система подчиняется законам идеального газа.

3. Константа равновесия реакции  при 633 К равна 61,6, а при 718 К она равна 41,7. Определите среднее значение теплового эффекта реакции и сродство при 718 К.

4. После удаления катализатора из системы, энергия активации реакции возросла на 40 кДж/моль при температуре 37⁰С. Как изменилась скорость реакции?

Раздел 5

                                                       Растворы

    Растворы – многокомпонентные системы. Компонент, который в данных условиях находится в том же агрегатном состоянии, что и образующийся раствор, считают растворителем, остальные составляющие раствора – растворенными веществами, растворённых веществ может быть одно или несколько.

Свойства любого водного раствора зависят от размера частиц растворенного вещества и от их реакции на действие силы тяжести. По этим признакам различают три типа растворов: истинные растворы, коллоидные растворы и суспензии или эмульсии.  В истинных растворах размеры частиц растворенного вещества  сравнимы с размерами молекул растворителя (воды). Истинный раствор является гомогенной  системой, практически состоящей из одной фазы. Частицы истинного раствора не разделяются под действием силы тяжести. Истинными растворами организма являются, например, растворы солей, моносахаридов.

 

5.1. Способы выражения содержания растворенного вещества в растворе, классификация истинных растворов

1. Массовая доля ( )  − процентное отношение массы растворенного вещества (m_в) к общей массе раствора (m_р-р):

 = m_в/ m_р-р, или процентная концентрация (С, %):

                                                         С = ∙100 %.                                       (46)

2. Мольная доля (N_i) – отношение количества молей данного компонента раствора (ν_i) к сумме количества молей всех веществ в растворе:

                                        (Σν): N_i = ν_i/ Σν.                                                   (47)

3. Молярная концентрация (С_м, моль/л или М) – отношение количества растворенного вещества (ν_в) к объему раствора (V_р, л):

        С_м = ν_в/ V_р или С_м = m_в/(М_в∙ V_р),                                                (48)

где М_в – мольная масса вещества.

4. Эквивалентная концентрация или нормальность (С_н, моль/л) – отношение числа эквивалентов (n_э = m_в /m_э) растворенного вещества к объему раствора (V_р, л), где m_э – масса эквивалента вещества:

    С_н = n_э/ V_р или С_н = m_в/(m_э∙ V_р).                                                        (49)

5. Моляльная концентрация или моляльность (С_m, моль/кг растворителя) – отношение количества растворенного вещества (ν_в) к массе растворителя (m_р-ль):

   С_m = ν_в/m_р-ль, или С_m = m_в∙10³/( М_в∙ m_р-ль).                                               (50)

Насыщенный раствор – раствор вещества, находящийся в равновесии при данной температуре с твердой фазой растворяемого вещества. Концентрация насыщенного раствора данного вещества является величиной постоянной при данной температуре и определяется растворимостью вещества. Коэффициент растворимости это масса вещества, растворяющегося в 100 г растворителя с образованием насыщенного раствора в данных условиях.

 

Классификация истинных растворов

Растворы электролитов

Растворы неэлектролитов, растворяемое вещество в растворе находится в виде электронейтральных частиц (молекул)

Растворы слабых электролитов, веществ,         Растворы сильных электролитов, веществ,  степень диссоциации которых 0˂α˂1                степень диссоциации которых α→1

Водные, растворителем является вода

Органические, растворитель – любая органическая жидкость (С6Н6, СО(СН3)2, С2Н5ОН и т.д.)

Жидкие

РАСТВОРЫ

Твердые – сплавы: твердые растворы замещения и внедрения

 

 

 

5.2. Коллигативные свойства растворов неэлектролитов

Свойства растворов, количественное выражение которых зависит только от числа частиц растворенного вещества и от количества растворителя называются коллигативными.

I .  Одним из таких свойств является функциональная зависимость понижения давления насыщенного пара растворителя над раствором нелетучего вещества от количества вещества в растворе (закон Рауля).

Относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле растворенного вещества ( N_B ):

                                   (Р₀–Р)/Р₀ = N_{B ,}                                                                                         (51)

где: Р₀, Р – давления насыщенного пара растворителя над чистым растворителем (А) и давления насыщенного пара растворителя над раствором вещества (В), соответственно.

Закона Рауля имеет два следствия:

1) понижение температуры замерзания раствора (ΔТ_зам) по сравнению с температурой замерзания чистого растворителя пропорционально моляльной концентрации растворенного вещества (В)

                   ΔТ_зам = К∙ С_m   или                          (52, 53)

где: К – криоскопическая постоянная (численное значение определяется природой растворителя, см. в справочнике); m_{B ,} m_A – масса растворённого вещества и растворителя, соотвенственно; М_В – мольная масса растворённого вещества, 10³– 1000 г растворителя.

2) повышение температуры кипения раствора (ΔТ_кип) по сравнению с температурой кипения чистого растворителя пропорционально моляльной концентрации растворенного вещества (В): 

        ΔТ_кип = Е ∙ С_m  или                             (54, 55)

где: Е – эбуллиоскопическая постоянная (численное значение определяется природой растворителя, см. в справочнике).

Оба следствия используются для экспериментального определения молярных масс растворённых веществ.

 II . Явление осмоса. Мембраны имеющие строго фиксированные, но очень малые размеры пор, могут пропускать через себя только низкомолекулярные вещества (например, воду). Такие мембраны называются полупроницаемые. Если система состоит из двух растворов одного и того же вещества, но разной концентрации и между ними поместить полупроницаемую мембрану, то в такой системе наблюдается явление, называемое осмосом.

Осмос – это самопроизвольное явление односторонней диффузии растворителя через полупроницаемую мембрану.

Осмос приводит к увеличению объема той части системы, в которой был раствор с повышенной концентрацией. В результате поднятия уровня в этой части системы, на мембране возникает избыточное гидростатическое давление, которое называется осмотическим (π, кПа). Осмотическое давление зависит только от концентрации вещества (С_м) и от температуры (Т), но не зависит ни от природы растворенного вещества, ни от природы растворителя. Экспериментально осмотическое давление в системе измеряется приборами – осмометрами. Функциональная зависимость осмотического давления от концентрации вещества выражается уравнением Вант-Гоффа:

                  π = С_м(В)∙RT или  π = m_В∙RT /(М_В∙ V_р),                                 (56,57)                                

где: m_B, М_В – масса и молярная масса растворенного вещества; V_р – объем раствора.

Экспериментально определив осмотическое давление раствора данной концентрации, по уравнению Вант-Гоффа можно рассчитать молярную массу растворенного вещества.

5.3. Растворы электролитов

Электролитами называются вещества, молекулы которых в растворе или в расплаве распадаются (диссоциируют) на ионы. Диссоциация веществ происходить с разной степенью. Количественной характеристикой данного процесса является степень диссоциации (α), значение которой может быть: 0≤ α ≤1.

 5.3.1.  Растворы слабых электролитов, их количественные характеристики.

1) Константа диссоциации.

Процесс диссоциации слабого электролита является обратимым и, следовательно, равновесным. Процесс диссоциации бинарного электролита (в общем виде) можно записать: АВ ↔ А⁺ + В^– . Любой равновесный процесс характеризуется константой равновесия, т.к. в данном случае это процесс диссоциации, то и константа называется константой диссоциации (К_Д). Для данного процесса выражение константы равновесия имеет вид: = , где: [A⁺] и [B^–] – равновесные концентрации ионов; [АВ] – равновесная концентрация молекул не распавшихся на ионы (недиссоциированных). Численное значение константы диссоциации, как константы равновесия, определяется только природой вещества и температурой. Для слабых электролитов константы диссоциации определены экспериментально при стандартной температуре и их значение можно найти в справочной литературе. Данная количественная характеристика (К_Д) от концентрации вещества в растворе не зависит.

2) Второй количественной характеристикой данного процесса является степень диссоциации: α = С_Д/С_м, где: С_Д – количество вещества претерпевшего диссоциацию, С_м – исходная молярная концентрация вещества. Значение степени диссоциации зависит от концентрации, чем больше концентрация вещества, тем меньше его степень диссоциации

Для бинарного электролита АВ равновесные концентрации ионов  будут равны и каждая будет определяться исходной молярной концентрацией и степенью диссоциации:  [A⁺] = [B^–] = α∙ С_м , а концентрация недиссоциированных молекул АВ определяется: [АВ] = (1– α) ∙ С_м. Если в выражении закона действующих масс (т.е. в выражении константы равновесия) равновесные концентрации заменить их значением через степень диссоциации и исходную концентрацию, то можно получить выражение закона разбавления Оствальда:

                      = ;  = .                                (58,59)                                                                                                                                            

Для слабых электролитов и концентрациях С_м ˂ 0,02 моль/л значение (1– α)→1. Зная концентрацию вещества и его природу, используя закон Оствальда можно рассчитать степень диссоциации: α =  , К_Д см. в справочнике.

  5.3.2 .Ионное произведение воды. Водородный и гидроксильный показатели

Примером очень слабого электролита является жидкая вода.  Молекула воды является ярко выраженным диполем с большим значением дипольного момента  (μ = 6,13∙10^-30 Кл∙м).          

Процесс диссоциации:  Причем, равновесие диссоциации очень сильно сдвинуто в сторону молекулярной формы (влево), поэтому можно условно считать концентрацию молекулярной формы воды величиной постоянной и равной: С_м= [Н₂О] = m(Н₂О)/(М(Н₂О)∙ V_р), где: V_р – объем воды равный 1 л, m(Н₂О) – масса 1л воды (1000 г), следовательно, [Н₂О] =1000/(18∙1) = 55,5(5) моль/л.

     Константа равновесия или константа диссоциации воды имеет вид:

 К_Д =  Если константу диссоциации умножить на равновесную концентрацию молекулярной воды, то получим новую постоянную, которая называется ионным произведением воды:  К_ѡ = К_Д∙[Н₂О] = [H⁺]∙[OH^-]. Экспериментально определено значение ионного произведения воды: К_ѡ = 1,08∙10^-14 или в стандартных условиях:  К_ѡ = 10^-14, при этом  для воды, не содержащей примесей, концентрации ионов водорода и гидроксила будут равными:  [Н⁺] = [ОН^-] = 10^-7 моль/л.

Для количественной характеристики кислотности или щелочности любого водного раствора используются водородный (рН) или гидроксильный (pOH) показатели. Это значение отрицательного логарифма концентрации соответствующего иона:

                           рН = ‒ lg[H⁺];                                                                         (60)

                           pOH = ‒ lg[OH^‒];                                                                (61)

                            рН + рОН = 14.                                                                  (62)

Среда  водной системы может быть охарактеризована по значениям pH и pOH:

 а) нейтральная среда при [H⁺] = [OH^‒] = 10^-7 моль/л, рН = 7, рОН = 7;

б) кислая среда при [H⁺] >[OH^‒], [H⁺] > 10^-7 моль/л,  рН ˂ 7, рОН > 7;

в) щелочная среда при [H⁺] ˂[OH^‒], [H⁺] ˂ 10^-7 моль/л, рН > 7, рОН ˂ 7.

Все процессы взаимодействия воды с различными веществами сводятся к двум основным типам: а) процессы гидратации; б) процессы гидролиза.

   5.3.3. Процессы гидратации и гидролиза. Количественные характеристики гидролиза

      Процесс гидратации - это взаимодействие высоко полярных молекул воды с молекулами или ионами  веществ, входящих в контакт с водой.  Молекула воды, имеющая высокие эффективные заряды атомов, является ярко выраженным диполем и вступает в различные виды диполь-дипольного и диполь-ионного взаимодействия. Результатом такого взаимодействия являются соединения называемые гидратами. Процесс гидратации сопровождает растворение любого вещества в воде, например, растворение ионных кристаллов NaCl:

NaCl + n Н₂О → Na⁺∙xH₂O + Cl⁻ ∙yH₂O,  при этом вокруг каждого вышедшего из кристаллической решетки иона возникает оболочка из молекул воды (гидратная шуба), а возникшие соединения (Na⁺∙xH₂O и Cl⁻ ∙yH₂O) называются гидратами,

где x и y – степени гидратации соответствующих ионов.

Образование гидратных оболочек происходит и при растворении в воде неэлектролитов, молекулы которых слабо полярны или обладают наведенным диполем. Гидраты, как правило, нестойкие системы и разлагаются при выпаривании растворов. В некоторых случаях энергия гидратации очень высока, а гидраты прочны настолько, что при упаривании раствора вода входит в состав кристаллов вещества и называется кристаллизационной. Полученные при этом вещества называют кристаллогидратами, которые по существу являются комплексными соединениями. Состав кристаллогидратов описывается брутто формулой с указанием количества кристаллизационной воды, приходящейся на 1 моль основного соединения (например, ВаCl₂∙2Н₂О; Na₂SO₄∙10Н₂О; CrCl₃∙6Н₂О).

Степень гидратации различных ионов и молекул неодинакова и зависит от размеров частиц и величины их заряда. Чем больше заряд и меньше размеры иона, то есть выше удельная плотность заряда, тем больше степень гидратации. Ион Li⁺ гидратирован больше, так как удельная плотность заряда у него выше, чем у ионов К⁺. Недиссоциированные молекулы также в той или иной степени гидратированы, их гидратная оболочка возникает только вокруг полярных групп и потому может быть не сплошной.

 Процессы гидролиза  – это реакции обменного разложения между молекулами воды и соответствующего соединения. Гидролиз солей является результатом поляризационного взаимодействия ионов электролита с молекулами воды гидратной оболочки. Характер и степень диссоциации молекул воды гидратной оболочки зависят от природы гидролизующихся ионов: чем сильнее поляризующее действие иона, тем выше степень гидролиза. При этом возможны следующие варианты:

1) если соединение при ионизации в растворе образует слабо поляризующие катионы (катионы щелочных и щелочноземельных металлов, Li⁺, Ва²⁺ и т.д. ) и слабо поляризующие анионы (анионы сильных кислот, Cl^-, NO₃ ^– и т.д.) гидролиз практически не протекает, и рН среды не изменяется;

2) если соединение при ионизации в растворе образует средне поляризующие катионы и слабо поляризующие анионы (соли слабых оснований и сильных кислот), то идет гидролиз по катиону, сопровождающийся появлением избытка ионов водорода, при этом значение рН становится меньше 7:

а) СuCl ₂ ó Cu²⁺ + 2Cl⁻ ,

б) ,

в) Cl⁻ ∙yH₂O+Н₂О →реакция не протекает;

в молекулярной форме: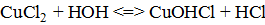

3) При диссоциации соединения на слабо поляризующие катионы средне поляризующие анионы (соли слабых кислот и сильных оснований), гидролиз идет по соли аниону и в системе создается щелочная среда:

а) Na₂ CО₃ ó 2Na⁺ + CО₃^2- ,

б) Na⁺∙xH₂O + H₂O→реакция не протекает,

в) ;

в молекулярной форме:

4) Если соединение при ионизации образует средне поляризующие катионы и анионы (соль образованна слабым основанием и слабой кислотой), гидролиз происходит и по катиону, и по аниону. При этом идет образование слабых оснований и слабых кислот:

.

Реакция среды в этом случае зависит от относительной силы образовавшихся продуктов: кислоты и основания. Данный случай является примером полного гидролиза, а соль относится к солям, необратимо разлагаемым водой.

5) Гидролизу подвергаются соединения ковалентного типа химической связи, которые в воде претерпевают необратимое гидролитическое разложение. Данный процесс протекает через промежуточные стадии комплексообразования и может включать окислительно-восстановительные этапы:

 

Количественные характеристики гидролиза

Количественно гидролиз характеризуется степенью и константой гидролиза.

Степень гидролиза (b) определяется отношением числа гидролизованных ионов соли  к общему числу ионов данного вида:

             ,                                                                  (63)

где: K_гидр. - константа гидролиза; C_м – молярная концентрация соли.

Степень гидролиза увеличивается при повышении температуры и разбавлении раствора, так как уменьшается концентрация соли (C).

В формулу (63) входит константа гидролиза, которая также характеризует способность соли к гидролизу. Чем больше K_гидр., тем сильнее соль подвергается гидролизу.

Константа гидролиза связана с константой диссоциации слабого электролита соотношением:

                                                               (64)

Чем слабее электролит, ион которого подвергается гидролизу, (чем меньше его К _{диссоциации} ) тем больше константа гидролиза (K_гидр)..

Знание константы и степени гидролиза дают возможность рассчитать концентрацию [H⁺] и определить величину pH раствора:

а) Если соль образована слабой кислотой, то концентрация накапливающихся ионов OH^‑ определяется по формуле:

 , где C_М – молярная концентрация соли, ,

отсюда:

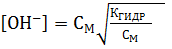= ,      тогда: = .

Подставим в эту формулу выражение K_гидр. (64), получим:

                                                              (65)

 

 

б) Аналогично для соли, образованной слабым основанием, получим:

                                                         (66)

в) Если соль образована слабой кислотой и слабым основанием, то

                                                        (67)

pH раствора в этом случае не зависит от концентрации соли, а определяется силой кислоты и основания, образовавших данную соль.

5.3.4. Произведение растворимости. (Константа растворимости)

К очень слабым электролитам относятся все плохо и трудно растворимые в воде электролиты. При растворении твердых веществ в воде часто пользуются понятием растворимости, мерой которой служит содержание данного вещества в насыщенном растворе. Количественной мерой процесса растворения таких веществ в воде является произведение растворимости (ПР,илиКР). Значение данной величины зависит только от природы вещества и температуры, но не зависит от присутствия в системе каких либо других ионов.  В насыщенном растворе малорастворимого электролита произведение концентрации его ионов есть величина постоянная при данной температуре. Если произведение концентрации ионов> ПР, то выпадает осадок, если произведение концентраций ионов < ПР, то осадок растворяется.

Труднорастворимый электролит характеризуется равновесием между твердой фазой и ионами, перешедшими в раствор. Пример:

BaSO₄ « Ba²⁺ + SO₄^2‑

Данный равновесный процесс подчиняется законам равновесия и описывается константой равновесия: , .

Концентрация твердой фазы является величиной постоянной, поэтому:

K·const = [Ba²⁺]·[SO₄^2‑] - эта величина называется произведением растворимости (ПР).

Если формульная единица трудно растворимого соединения выражается формулой Kt_mAn_{n ,} то его процесс диссоциация имеет вид:

                        Kt_mAn_n « mKtⁿ⁺ + n An^m-

Тогда выражение ПР имеет вид:

                                  ПР = [Ktⁿ⁺]^m · [An^m-]ⁿ .                                                      (68)

 Например, если имеется осадок CaCO₃, это означает, что [Ca²⁺]·[CO₃^2‑] > ПР (CaCO₃). Чтобы осадок растворить, надо уменьшить концентрацию одного из этих ионов, например:

CO₃^2‑ + 2H⁺ = H₂O + CO₂­.

Таким образом можно добиться того, что [Ca²⁺]·[CO₃^2‑] станет меньше ПР этой соли и осадок растворится. Значение ПР для таких веществ см. в справочнике.

 

          5.3.5. Растворы сильных электролитов.

1) Активная концентрация или активность ионов (ɑ_i)

 К сильным электролитам относятся вещества с ионными или сильно полярными связями: все хорошо растворимые соли, сильные кислоты (HCl, HBr, HI, HClO₄, H₂ SO₄ ,HNO₃) и сильные основания (LiOH, NaOH, KOH, RbOH, CsOH, Ba(OH)₂,Sr(OH)₂ и т.д. В растворе сильного электролита растворенное вещество находится в основном в виде ионов; недиссоциированные молекулы практически отсутствуют. Это приводит к тому, что силы межионного взаимодействия заметно проявляются даже при малой концентрации электролита. Втаких растворах ионы не вполне свободны, движение их стеснено взаимным ритяжениием друг к другу. Благодаря этому притяжению каждый ион как бы окружен шарообразным роем противоположно заряженных ионов, получившим название «ионной атмосферы». Следовательно, все свойства раствора электролита, зависящие от концентрации ионов, проявляются так, как если бы число ионов в растворе было меньше, чем это соответствует полной диссоциации электролита. Для оценки состояния ионов в растворе пользуются величиной, называемой активностью (ɑ_i). Под активностью иона понимают ту эффективную, условную концентрацию его, соответственно которой он действует при химических реакциях. Активность иона равна его молярной концентрации (С_м), умноженной на коэффициент активности (f_i) :

                                                        ɑ_i = f_i ∙ C_м.                                          (69)

2) Коэффициент активности (f_i)

Коэффициенты активности различных ионов различны, численное значение их зависит от состава и концентрации раствора, от заряда и природы иона и изменяется при изменении условии, в частности, при изменении концентрации раствора.  В концентрированных растворах коэффициент активности обычно меньше единицы, а с разбавлением раствора он приближается к единице. Значение, меньшее единицы, указывает на взаимодействие между ионами, приводящее к их взаимному связыванию. Если же коэффициент активности близок к единице, то это свидетельствует о слабом межионном взаимодействии. В разбавленных растворах (С_м ≤ 0,5 моль/л) природа иона слабо влияет на значение его коэффициента активности и зависит в основном только от заряда иона и ионной силы раствора (I). Вычислить коэффициент активности иона можно по формуле:

                                                        lg f_i = −0,5∙z²∙                                    (70)

 или обратиться к справочному материалу.

3) Ионная сила раствора (I)

Под ионной силой раствора понимают полусумму произведений концентраций (С_м) всех находящихся в растворе ионов на квадрат их заряда (z):

                                        I = 0,5(С₁∙ z²₁ +С₂∙ z²₂ +…+ С_n∙ z²_n).                     (71)

 Например, ионную силу раствора, содержащего 0,1 моль/л хлорида натрия и 0,1 моль/л хлорида бария можно рассчитать следующим образом; т.к. оба электролита являются сильными, то процессы их диссоциации можно записать:

а)NaCl → Na⁺ + Cl⁻ ;          б) ВaCl₂ → Вa²⁺ + 2Cl⁻ .

 Концентрация ионов хлора в электролите а) равна 0,1 моль/л, а в электролите б) равна 0,2 моль/л, общая концентрация хлорид ионов равна 0,3 моль/л; концентрация ионов натрия равна 0,1 моль/л и концентрация ионов бария составляет 0,1 моль/л. Таким образом: I= 0,5 (0,1∙1² + 0,1 ∙2² + 0,3∙(-1)²) = 0,4.

      5.4. Комплексные соединения

Комплексные соединения – это химические соединения надмолекулярного уровня организации вещества, в состав которых входят комплексные частицы, способные к существованию в растворах как отдельные кинетические единицы.

Комплексные соединения – это обширный класс неорганических и элементорганических соединений и широко распространены в природе. Они имеют важное теоретическое и (самое главное) прикладное значение: в аналитической химии (методы качественного и количественного анализа); в металлургии (методы получения химически чистых металлов из руд, редких металлов – Au, Pt, U и т.д.); в полупроводниковой промышленности (методы получения сверхчистых полупроводниковых материалов); получение катализаторов и красителей, лекарственных препаратов, в методах очистки природных и сточных вод, растворения накипи в парогенераторах и т. п. Комплексными соединениями являются два вещества, без которых невозможна жизнь на земле животных и растений – это гемоглобин крови (комплексообразователь Fe²⁺) и хлорофилл (комплексообразователь Mg²⁺).

    Состав и строение комплексных соединений

    Описание свойств и строения комплексных соединений представлено в координационной теории А. Вернера.

Основные положения координационной теории.

1. Большинство комплексных соединений имеют внутреннюю и внешнюю сферы. Записывая химические формулы комплексных соединений, внутреннюю сферу заключают в квадратные скобки, такая формула называется координационной. Например, в комплексных соединениях К[Al(OH)₄] и [Cu(NH₃)₄]Cl₂, внутренней сферой являются группы атомов (комплексы) — [Al(OH)₄]⁻ и [Cu(NH₃)₄]²⁺ (рис.15), а внешней сферой — ионы К⁺ и Сl^– соответственно.

2. Центральный атом, как правило, положительно поляризованный  называют комплексообразователем, например Cu²⁺ (рис.16). Обычно, в качестве комплексообразователей выступают атомы или ионы металлов с достаточным количеством свободных орбиталей в валентной структуре – это p-, d-, f- элементы: Cu²⁺, Pt²⁺, Pt⁴⁺, Ag⁺, Zn²⁺, Al³⁺и др. Но это может быть и атомы элементов, образующих неметаллы, например, азот или кремний ( ). Заряд комплексообразователя обычно положительный, но также может быть отрицательным или равным нулю и равен сумме зарядов всех остальных ионов. В приведенных выше примерах комплексообразователями являются ионы Al³⁺и Cu²⁺.

Cu2+

NH3

NH3

H3N

NH3

2+

Рис.15. Структура комплексного иона

3.Вокруг комплексообразователя в пространстве располагаются частицы – лиганды, которые связаны с комплексообразователем донорно-акцепторной или координационной ковалентной сигма связью. В качестве лигандов в комплексных соединениях могут выступать такие анионы, как F– , OH–, CN–, CNS–, NO²–, CO₃²–, C₂O₄²–и др., или нейтральные молекулы Н₂О, NН₃, СО, NО и др. В наших примерах это – ионы OH— и молекулы NH₃. Если комплексообразователем является положительно поляризованный атом (например, Al³+или Cu²+), то он является акцептором неподеленной электронной пары при образовании ковалентной связи, следовательно, в состав лиганд должны входить атомы, являющиеся донорами электронов, например, .

4. .Количество лигандов в различных комплексных соединениях лежит в пределах от 2 до 12. А само число лигандов (число сигма-связей) называется координационным числом (к.ч.) комплексообразователя. В рассматриваемых примерах к.ч. равно 4. Степень окисления комплексообразователя является основным фактором, влияющим на величину координационного числа. Как правило, координационное число равно удвоенной степени окисления комплексообразователя, но существуют исключения, например, Fe²⁺ и Fe³⁺, Ni²⁺,  Pt⁴⁺ имеют координационное число равное 6.

5. Заряд комплекса (внутренней сферы) определяется как сумма зарядов комплексообразователя и лигандов.

6. Внешнюю сферу образуют ионы, связанные с комплексом ионной или межмолекулярной связью и имеющие заряд, знак которого противоположен знаку заряда комплексообразователя. Числовое значение заряда внешней сферы совпадает с числовым значением заряда внутренней сферы. В формуле комплексного соединения они записываются за квадратными скобками. Внешняя сфера может и вовсе отсутствовать в случае, если внутренняя сфера нейтральна. В приведенных примерах, внешнюю сферу образуют 1 ион K⁺и 2 иона Cl^— соответственно. Внутренняя сфера комплекса в значительной степени сохраняет стабильность в растворе. Ионы внешней сферы в растворе легко отщепляются.

Классификация комплексных соединений

Основные (некоторые) классификации комплексных соединений.

1. По знаку заряда комплексной частицы:

а) катионный: данный комплекс образуется в том случае, если комплексообразователь заряжен положительно, а лигандами являются электронейтральные молекулы, например, [Al(H₂O)₆]³⁺, [Ag(NH₃)₂]⁺;

 б) анионный комплекс образуется, если лигандами являются анионы, например, [Fe(CN)₆]^3-, [AlF₆]^3-, [Cu(OH)₄]^2-;

в) нейтральный комплекс имеет заряд равный нулю, и такое комплексное соединение не имеет внешней сферы. Нейтральный комплекс может образоваться при одновременной координации  вокруг центрального положительно заряженного иона отрицательных ионов и молекул, заряд комплексообразователя и суммарный заряд лигандов по абсолютной величине становятся одинаковыми, например, [Pt(NH₃)₂Cl₂].

2. По типу лигандов.

Некоторые лиганды и их название приведены в табл.11

                                                                                                               Таблица 11

                         Название лиганда и комплекса

лиганд	Н2О	NH3	СО	ОН−	CN−	Cl—	NCS—	C2O42−	NO2—
Название лиганда	аква	аммин	карбонил	гидроксо	циано	хлоро	тиоционато	оксалато	Нитро
Название комплекса	гидрат	аммиакат	карбонил	гидроксокомплекс	ацидокомплексы, лигандами являются кислотные остатки

 

3. По химическим свойствам.

а) Комплексные соединения с внешнесферными катионами водорода  в водном растворе нацело подвергаются протолизу. Они являются сильными кислотами, например, гексафторосиликат водорода или гексахлороплатинат водорода: H₂[SiF₆]  → 2Н⁺ + [SiF₆]²⁻ ; H₂[PtCl₆] → 2Н⁺ + [PtCl₆]²⁻.

б) Если во внешней сфере комплексного соединения находятся гидроксид-ионы, то это соединение – сильное основание (диссоциация идет нацело, рН >> 7). Пример соединения этого типа – гидроксид тетраамминцинка(II):

 [Zn(NH₃)₄](OH)₂ → [Zn(NH₃)₄]²⁺ + 2 OH⁻.

в) Соли, в водных растворах диссоциирующие на комплексный ион и ионы внешней сферы:

 K₄[Fe(CN)₆] → 4 K⁺ + [Fe(CN)₆]⁴⁻; [Co(H₂O)₆]Cl₂ → [Co(H₂O)₆]²⁺+2 Cl⁻ .

г) Неэлектролиты, комплексные соединения, не имеющие внешней сферы. К неэлектролитам относят прежде всего внутрикомплексные соединения с органическими лигандами, карбонилы металлов [Fe(CО)₅] или [Ni(CО)₄] и некоторые другие, например, [Pt(NH₃)₂Cl₂].

Номенклатура комплексных соединений

     Чтобы записать формулу комплексного соединения, необходимо помнить, что, как для любого ионного соединения, вначале записывается формула катиона, а затем – формула аниона. Формулу комплекса записывают в квадратных скобках, где вначале записывают комплексообразователь, затем лиганды в круглых скобках и координационное число.

Для того чтобы составить название комплексного соединения необходимо соблюдать некоторые правила.

1. В названиях комплексных соединений, как и ионных солей, первым указывают анион, а затем – катион.

2. В названии комплекса сначала указывают лиганды, а после – комплексообразователь. Лиганды перечисляют в алфавитном порядке.

3. Нейтральные лиганды называются также, как молекулы, к анионным лигандам прибавляют окончание – о.

4. Если количество лигандов больше единицы, то их число указывают греческими приставками: 2-ди-, 3-три-, 4-тетра-, 5-пента-, 6-гекса-, 7-гепта-, 8-окта-, 9-нона-, 10-дека-.

5. Названия комплексных анионов оканчиваются суффиксом – ат.

После названия металла (комплексообразователя) в скобках указывают римскими цифрами его степень окисления

Примеры: К₃[FeF₆] – гексафтороферрат(III) калия;  [Pt(NH₃)₄Cl₂]Cl₂ − хлорид тетраамминдихлороплатины(IV).

    Устойчивость и диссоциация комплексных соединений в растворах

В растворах комплексных соединений могут происходить разнообразные сложные превращения, определяемые природой как самого комплексного соединения, так и растворителя. Внутренняя и внешняя сферы комплексного соединения сильно различаются по устойчивости.

а) Частицы внешней сферы связаны с комплексным ионом электростатическими силами (ионный тип связи) и легко отщепляются в водном растворе. Такая диссоциация называется первичной, она протекает нацело, по типу диссоциации сильных электролитов.

б) Во внутренней сфере химическая связь лиганд – комплексообразователь является ковалентной, возникшей по донорно–акцепторному механизму, с высокой энергией связи. Поэтому распад комплексной частицы является процессом обратимым (как диссоциация слабого электролита) и называется вторичной диссоциацией комплексного соединения. Растворимые комплексные соединения, не имеющие внешней сферы (нейтральные комплексы), ведут себя в растворах как слабые электролиты. Как любой обратимый процесс, диссоциация внутренней сферы комплексных электролитов и нейтральных комплексов является процессом равновесным. Количественной характеристикой равновесного процесса является константа равновесия (закон действующих масс), а т.к. в данном случае рассматривается диссоциация (распад) комплексной частицы, то константа равновесия называется константой нестойкости комплекса (К_Н).

Пример диссоциации в водном растворе комплексного соединения:

а) первичная диссоциация     K₃[Fe(CN)₆] → 3 K⁺ + [Fe(CN)₆]³⁻,

б) вторичная диссоциация [Fe(CN)₆]³⁻ ↔ Fe³⁺ + 6(CN)⁻,

выражение константы нестойкости: .                         (72)

Величина обратная константе нестойкости называется константой устойчивости комплекса (К_У), К_У = 1/ К_Н. Для большинства известных комплексных соединений константы нестойкости экспериментально определены (их значения указаны в справочниках физико-химических величин). Из выражения константы нестойкости можно сделать вывод: чем меньше значение константы нестойкости, тем более прочной (мало диссоциирующей) является комплексная частица.