Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

В 1957 г. Пекаром [37] впервые было отмечено, что пространственная дисперсия диэлектрической проницаемости вблизи экситонного резонанса может привести к появлению дополнительной распространяющейся световой (экситон-поляритонной) волны. Такая возможность связана с тем, что экситонное возбуждение в среде может перемещаться (например от одной молекулы к другой) и его энергия зависит от волнового вектора к. Рассмотрим выражение (28) для поперечной диэлектрической проницаемости, определяемой откликом, соответствующим изолированному электрическому дипольно-разрешенному экситонному переходу с частотой ω _L . Матричные элементы (25) "отбирают" только экситонные состояния \ n > с импульсом (квазиимпульсом) nк, а значит, энергии ω_п - те энергии, которые соответствуют этому импульсу. В приближении эффективной массы дисперсия энергииэкситона имеет вид

 

 

Соответственно, поперечная диэлектрическая функция выражается как

 

 

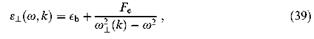
что для неподвижных экситонов (М_ехс = оо) совпадает с уравнением (28). Конечно, сила осциллятора F_e тоже может зависеть от к, но мы ограничимся более сильным эффектом, связанным с резонансным знаменателем в уравнении (39). Кстати, заметим, что пространственную дисперсию, например, такого вида, как в уравнении (39), нельзя учесть с помощью ε(ω)-µ(ω)-описания. Из уравнений (16) и (39) легко найти дисперсию поперечных поляритонов, примеры которой приведены на рис. 4.

Рисунок 4 показывает, что в некоторой области частот ω для каждой частоты действительно могут найтись два значения волнового вектора к, соответствующие двум поперечным поляритонным ветвям с одной и той же поляризацией. Та из них, которая имеет больший волновой вектор (обозначенный как к₂), и есть предсказанная Пекаром дополнительная волна.

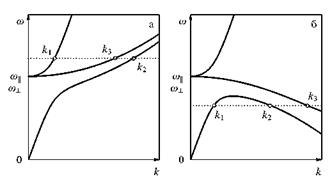Рис. 4. Дисперсия двух поперечных поляритонных ветвей и продольной волны в системе с дисперсией экситона (38): (а) эффективная масса экситона положительна, М_{е xc} > 0; (б) отрицательная эффективная масса, М_{е x с} < 0.

 

Наиболее убедительные эксперименты были проведены в полупроводниках вблизи резонанса, отвечающего экситону Ваннье-Мотта (см. обсуждение и ссылки на литературу в [7]). Принципиальное значение для знака групповой скорости имеет знак эффективной массы экситона. Обычно эффективная масса экситона Ваннье-Мотта положительна: М_ехс = т_е + m_h >0, где т_е и m_h -соответственно эффективные массы электронов и дырок. Такая ситуация изображена на рис. 4а. Очевидно, что добавочная волна в этом случае имеет положительную групповую скорость.

Однако в органических кристаллах радиус экситонов Френкеля обычно мал. В такой ситуации резонансное взаимодействие между молекулами сильно зависит от их ориентации, что приводит к тому, что эффективная масса экситона, вообще говоря, может быть отрицательной или иметь разные знаки для разных направлений. Случай отрицательной эффективной массы показан на рис. 46. Ясно видно, что для некоторого интервала частот ω добавочная поперечная поляритонная волна (волна с волновым вектором к₂) имеет отрицательную групповую скорость. Именно эта поперечная волна будет испытывать отрицательное преломление.

На рисунке 4 также показана дисперсия продольных волн, определяемая уравнением (17). Для определенности мы положили ε(ω, k )= ε_L {ω, k ). Волновой вектор продольной волны обозначен через к_г. Если М_ехс < 0, то продольные волны в этом приближении также имеют отрицательную групповую скорость. В общем случае все три волны (две поперечных и одна продольная) можно возбудить в среде с помощью падающей волны, имеющей соответствующую частоту. Для того чтобы решить задачу об отражении и прохождении волн в этом случае, следует ввести так называемые дополнительные граничные условия (ДГУ), поскольку, очевидно, обычно используемых граничных условий Максвелла будет недостаточно для нахождения амплитуд всех возбужденных волн. Явный вид ДГУ зависит от микроскопической природы экситонов. Для молекулярных кристаллов этот вопрос подробно обсуждается в [7].

В недавней работе [38] проведено численное моделирование отражения и прохождения света через плоскую пластину, сделанную из материала, в котором экситоны имеют отрицательную эффективную массу, М_ехс < О (рис. 46). Эти расчеты убедительно показали, что благодаря отрицательному преломлению волн с отрицательной групповой скоростью такая пластина действительно приводит к фокусировке излучения. Результаты численного моделирования [38] также указывают на то, что для экспериментальной реализации такой системы необходим кристалл с большой силой осциллятора экситонного перехода и достаточно слабой диссипацией добавочных поляритонов при частотах ниже частоты экситонного резонанса.