Макроскопические уравнения Максвелла составляют основу электродинамики сплошных сред [6]. Они выводятся усреднением "микроскопических" электромагнитных полей, зарядов и плотностей тока и должны дополняться так называемыми материальными уравнениями - связями между усредненными полями. Материальные уравнения определяются откликом среды на электромагнитное поле. Следуя Ландау и Лифшицу [6] (см. также [7, 23]), представляется более правильным и удобным использовать подход, основанный на учете пространственной дисперсии, в котором рассматриваются только три макроскопических поля: Е, D, В, а четвертое поле, Н, полагается равным В. В рамках этого подхода результат усреднения всех микроскопических токов включается в определение поля D. Макроскопические уравнения Максвелла для монохроматических плоских волн принимают вид

а связь между компонентами полей D и Е (материальное уравнение) выражается как

В уравнении (9) обобщенный диэлектрический тензор ε(ω,к) зависит от волнового вектора к. Это означает, что учтена пространственная дисперсия, т.е. тот факт, что индукция электрического поля D в данной точке пространства зависит не только от электрического поля Е в этой точке (что соответствовало бы локальному отклику), но также и от электрического поля в некоторой ее окрестности (нелокальный отклик). По существу, тензор ε(ω,к) описывает и электрический, и магнитный отклики среды (второй из них - при естественном учете пространственных производных поля Е). Пространственная дисперсия появляется как добавление к более привычной временной, или частотной, дисперсии, выражающейся в зависимости диэлектрического тензора от ω. Обычно эффекты, связанные с пространственной дисперсией, являются гораздо более слабыми, чем эффекты, связанные с временной дисперсией, но первые могут приводить к качественно новым явлениям, таким, например, как гиротропия или возникновение добавочных электромагнитных волн. Рассмотрение пространственной дисперсии упрощается, если соответствующий параметр ка ~ а/λ мал (здесь а - характерный микроскопический размер или длина свободного пробега заряженных частиц). Малость параметра ка позволяет во многих случаях учитывать только первые члены (линейные и/или квадратичные) в разложении тензора ε(ω,к) по степеням компонент волнового вектора к [6, 7]:

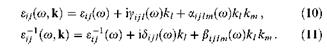
Разные тензоры, стоящие в разложениях (10) и (11), отражают свойства симметрии рассматриваемой системы и удовлетворяют принципу симметрии кинетических коэффициентов Онсагера. В частности, в системе, обладающей центром инверсии, вторые члены разложения (т.е. пропорциональные первой степени к,) исчезают.

Поскольку из уравнений Максвелла (8) сразу следует, что

уравнения (12) и (9), взятые вместе, определяют уравнения дисперсии ω(к) электромагнитных волн в среде.

Усредненную по времени плотность энергии и вектор Пойнтинга в обсуждаемом (E,D, В)-подходе можно найти, рассматривая волновые пакеты [6, 7]. Указанные величины задаются соответственно выражениями

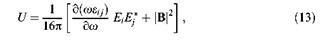
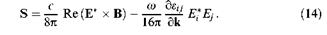
Соотношения (13) и (14) в отсутствие диссипации удовлетворяют закону сохранения энергии. Наличие дополнительного (второго) слагаемого в уравнении (14) [24,25] -результат учета пространственной дисперсии. Этот член играет определяющую роль в появлении волн с отрицательной групповой скоростью.

В дальнейшем мы приведем краткое сравнительное обсуждение (см. раздел 3.2) обоих подходов: (E,D,B)-подхода, учитывающего пространственную дисперсию, и так называемого "симметричного" подхода, основанного на рассмотрении всех четырех полей, Е, D, В, Н. Тем не менее мы отсылаем читателя к книге [26], обзорам [27-29] и недавней статье [8], в которых можно найти обсуждение различных точек зрения, другие аргументы и подробности.