Рассмотрим простую систему массового обслуживания: число каналов равно
единице, время ожидания неограниченно, время между заявками и время
обслуживания заявок являются случайными величинами с показательным
законом распределения (среднее значение времени обслуживания равно to ,
среднее время между заявками - tz ) (рис.2.2).
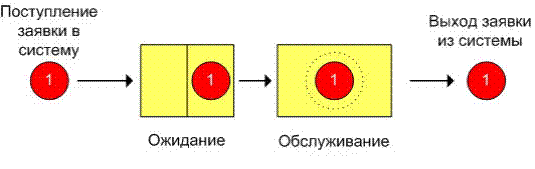
Рис. 2.2 – Одноканальная система массового обслуживания
Рассмотрим процесс поступления десяти заявок, если tz =0,5 ч., to =1 ч.
В [6] использован следующий способ моделирования такой системы
(рис.2.3). Величины времени обслуживания и между заявками рассчитываются
согласно способу моделирования случайной величины с показательным законом
распределения
D7=-$F$3*LN(СЛЧИС())
E7=-$F$2*LN(СЛЧИС()).
В последнем столбце рассчитывается величина Wn + Xn −Yn
F7=C7+D7-E7.
Если ее значение является отрицательным, то это означает, что следующая
заявка поступит после того, как будет обслужена текущая и потому время ее
ожидания будет равно нулю, а в противном случае, время ожидания составит
Wn + Xn −Yn
С8=ЕСЛИ(F7>0;F7;0).
.
Изменим исходные данные ( tz =1 ч., to =0,5 ч.). Из рис. 2.4 можно увидеть, что
в этом случае уменьшится время ожидания обслуживания.

Рис.2.3 – Результаты моделирования одноканальной СМО при tz =0,5 ч., to =1 ч.

Рис. 2.4 – Результаты моделирования одноканальной СМО при tz =1 ч., to =0,5 ч.
Теперь выполним моделирование, учитывая начальное время tn . Пусть tz =8
мин., to =7 мин.; tn =9 ч. Рассмотрим процесс поступления семи заявок (рис.2.5).
Определение времени между заявками и времени обслуживания (мин.) остается
без изменения.
Для того чтобы перевести эти значения в используемый формат времени
необходимо осуществить следующие операции
F8=E8/1440
D8=D7+C8/1440.
Т.е. время поступления очередной заявки равно сумме времени прибытия
предыдущей и случайной величины, распределенной по показательному закону.
Время начала обслуживания первой поступившей заявки равно времени ее
поступлению
G8=D8.
Начиная со второй заявки, эта величина будет определяться как
максимальное значение из момента окончания обслуживания предыдущей заявки
и времени поступления текущей
G9=ЕСЛИ(D9>=H8;D9;H8).
Время окончания обслуживания рассчитывается по формуле
H8=G8+F8.
Период ожидания равен разности времени начала обслуживания и времени
поступления
I8=G8-D8.
Также встречаются системы, в которых новая заявка может поступить только
после того, как была обслужена предыдущая. В качестве примера, можно назвать
систему, которая периодически может выходить из строя и требовать ремонта (ее
отказы в данном случае рассматриваются как заявки): время между ее отказами и
время обслуживания распределено по показательному закону. Очевидно, что не
может произойти выход из строя системы прежде, чем будет выполнен ремонт
предыдущего отказа. Такие заявки будем называть не перекрывающимися.
Для того чтобы выполнить моделирование данной СМО необходимо
изменить только расчет времени прибытия заявки, которое будет равно сумме
момента окончания обслуживания предыдущей заявки и случайной величины,
распределенной по показательному закону
D9=H8+C9/1440.
Результаты моделирования представлены на рис.2.6 ( tz =5 мин., to =6 мин.).
Можно заметить, что в Диаграмме заявок теперь отсутствуют периоды ожидания
обслуживания.
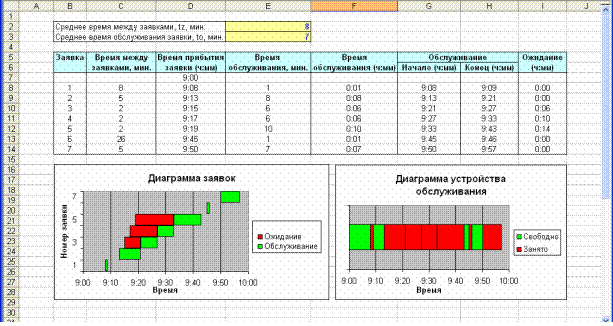
Рис. 2.5 – Моделирование одноканальной СМО с учетом начального времени
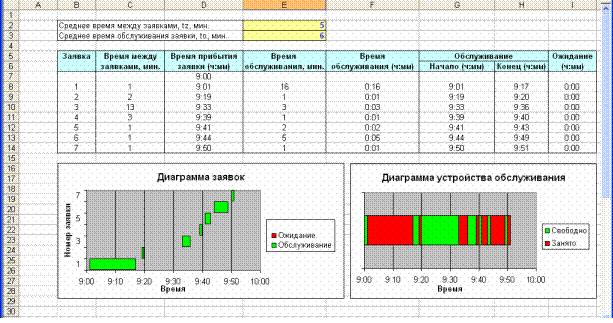
Рис. 2.6 – Моделирование одноканальной СМО с не перекрывающимися
заявками
Задание
1. Выполните имитацию работы банка, осуществляющего прием вкладов.
Размер депозита является случайной величиной с нормальным законом
распределения (среднее значение -MD ; среднее квадратическое
отклонение - SD ). Время между приходом двух вкладчиков – случайная
величина с показательным законом распределения (среднее значение - tz ),
а время обслуживания равномерно распределено на интервале [ a ; b ].
Пусть исходные значения равны величинам: MD =30000 руб.; SD =10000
руб.; tz =1 час; a =20 мин.; b =30 мин.; tn =9 ч., число заявок равно 5.
Определите время прихода последнего клиента, среднее время
пребывания клиента в системе. Какой общий размер вкладов будет
осуществлен а) после прихода пяти клиентов; б) к моменту времени 12:00
ч.?

Рис.2.7 – Система массового обслуживания ≪Банк≫
2. Проведите 10 экспериментов и рассчитайте величины:
• среднее время ожидания;
• среднее число обслуженных заявок за период с 9:00 до 15:00 ч.
3. Предположите, что tn =0 и выполните имитацию описанным на рис. 2.3
способом.
4. Пусть банковская автоматизированная система может выходить из строя,
что приводит к необходимости вызова специалистов, устраняющих
неполадку. Выполните имитацию периодов нормальной работы системы и
ее ремонта, если данные величины являются случайными с показательным
законом распределения, а tz =30 дней, to =3 ч. Рассмотрите процесс
поступления 5 заявок (отказов).
Практическая работа № 32
Тема: Моделирование системы управления запасами.
Цель урока:
· Освоить 3Д-технологии построения ломаного разреза;
· Развивать умения применять формулируемые знания в новых ситуациях;
· Воспитывать самоанализ в новых ситуациях.
Оборудование:
· Компьютеры;
· Программа AutoCAD;
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
· Какой сложный разрез называется ломаным;
· Особенности выполнения ломаного разреза предусмотренные ГОСТ 2.305-68;
· Порядок анализа формы детали.
Студент должен уметь:
· Выполнять построение ломаного разреза;
· Анализировать форму детали;
· Использовать команды для замыкания и выдавливания контура;
· Вычерчивать контур вращения;
· Объединять элементы основания;
· Применять команды вычитания тела.
Вопросы для повторения
1. Что должен содержать чертёж, построенный по 3Д-технологии;
2. Какой сложный разрез называется ломаным?
3. Какой порядок выполнения настроек используется для построения чертежей по 3Д-технологии?
4. Как построить контур выдавливания?
5. Какой порядок замыкания контура?
Ход работы:
Задачи управления запасами составляют один из наиболее
многочисленных классов экономических задач исследования операций.
Правильное и своевременное определение оптимальной стратегии управления
запасами, а также нормативного уровня запасов позволяет высвободить
значительные оборотные средства, замороженные в виде запасов, что, в
конечном счете, повышает эффективность используемых ресурсов.
На рис. 4.1 приведены основные элементы системы управления запасами,
где пунктирными линиями показано перемещение информационных потоков, а
сплошными – передвижение ресурсов. При этом запасом может быть не только
некоторый товар на складе (полуфабрикаты, готовые изделия, материалы), но и
информационные, трудовые, финансовые водные и другие виды ресурсов. В
качестве поставщиков могут выступать как контрагенты организации, так и
различные объекты, находящиеся внутри самой системы (например, готовая
продукция поступает на склад из производственного цеха, а затем отгружается
покупателям).
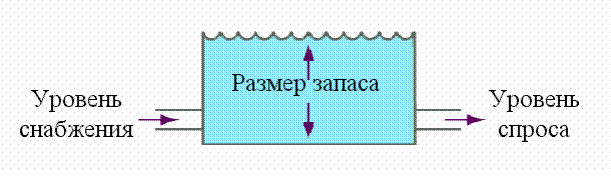

Рис. 4.1 - Движение товарного запаса на складе
Необходимость иметь запасы обуславливается наличием хотя бы одного из
следующих факторов:
1. колебание спроса на товары;
2. колебание сроков поставки товаров предприятия;
3. определенные условия, требующие закупки продукции партиями.
Существует обширная классификация систем управления запасами.
Рассмотрим характеристики ее элементов [14].
Спрос. Спрос на запасаемый продукт может быть детерминированным (в
простейшем случае — постоянным во времени) или случайным. Случайность
спроса описывается либо случайным моментом спроса, либо случайным объемом
спроса в детерминированные или случайные моменты времени.
Пополнение склада. Пополнение склада может осуществляться либо
периодически через определенные интервалы времени, либо по мере исчерпания
запасов, т. е. снижения их до некоторого уровня. Причем доставка может
осуществляться как всего товара сразу, так и в течение определенного периода
времени.
Объем заказа. При периодическом пополнении и случайном исчерпании
запасов объем заказа может зависеть от того состояния, которое наблюдается в
момент подачи заказа (например, может быть равен спросу). Заказ обычно
подается на одну и ту же величину при достижении запасом заданного уровня —
так называемой точки заказа. Объем заказа может быть случайной величиной
(например, это может быть связано с ненадежными поставщиками либо доставкой
сельскохозяйственной продукции, когда величина урожая неизвестна) или
детерминированной.
Время доставки. В идеализированных моделях управления запасами
предполагается, что заказанное пополнение доставляется на склад мгновенно. В
других моделях рассматривается задержка поставок на фиксированный или
случайный интервал времени.
Стоимость поставки. Как правило, предполагается, что стоимость каждой
поставки слагается из двух компонент — разовых затрат, не зависящих от объема
заказываемой партии, и затрат, зависящих (чаще всего — линейно) от объема
партии.
Издержки хранения. В большинстве моделей управления запасами
считают объем склада практически неограниченным, а в качестве
контролирующей величины служит объем хранимых запасов. При этом полагают,
что за хранение каждой единицы запаса в единицу времени взимается
определенная плата.
Штраф за дефицит. Отсутствие запаса в нужный момент приводит к
убыткам, связанным с простоем оборудования, неритмичностью производства и т.
п. Эти убытки в дальнейшем будем называть штрафом за дефицит. При
возникновении дефицита величина неудовлетворенного спроса может
учитываться в последующие периоды (считается, что покупатели ждут, пока
поступит товар на склад), в противном случае предполагается, что клиенты
приняли решение о покупке товара у других фирм.
Номенклатура запаса. В простейших случаях предполагается, что на
складе хранится запас однотипных изделий или однородного продукта. В более
сложных случаях рассматривается многономенклатурный запас.
Структура складской системы. Наиболее полно разработаны
математические модели одиночного склада. Однако на практике встречаются и
более сложные структуры: иерархические системы складов с различными
периодами пополнения и временем доставки заказов, с возможностью обмена
запасами между складами одного уровня иерархии и т. п. Системы управления
запасами могут быть частью более обширной логистической системы (рис. 4.2).__
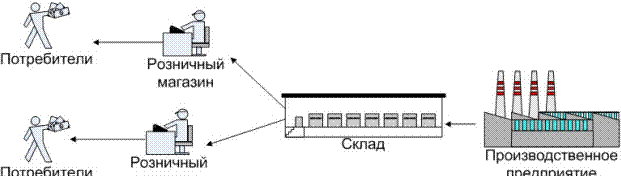
Рис. 4.2 – Пример логистической цепи
В качестве показателя эффективности принятой стратегии управления
запасами выступает функция затрат (издержек), представляющая суммарные
затраты на хранение и поставку запасаемого продукта (в том числе потери от
порчи продукта при хранении и его морального старения, потери прибыли от
омертвления капитала и т. п.) и затраты на штрафы. В этом случае управление
запасами состоит в отыскании такой стратегии пополнения и расхода запасами,
при котором функция затрат принимает минимальное значение. Однако,
встречаются и другие показатели, такие как уровень обслуживания покупателей,
показатель выполнения плана реализации, оценка работы поставщиков
(своевременность доставки), сокращение излишних запасов, рентабельность
активов и т.д.
В теории управления запасами приводится аналитическое решение
некоторых задач. Необходимость использования метода имитационного
моделирования обусловлена наличием стохастических факторов (случайный
спрос, время доставки и т.д.) в системах управления запасами. Так, по мнению
Ingals [15], если ключевой особенностью системы является колебания входных
значений, то имитационное моделирование является лучшим инструментом ее
исследования. Также он отмечал, что данный метод прекрасно подходит, если
рассматривается система, в которой имеются сложные связи между элементами и
действует набор специфических правил, например, существует особая схема
распределения товара между покупателями согласно их приоритету.
Кроме того, этот метод подходит для выявления так называемых ≪узких
мест≫ предприятия, которые ограничивают продвижение в системе
материальных, информационных и финансовых потоков.
Среди программных систем, предназначенных для имитации управления
запасами и цепей поставок можно назвать системы SIMLOX, SISCO, игры The
Beer Game, Distribution Game (рис.4.3), Global Supply Chain Game и т.д. Решение
задач управления запасами с помощью электронных таблиц приведено в работах
[1,7]. В [1] описано моделирование системы управления запасами с
периодической и пороговой стратегиями подачи заявок с учетом и без учета
отложенного спроса (модели названы ≪Склад≫ и ≪Магазин-Склад≫). На сайте [7]
представлена однопериодная модель со случайным спросом.
По данным компании XJ Technologies (производитель среды имитационного
моделирования Anylogic) наибольшим спросом сегодня пользуются именно
имитационные модели, реализованные для области логистики [16].__
Рассмотрим однопериодную модель управления запасами. Предположим,
что необходимо определить размер заказываемой партии Part на какой-то
будущий промежуток времени, если известно, что спрос D – случайная величина
с нормальным законом распределения (среднее значение равно MC , среднее
квадратическое отклонение - SC ). В том случае, если спрос будет меньше той
партии, которая была заказана, то издержки составят величину
С = Ch ⋅ (Part − D) ,
где Ch - стоимость хранения единицы товара.
В случае если заказанной партии окажется недостаточно для
удовлетворения спроса, то затраты будут включать издержки дефицита
С = Cd ⋅ (D − Part) ,
где Cd - штраф за дефицит единицы товара.
В работе [3] в качестве примера такой системы рассматривается заказ хот-
догов для игры в бейсбол. В процессе имитации необходимо оценить общие
издержки, соответствующие выбранному объему заказа. Моделирование системы
в течение 15 реализаций представлено на рис. 4.4. При этом были использованы
следующие исходные данные: Ch =60 руб.; Cd =160 руб.; Part =50 шт.; MC =40 шт.;
SC =10 шт. Размер спроса генерируется согласно способу моделирования
случайной величины с нормальным законом распределения (полученное
значение округляется)
D11=ЦЕЛОЕ($D$6+$D$7*((СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧ
ИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС())-6))
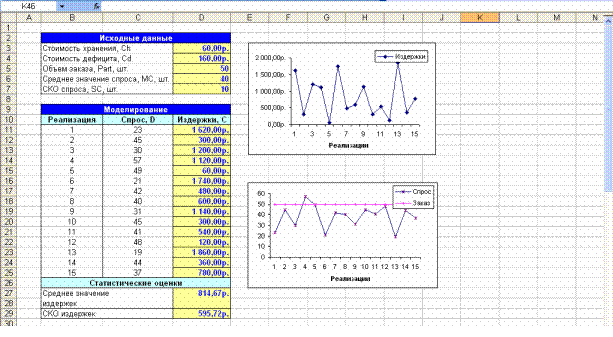
Рис.4.4 - Моделирование однопериодной системы управления запасами со
случайным спросом
Издержки рассчитываются согласно описанным выше формулам
D11=ЕСЛИ(C11<$D$5;$D$3*($D$5-C11);$D$4*(C11-$D$5)).
На рис. 4.5 приведены результаты экспериментов, полученные с помощью
≪Таблицы подстановки≫ (см. Приложение 5), при изменении величины
заказанного объема партии (примем значения 30,40,50,60,70,80, 90 шт.). Из
рисунка можно увидеть, что минимальное значение затрат достигается в точке,
когда объем партии равен 50 шт.
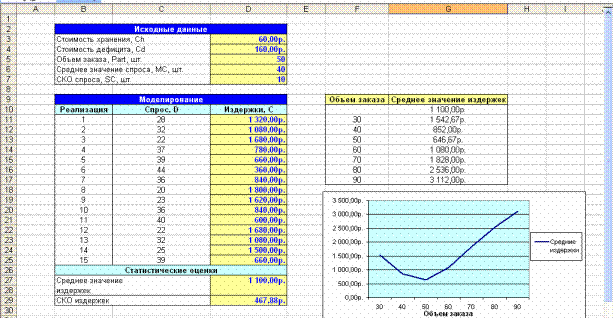
Рис. 4.5 – Исследование влияния объема заказанной партии на средние
издержки
Задачи
1. Реализуйте однопериодную модель и проанализируйте полученные
результаты. Какая ситуация возникает чаще: нехватка товара или его
избыток? Изменяя значение заказанного объема партии, найдите такую его
величину, при которой издержки будут наименьшими.
2. Рассчитайте вероятность дефицита товара (отношение реализаций, в
которых наблюдалась нехватка запаса, к общему количеству случайных
реализаций).
Дата: 2019-12-10, просмотров: 1234.