Рассмотрим механизм моделирования простого события. Пусть имеется

событие A, вероятность наступления которого равна P A. Выберем с помощью

датчика случайных чисел, равномерно распределенных в интервале (0,1)

некоторое число z . Известно, что вероятность попадания в интервал (0,P A)

случайной величины z равна величине P A. Поэтому если при розыгрыше число

z попало в этот интервал, то следует считать, что событие A произошло.

Противоположное событие (не A) произойдет с вероятностью (1 –P A) в том

случае, если z ≥ P A.

Процедура моделирования простого события в имитационной модели

описывается алгоритмом, схема которого показана на рис. 1 [23]. Оператор 1

обращается к датчику случайных чисел, генерирующему случайную величину z .

Оператор 2 проверяет условие z < P A. Если оно выполняется, считается, что

произошло событие A. В противном случае считается, что произошло противопо-

ложное событие (не A).

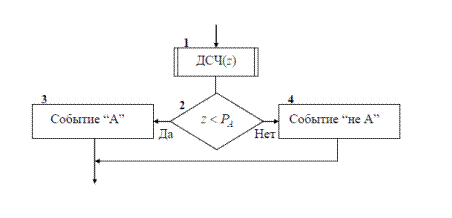
Рис.1 – Моделирование простого события

В Excel данную операцию можно реализовать с помощью функции ЕСЛИ.

Пусть в ячейке А1 указана вероятность P A события, тогда моделирование его

наступления будет выглядеть следующим образом

ЕСЛИ(СЛЧИС()<A1;”Событие А”;”Событие не А”).

Моделирование полной группы несовместных событий

Пусть имеется полная группа несовместных событий A1, A2,..., A k с

вероятностями P1,P2,...,P k . При этом выполняется условие

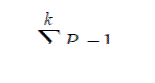
Процедура моделирования полной группы несовместных событий

описывается алгоритмом, схема которого показана на рис. 2. Здесь L i -

кумулятивная вероятность

L i = P1 + P2 + ...+ P i .

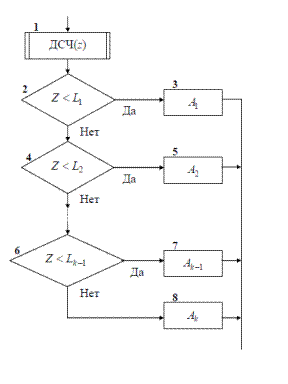
Рис. 2 – Алгоритм моделирования полной группы несовместных событий

Оператор 1 обращается к датчику случайных чисел с равномерным

распределением в интервале (0,1). Условный оператор 1 проверяет условие

попадания случайной величины z в интервал (0, L1). Если это условие

выполняется, то считается, что произошло событие A1. Если условие в операторе

2 не выполняется, то алгоритм осуществляет проверку условий попадания

случайной величины в другие интервалы. Одно из событий A1, A2,..., A k обя-

зательно произойдет.

Рассмотрим выполнение данных операций в Excel. Запишем в ячейки С2:С4

значения вероятностей P1,P2,P3 событий A1, A2, A3 (рис.3). В ячейке С5

смоделируем случайную величину, распределенную равномерно на интервале

(0,1). Тогда определение произошедшего события будет выглядеть следующим

образом

С6=ЕСЛИ(C5<C2;"A1";ЕСЛИ(C5<(C2+C3);"A2";"A3")).

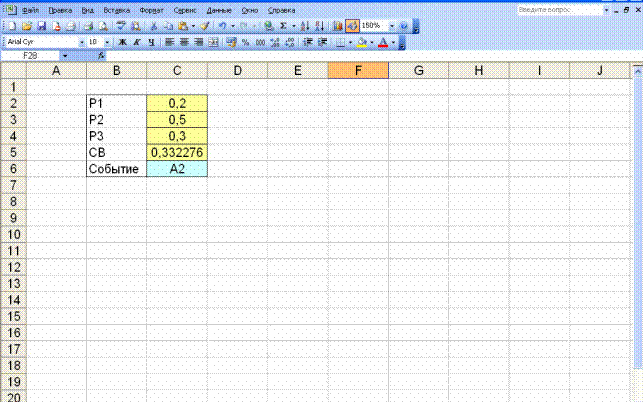
Рис. 3 – Моделирование полной группы несовместных событий