Согласно критерию оптимальности, решение выше не оптимально, так как в оценочной таблице присутствует отрицательное значение.
Дабы не загромождать решение множеством таблиц, оценочная матрица в нашем решении будет "вписана" в правую таблицу.
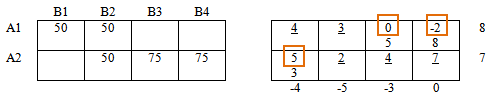
Подчеркнутые значения - базисные ячейки, как сказано выше, значения оценочной матрицы в базисных ячейках равны нулю, нули писать не будем. Выделенные значения - значения оценочной матрицы в свободных ячейках, среди них ищем отрицательные значения.
Для перехода к следующему опорному решению выполним следующее (построим цикл пересчета):
- найдем среди отрицательных значений оценочной матрицы максимальный по модулю (или по другому, минимальный среди отрицательных)
- в соответствующей ячейке левой таблицы ставим знак " + "
В нашем примере наименьшее отрицательное значение -2.
Знак " + " ставим в ячейке 1-й строки, 4-го столбца левой таблицы - ячейка соответствующая значению (-2).
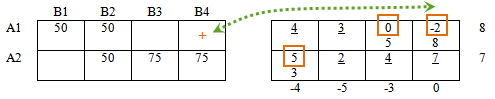
Необходимо расставить чередующиеся значения "+ " и " — " в левой таблице так, чтобы получился замкнутый цикл и выполнялись правила:
- остальные знаки цикла (все кроме уже поставленного первого " + ") ставим только в заполненных (базисных) ячейках таблицы,
- если в строке есть "плюс" ("минус"), то в этой строке должен быть и "минус" ("плюс"),
- если в столбце есть " плюс" ("минус"), то в этом столбце должен быть и "минус" ("плюс").
Применим к нашей таблице:
В столбце В4 есть "плюс", следовательно в этом столбце должен быть и "минус".
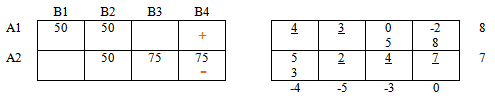
Аналогично, в строке А2 есть "минус", следовательно должен быть и "плюс".
Если мы поставим этот "плюс" в столбце В3, то цепочка порвется, так как в этом же столбце невозможно поставить "минус" — нет заполненной ячейки.
Ставим " + " в столбце В2 и продолжаем чередовать знаки.
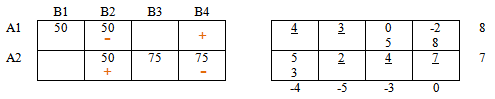
Получили замкнутый цикл чередующихся знаков. Цикл пересчета найден!
Далее обратимся к ячейкам, содержащим "минусы". Среди значений этих ячеек найдем минимальное: Δ = мин {50;75} = 50
К "плюсам" прибавим найденное Δ = 50, в ячейках с "минусами" — вычтем Δ = 50.
Ячейка, в которой находилось значение Δ = 50 останется пустой. В ячейке в которой мы поставили первый плюс появится значение, равное Δ = 50.
Общее количество заполненных (базисных) ячеек при пересчете не должно изменится!
Получили следующий опорный план:
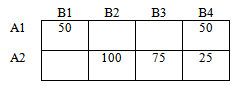
Вычислим стоимость перевозки на первом шаге.
Для этого найдем сумму произведений значений опорного плана и матрицы стоимостей.
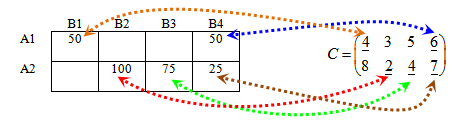
S1 = 50 · 4 + 100 · 2 + 75 · 4 + 25 · 7 + 50 · 6 = 1275
На первом шаге решения транспортной задачи получили опорный план:
Общая стоимость перевозки S1 = 1275
Метод потенциалов — шаг 2
Алгоритм проверки плана на оптимальность и построение цикла пересчета очень подробно расписан в шаге 1.
Далее решение задачи будем излагать менее детально.
Для полученного опорного решения строим вспомогательную — правую таблицу и заполняем значениями из матрицы стоимостей базисные ячейки.
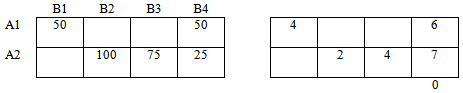
Вычисляем потенциалы строк и столбцов:
По правилу суммирования соответствующих потенциалов, заполняем свободные ячейки.
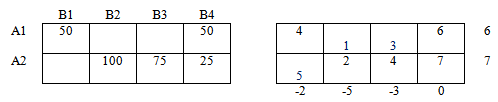
Вычисляем оценочные значения в свободных ячейках.
Для этого из значений матрицы стоимостей вычитаем найденные значения соответствующих свободных ячеек.
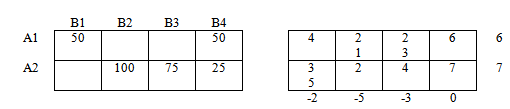
Среди оценочных значений нет отрицательных, следовательно план перевозки оптимален.
Получили оптимальный план. Итоговая стоимость перевозки S1 = 1275
ЗАДАЧА № 1 Три склада (A1-A3) поставляют в три магазина (B1-B3) розничной сети некоторый товар. Запасы данного товара на складах (шт.), потребности в нем магазинов (шт.)и тарифы на перевозку (в расчете на 1 шт.) показаны в транспортной таблице ниже. Найдите оптимальный план грузоперевозок, обеспечивающий удовлетворение потребностей магазинов в товаре с минимальными издержками на его транспортировку.
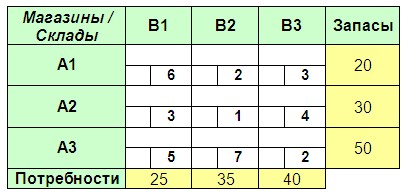
ОТВЕТСкрыть Оптимальный план перевозок будет следующим – A1-B2 = 20 шт., A2-B1 = 15 шт., A2-B2 = 15 шт., A3-B1 = 10 шт., A3-B3 = 40 шт. Затраты на грузоперевозки = 230 ден. ед.
ЗАДАЧА № 2 Два поставщика (A1-A2) обеспечивают четыре завода (B1-B4) необходимым для производства продукции сырьем. Запасы сырья на складах поставщиков (т.), потребности в нем заводов (т.) и тарифы на перевозку (в расчете на 1 т.) приведены в транспортной таблице ниже. Найдите оптимальный план грузоперевозок, обеспечивающий удовлетворение потребностей заводов в сырье с минимальными издержками на его транспортировку.
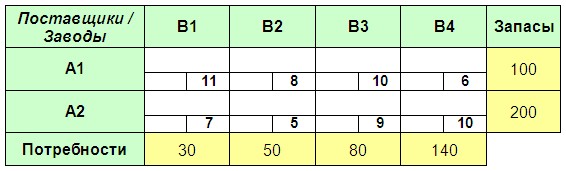
ОТВЕТСкрыть Оптимальный план перевозок будет следующим – A1-B4 = 100 т., A2-B1 = 30 т., A2-B2 = 50 т., A2-B3 = 80 т., A2-B4 = 40 т. Затраты на грузоперевозки = 2180 ден. ед.
ЗАДАЧА № 3 (с фиктивным потребителем) Три склада (A1-A3) поставляют в три магазина (B1-B3) розничной сети некоторый товар. Запасы данного товара на складах (шт.), потребности в нем магазинов (шт.)и тарифы на перевозку (в расчете на 1 шт.) приведены в транспортной таблице ниже. Найдите оптимальный план грузоперевозок, обеспечивающий удовлетворение потребностей магазинов в товаре с минимальными затратами на его транспортировку.
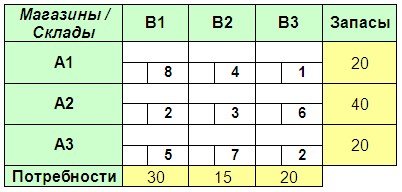
ОТВЕТ Скрыть Оптимальный план перевозок будет следующим – A1-B2 = 5 шт., A1-B3 = 15 шт., A2-B1 = 30 шт., A2-B2 = 10 шт., A3-B3 = 5 шт., A3-B4 = 15 шт. Затраты на грузоперевозки = 135 ден. ед.
Открытая транспортная задача - пример 1:
Решить транспортную задачу с исходными данными:
Общие потребности (спрос) = 40 + 180 + 80 + 60 = 360
Общие запасы (предложение) = 120 + 100 = 220
Видим, что спрос превышает над предложением.
Следовательно добавляем фиктивного поставщика А3 с объем запасов 360 - 220 = 140.
Получили закрытую транспортную задачу: спрос = предложению.
Построим первоначальный план методом северо-западного угла:
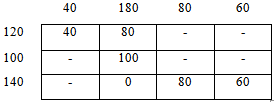
Шаг 1:
Проверим первоначальный план на оптимальность:
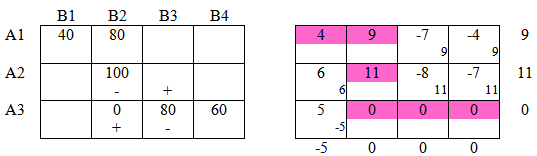
Подробно о том, как были заполнены таблицы можно посмотреть тут: Как решить транспортную задачу?
Среди оценочных значений правой таблице есть отрицательные, следовательно план не оптимален.
Построили замкнутую цепочку знаков " + " и " — ".
Среди ячеек, помеченных " — " выберем ячейку с минимальным значением:
К = min{80;100}=80
Это значение 80 перенесем в пустую ячейку, помеченную " + ", далее, к значениям в ячейках с " + " прибавим К, из значений в ячейках с " — " вычтем К.
Определим стоимость перевозки на первом шаге:
S1 = 40 · 4 + 80 · 9 + 100 · 11 + 0 · 0 + 80 · 0 + 60 · 0 = 1980
Шаг 2:
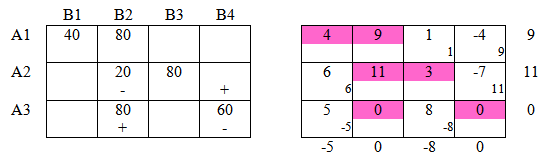
К = min{20;60}=20
Среди оценочных значений правой таблице есть отрицательные, следовательно план не оптимален.
В ячейках с " + " прибавим данное значение, в ячейках с " — " вычтем.
Общая стоимость перевозки на данном шаге:
S2 = 40 · 4 + 80 · 9 + 20 · 11 + 80 · 3 + 80 · 0 + 60 · 0 = 1340 < S1
Видим, что стоимость перевозки на текущем шаге меньше чем на предыдущем.
Шаг 3:
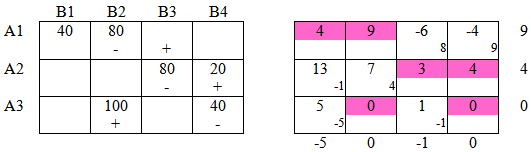
К = min{80;40}=40
Среди оценочных значений правой таблице есть отрицательные, следовательно план не оптимален.
Общая стоимость перевозки на данном шаге:
S3 = 40 · 4 + 80 · 9 + 80 · 3 + 20 · 4 + 100 · 0 + 40 · 0 = 1200 < S2
Видим, что стоимость перевозки на текущем шаге меньше чем на предыдущем.
Шаг 4:
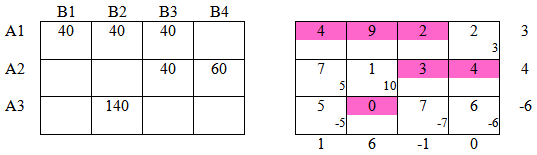
Среди оценочных значений нет отрицательных, следовательно решение оптимально.
S4 = 40 · 4 + 40 · 9 + 40 · 2 + 40 · 3 + 60 · 4 + 140 · 0 = 960 < S3
Задача решена, получен оптимальный план перевозок.
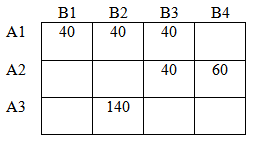
Открытая транспортная задача - пример 2:
Решить открытую транспортную задачу с исходными данными:
Общие потребности (спрос) = 40 + 40 + 20 = 100
Общие запасы (предложение) = 20 + 30 + 40 + 20 = 110
Видим, что предложение превышает над спросом.
Следовательно добавляем фиктивного потребителя В4 с потребностями 110 - 100 = 10.
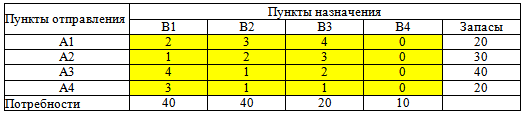
Получили закрытую транспортную задачу: спрос = предложению.
Практическая работа №9
Тема: Целочисленное программирование
Цель урока:
· изучить понятие целочисленного программирования;
· развить навыки решения транспортных задач при помощи метода потенциалов;
· Развивать умения применять формулируемые знания в новых ситуациях;
· Воспитывать самоанализ в новых ситуациях.
Оборудование:
· Компьютеры;
· Программа AutoCAD;
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
- понятие целочисленного программирования;
- методы решения задач целочисленного программирования.
Студент должен уметь:
- применять различные методы для решения задач целочисленного программирования.
Вопросы для повторения
1. Что такое целочисленное программирование?
2. В каких случаях необходимо применение целочисленного программирования?
3. Чем целочисленное программирование отличается от линейного программирования?
4. Какими методами решаются задачи целочисленного программирования?
Ход работы:
Обычно в задачах линейного программирования не требуется, чтобы координаты плана были целыми числами. Однако в практике часто приходится сталкиваться с задачами, в которых координаты оптимальных планов должны быть целыми числами, и такие задачи называются задачами целочисленного программирования. При решении задач линейного программирования графическим методом и симплекс-методом нет гарантий, что координаты оптимального плана будут целыми числами.
В некоторых случаях допускается округление результатов. Например, если в оптимальном плане предусмотрено, что следует произвести 499683,3 автомашины, то экономически обосновано округление результата до 499683 или даже до 500000.
Существуют однако задачи, в которых подобное округление может создать большую ошибку. Например, если в оптимальном плане предусмотрено, что следует построить 0,67 заводов, то формальное округление до 0 или 1 недопустимо.
Поэтому большое практическое значение имеют методы решения задач линейного программирования, с помощью которых можно найти оптимальный план, координаты которого - целые числа. Задачи целочисленного программирования решаются именно такими методами.
Если задача целочисленного программирования задана в канонической форме, она формулируется следующим образом:
найти максимум функции цели (линейной формы)
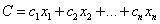
при системе ограничений
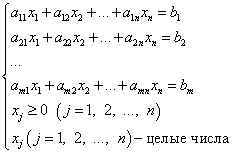
Таким образом, задача целочисленного программирования и соответствующая задача линейного программирования отличаются только условием целочисленности неизвестных.
Как и в задачах линейного программирования, в задачах целочисленного программирования требуется, чтобы оптимальный план максимизировал функцию цели (линейную форму).
Практическая работа №10
Тема: Построение структурной модели
Цель урока:
· развить навыки построения структурных моделей;
· Развивать умения применять формулируемые знания в новых ситуациях;
· Воспитывать самоанализ в новых ситуациях.
Оборудование:
· Компьютеры;
· Программа AutoCAD;
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
- понятие структурного моделирования;
- способы построения структурных моделей.
Студент должен уметь:
- создавать структурные модели.
Вопросы для повторения
1. Какие компьютерные программы используются при построении структурных моделей?
2. Какие геометрические элементы используются для построения структурных моделей?
3. Что такое граф классификации?
Ход работы:
Построение структурных моделей
Пример: Используя графические средства, воспроизведите схему, отражающую состав и структуру танкового батальона. Подсчитайте количество танков в роте и общее количество танков в батальоне.
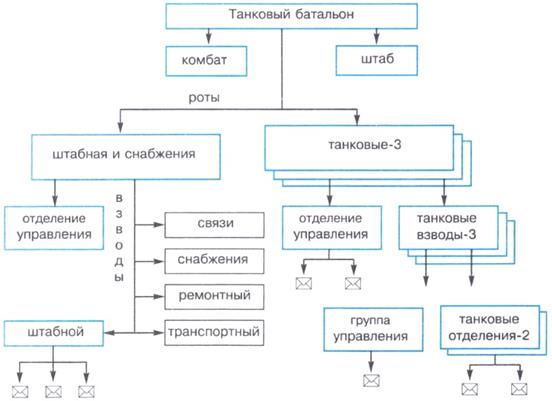
Задание:
Постройте граф, отображающий состав и структуру мотопехотного батальона (армия ФРГ образца 1970 г.) по следующему описанию.
Батальон на БМП (боевых машинах пехоты) имел численность 764 человека. Во главе батальона стоял командир, которому подчинялись штаб и 5 рот: штабная и снабжения, минометная и три мотопехотные. Рота штабная и снабжения состояла из управления и трех взводов: штабного, связи и снабжения. В штабном взводе было четыре отделения: штабное, мотоциклистов, транспортное и разведывательное. Во взводе связи было три отделения радиосвязи и два отделения проводной связи. Во взводе снабжения было четыре отделения: материально-технического обеспечения, продовольственного снабжения, транспортное и санитарное.
Минометная рота состояла из управления, двух отделений передового наблюдения, отделения обеспечения и шести расчетов 120-мм минометов.
Каждая мотопехотная рота (163 чел.) имела в своем составе три мотопехотных взвода по 48 чел. Каждый взвод состоял из группы управления и четырех мотопехотных отделений по 10 чел. Отделение делилось на две группы: первая — командир машины, наводчик-оператор (БМП «Мардер» оснащался пушкой калибра 20 мм и двумя пулеметами) и механик-водитель; вторая — командир отделения, пулеметчик, гранатометчик, огнеметчик и три стрелка.
Пример: Используя графические средства, воспроизведите схему, отражающую классификацию геометрических объектов.
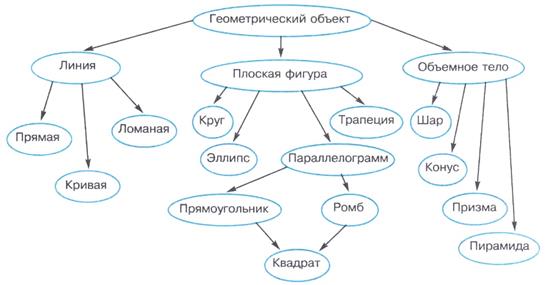
Задания:
1. Постройте граф классификации биологической системы по следующему описанию.
Согласно биологической классификации, выделяют три империи (надцарства): археобактерии, эукариоты и прокариоты. К империи эукариотов относятся царства грибов, растений и животных. К царству животных относятся типы членистоногих, моллюсков, иглокожих, кишечнополостных, хордовых и др. К типу хордовых относятся классы рыб, амфибий, рептилий, млекопитающих, птиц. К классу млекопитающих относятся отряды китов, ластоногих, хищных, грызунов, копытных и др. К отряду хищных относятся семейства медвежьих, енотовых, псовых, виверровых, кошачьих и др. К семейству псовых относятся роды лисиц, енотовидных собак, собак, фенеков, песцов и др. К роду собак относятся виды собак домашних, волков, шакалов, койотов. К виду собак домашних относятся овчарки, спаниели, водолазы, сенбер-нары, доги, болонки и др.
2. Постройте граф классификации в русском языке по следующему описанию.
Предложения в русском языке классифицируются по составу, по интонации и по цели высказывания. По составу предложения делятся на нераспространенные и распространенные. Нераспространенные предложения состоят только из двух членов: подлежащего и сказуемого. Пример нераспространенного предложения: «Птицы прилетели». Распространенные предложения состоят из подлежащего, сказуемого и второстепенных членов предложения. Пример распространенного предложения: «Ранней весной прилетели первые птицы».
По интонации предложения делятся на восклицательные («Пришла весна!») и невосклицательные («Пришла весна.»).
По цели высказывания предложения делятся на повествовательные, вопросительные и побудительные. Повествовательное предложение: «Мы собрали много грибов и ягод.». Вопросительное предложение: «Вы собрали много грибов и ягод?». Побудительное предложение: «Собирайте грибы и ягоды!».
Практическая работа №11
Тема: Построение сетевой модели
Цель урока:
§ Ознакомить студентов с методикой постановки задач сетевого планирования и управления (СПУ) и методами их решения.
Оборудование:
· Компьютеры;
· Программа AutoCAD;
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
§ метод сведения словесного описания плана выполнения комплекса работ к сетевой модели.
Студент должен уметь:
§ определять порядок выполнения сложных разработок, включающих большое число взаимосвязанных работ, требующих многочисленных исполнителей и значительных материальных затрат.
Вопросы для повторения
1. Что представляет собой сетевая модель?
2. Дайте определения основных понятий теории графов.
3. Что представляют собой графы, орграфы?
4. Дать характеристику сетевого графика.
5. Что представляет собой критический путь и каковы методы определения критического пути?
6. Как определить резервы сетевого графика?
7. Каким образом на сетевом графике представляются выполняемые работы, события?
8. Что называется упорядочением или ранжировкой работ при сетевом планировании?
9. Как определяется резерв времени при выполнении работ?
Ход работы:
Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. Отличительной особенностью сетевой модели является четкое определение всех временных взаимосвязей предстоящих работ. Главными элементами сетевой модели являются события и работы.
Термин работа используется в СПУ в широком смысле. Во-первых, это действительная работа – протяженный во времени процесс, требующий затрат ресурсов (например, сборка изделии, испытание прибора и т.п.). Каждая действительная работа должна быть конкретной, четко описанной и иметь ответственного исполнителя.
Во-вторых, это ожидание – протяженный во времени процесс не требующий затрат труда (например, процесс сушки после по краски, старения металла, твердения бетона и т.п.).
В-третьих, это зависимость, или фиктивная работа – логическая связь между двумя или несколькими работами (событиями), не требующими затрат труда, материальных ресурсов или времени. Она указывает, что возможность одной работы непосредственно зависит от результатов другой. Естественно, что продолжительность фиктивной работы принимается равной нулю.
Событие – это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. После дующие работы могут начаться только тогда, когда событие свершится. Отсюда двойственный характер события: для всех непосредственно предшествующих ему работ оно является конечным, а для всех непосредственно следующих за ним – начальным. При этом предполагается, что событие не имеет продолжительности и свершается как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ.
Среди событий сетевой модели выделяют исходное и завершающее события. Исходное событие не имеет предшествующих работ и событий, относящихся к представленному в модели комплексу работ. Завершающее событие не имеет последующих работ и событий.
1. Составление перечня работ.
События на сетевом графике (или, как еще говорят, на графе) изображаются кружками (вершинами графа), а работы – стрелками
(ориентированными дугами), показывающими связь между работами.
Сетевой график дает наглядное представление о порядке выполнения работ, что дает возможность наиболее рационально распорядиться имеющимися трудовыми и материальными ресурсами.
Первый шаг в построении сетевого графика состоит в расчленении всего комплекса на отдельные работы или операции. Каждая работа связана с затратами времени, а значит, имеет свое начало и конец. Моменты начала и окончания работы должны легко определяться.
Перечень работ обычно составляют лица, компетентные в данном конкретном проекте (эксперты).
Одновременно с составлением перечня работ определяются ограничительные условия на их выполнение: длительность каждой работы, средства на ее выполнение, "интенсивность, а также перечень непосредственно предшествующих работ, выполнение которых является необходимым для начала данной работы. Все эти данные заносятся в таблицу, в рассматриваемом примере таблица содержит 16 работ.
Исходные данные для сетевого планирования Таблица 1
| Вид работы | Длительность, мес. | Средства, тыс. руб. | Интенсивность, в чел./мес. | Непосредственно предшествующие работы |
| A | 2,0 | — | ||
| B | 13,0 | А, С, D | ||
| C | 5,0 | — | ||
| D | 5,0 | — | ||
| E | 2,0 | — | ||
| F | 12,0 | D, E | ||
| G | 5,0 | F | ||
| Y | 1,0 | C | ||
| I | 4,0 | B, G, N | ||
| K | 1,0 | C | ||
| L | 3,0 | H | ||
| M | 1,0 | H | ||
| N | 0,5 | A, D | ||
| P | 5,0 | F | ||
| Q | 15,0 | — | ||
| R | 5,0 | Q |
Одновременно с составлением перечня работ определяются ограничительные условия на их выполнение: длительность каждой работы, средства на ее выполнение, "интенсивность, а также перечень непосредственно предшествующих работ, выполнение которых является необходимым для начала данной работы. Все эти данные заносятся в таблицу, в рассматриваемом примере таблица содержащит 16 работ.
2. Упорядочение (ранжировка) работ.
Таблица имеет тот недостаток, что порядок работ в ней носит до некоторой степени случайный характер. Из таблицы не ясно, какие работы являются более важными, а следовательно, не видно, на каких работах нужно сосредоточить основное внимание при выполнении всего комплекса.
С целью устранения этого недостатка отдельным работам удобно приписывать веса, отражающие степень важности этих работ и в значительной степени предопределяющие порядок, в котором должны выполняться работы. Приписывание весов представляет собой упорядочение или ранжировку работ
Примеры выполнения заданий
Задача 1
Определить критический путь и ранний срок выполнения завершающего события по сетевому графику, представленному на рис. 1.
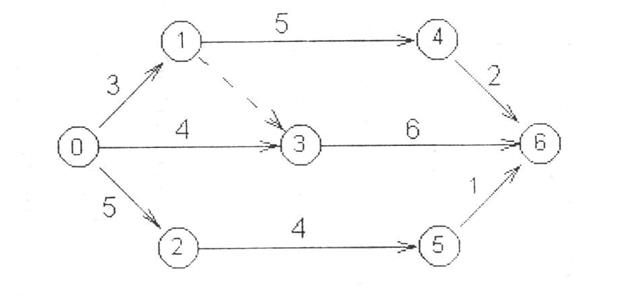
Рис. 1.
Решение.
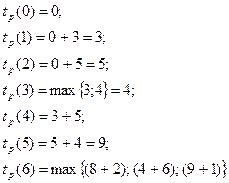
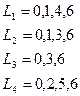
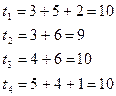
Из 4-х возможных полных путей три оказались критические.
Ранний срок выполнения проекта – 10 недель.
Задача 2.
Определить критический путь в сетевом графике на рис.2, где над ребрами проставлено время, необходимое для выполнения соответствующих работ.
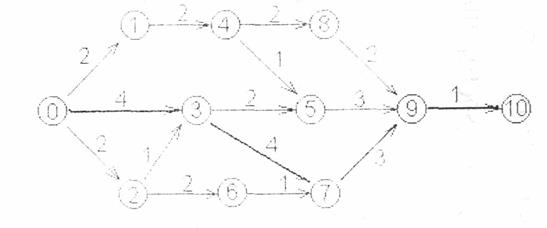
Рис.2.
Составим всевозможные полные пути и найдем их протяженность.
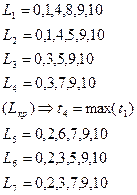
Критический путь проходит через работы 0,3,7,9,10.
Задача 3.
Определить резервы времени для каждого события сетевой модели на рис. 3.
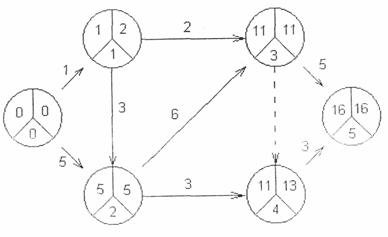
Рис.3.
1. Найдем ранние сроки наступления событий:
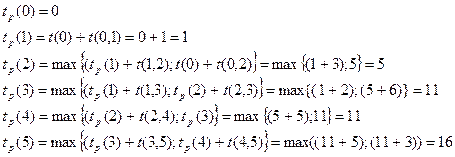
1. Для завершающего события 5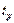 
(5)= 
.
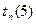2. Найдем поздние сроки наступления событий:
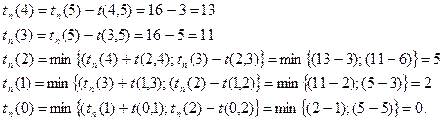
При расчете коэффициентов напряженности целесообразно пользоваться сетевым графиком (рис.3).
Для работ критического пути (0,2); (2,3); (3,5)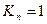 
. Для других работ:
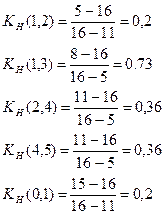
Анализ результатов расчетов коэффициентов напряженности позволяет утверждать, что оптимизация сетевой модели возможна, в основном, за счет двух работ: (0, 1) и (1, 2).
Задача 4.
Структура сетевой модели и оценки продолжительности работ (в сутках) заданы в таблице.
Требуется:
а) получить все характеристики сетевой модели;
б) оценить вероятность выполнения всего комплекса работ (проекта) за 37 и за 30 дней;
в) оценить максимально возможный срок выполнения проекта с надежностью 95%.
Для решения поставленной задачи воспользуемся вспомогательной расчетной таблицей.
Первые три столбца – исходные данные, последние два – расчетные данные по формулам вероятностных оценок ожидаемого времени выполнения работ ( с весом 3 для оптимистической оценки и весом 2 пессимистической) и ожидаемой дисперсии.
Например:
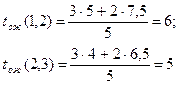
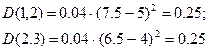
Составим сетевой график (рис. 4 ) и найдем критический путь
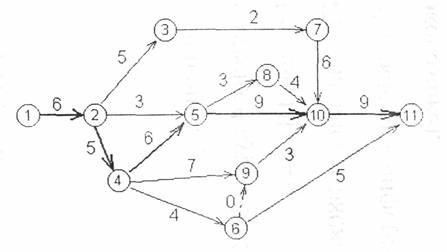
Рис. 4.
Вероятность оценки продолжительности работ
| Работа (i, j) | Продолжительность | Ожидаемая продолжительность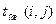 
| Дисперсия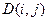 
| |
| 
| |||
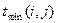
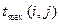
| (1,2) | 7.5 | 0.25 | ||
| (2.3) | 6.5 | 0.25 | ||
| (2.4) | 0.36 | |||
| (2.5) | 5.5 | 0.81 | ||
| (3.7) | 0.5 | 3.5 | 0.36 | |
| (4.5) | 7.5 | 0.25 | ||
| (4.6) | 5.5 | 0.25 | ||
| (4.9) | 1.00 | |||
| (5.8) | 4.5 | 0.25 | ||
| (5.10) | 1.00 | |||
| (6.9) | 0.00 | |||
| (6.11) | 1.00 | |||
| (7.10) | 1.00 | |||
| (8.10) | 1.00 | |||
| (9.10) | 1.00 | |||
| (10.11) | 10.5 | 0.25 |
Его продолжительность равна: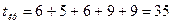 
дней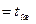 
.
Дисперсия критического пути:
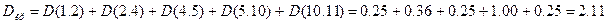Среднеквадратичное отклонение: 
.
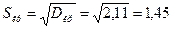Тогда: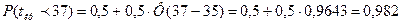 
.
.
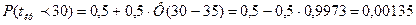Таким образом, вероятность того, что весь комплекс работ будет выполнен не более, чем за 37 дней составляет 98,2%, в то время, как вероятность выполнения за 30 дней всего 0,1%.
Для решения второй задачи по таблице Лапласа найдем значение Z по заданной вероятности 95%:
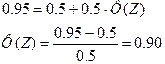
По таблице Z=1.65
Тогда
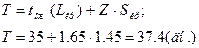
Следовательно, максимальный срок выполнения всего проекта при заданном уровне вероятности 95% составляет 37,4 дней.
Задание к практическому занятию:
Базовый уровень:
Задания 1 - 10
В заданиях ( по вариантам 1 - 10) рассматривается задача.
При разработке проекта водоносной башни было выделено станций – событий 0, 1, 2, 3, 4, 5, 6, 7 и 15 связывающих их путей – работ, с указанием их пропускной способности. Построить 1) сетевой график потоков; 2) найти несколько полных путей; 3) построить линейную диаграмму и по ней определить критический путь.
Варианты заданий
| время t | ||||||||||
| t(0.1) | ||||||||||
| t (0.2) | ||||||||||
| t (0.3) | ||||||||||
| t (1.2) | ||||||||||
| t (1.4) | ||||||||||
| t (2.3) | ||||||||||
| t (2.4) | ||||||||||
| t (2.5) | ||||||||||
| t (2.6) | ||||||||||
| t (3.5) | ||||||||||
| t (4.6) | ||||||||||
| t (4.7) | ||||||||||
| t (5.6) | ||||||||||
| t (5.7) | ||||||||||
| t (7.7) |
Задание 11. Перевод магазина на самообслуживание
Построить сетевой график работ. Определить критический путь. Рассчитать таблицу резервов времени.
Работа Содержание работы Длительность
(1,2) Изучение новых образцов торгового оборудования 1
(1,3) Экономическое обоснование мероприятий, составление
и согласование смет, открытие финансирования 50
(2,4) Разработка технического задания на выполнение
чертежей оборудования. Изготовление чертежей
проектной организацией 120
(2,3) Составление проекта расположения оборудования.
Консультации по технической эстетике. Корректировка,
согласование проекта планировки. 40
(3,4) Составление сводного заказа на оборудование 10 (3,7) Ознакомление всех работников с планами мероприятий
и проектами. Разработка рабочего проекта планировки. 20 (3,8) Определение оптимального числа работников секций по
новой схеме. Утверждение штатного расписания. 15
(4,5) Капитальный ремонт и переделка отдельных стендов
и оборудования. 20 (4,6) Изготовление и поставка оборудования, проверка
комплектности. 50
(4,9) Сборка отдельных конструкций оборудования в
подсобных помещениях. 10
(5,9) Монтаж отремонтированных стендов и оборудования,
выкладка товаров. 5
(6,9) Формирование бригад для оперативной реконструкции
торговых залов. Инструктаж ответственных лиц. 5
(7,8) Ознакомление работников с новыми средствами рекламы 3
(7,9) Заказ на изготовление новых рекламных средств и
аннотаций на товары. 10
(8,9) Занятия с продавцами в школах торгового качества 15
Задание 12. Оперативная реконструкция обувной секции.
Построить сетевой график работ. Определить критический путь. Рассчитать таблицу резервов времени.
Работа Содержание работы Длительность
(1,2) Вывоз товара, разбор горок отдела 3
(2,3) Транспортировка горок в подсобное помещение 1.5
(2,4) Разработка деревянных шкафов 2
(2,5) Вывоз нового оборудования 3
(3,5) Вывоз сидений 0.5
(4,7) Транспортировка деревянных шкафов в подсобные 2
помещения.
(4,8) Установка кассовых кабин 3
(5,6) Монтаж нового оборудования 2
(6,8) Расстановка оборудования по новой планировке 3
(7,8) Транспортировка стеклянных шкафов в подсобные
помещения. 2
(7,11) Разбраковка 3
(8,9) Ввоз товаров 1
(8,10) Подключение касс 1.5
(9,10) Выкладка товаров 1
Задание 13. Планирование строительства универсальной оптовой базы.
Построить сетевой график работ. Определить критический путь. Рассчитать таблицу резервов времени.
Работа Содержание работы Длительность
(1,2) Выбор участка строительства 30
(1,3) Экономическое обоснование строительств 10
(1,5) Выбор подрядчика 15
(2,6) Характеристика зоны размещения, составление
акта по выбору площадки строительства 10
(2,7) Выделение участка муниципалитетом 10
(3,4) Определение сметной стоимости работ и выделение
средств 25
(3,6) Заказ и выполнение типового проекта 20
(4,7) Открытие счета в банке 2
(4,5) Сообщение подрядчику об открытии счета 2
(5,7) Заключение договора с подрядчиком 15
(6,7) Привязка проекта к участку застройки 45
(7,8) Разработка проектов организации и производства
строительных работ 35
Задание 14. Разработка плана развития торговой сети
Построить сетевой график работ. Определить критический путь. Рассчитать таблицу резервов времени.
Работа Содержание работы Длительность
(1,2) Изучение материалов анализа торговой сети за
отчетный период 3
(1,3) Изучение соответствия структуры торговой сети
объему и структуре товарооборота. 2
(1,4) Изучение степени обеспеченности населения
торговой сетью. 1
(2,3) Определение торговой площади, пригодной для
дальнейшей эксплуатации. 4
(2,5) Расчет показателей эффективности использования
торговой сети. 2
(2,6) Анализ технического совещания торговых предприятий 4
(3,4) Расчет коэффициента дифференциации нормативов
площади по группам населенных пунктов 2
(3,5) Определение нормативов торговой площади на 1000 2
жителей
(4,5) Сопоставление фактической обеспеченности
населения торговой сети с нормативами. 1
(5,6) Расчет общей потребности в торговой сети 4
(5,7) Анализ типов розничных предприятий 2
(6,7) Определение возможного введения и выбытия торговой
площади. 1
(7,8) Определение площади нового строительства 4
Задание15. Строительство контейнерной площадки для отгрузки
Овощей.
Построить сетевой график работ. Определить критический путь. Рассчитать таблицу резервов времени.
Работа Содержание работы Длительность
(1,2) Экономическое обоснование целесообразностей
строительства 6
(2,3) Разработка проектно-сметной документации 20
(3,4) Строительство контейнерных площадок в совхозах 30
(3,6) Подборка кадров для работы на контейнерных
площадках 10
(3,7) Заявка на оборудование 2
(3,9) Строительство склада перевалки 20
(3,11) Строительство контейнерной площадки при
железнодорожной станции 40
(4,5) Изготовление необходимого количества контейнеров 15
(5,11) Завоз контейнеров в совхозы 5
(6,11) Обучение кадров 15
(7,8) Завоз оборудования 3
(8,10) Строительство склада для хранения контейнеров 20
(9,11) Строительство участка железной дороги от
контейнерной площадки до склада 30
(10,11) Монтаж оборудования 10
Практическая работа №12
Тема: Построение табличной модели
Цель урока:
§ Изучить возможности электронных таблиц, способы ввода и редактирования данных в табличном виде.
Оборудование:
· Компьютеры;
· Программа Microsoft EXCEL;
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
§ Назначение электронных таблиц;
§ Способы ввода данных;
§ Использование формульных выражений.
Студент должен уметь:
§ Проводить расчёты над данными;
§ Выполнять построение диаграмм на основе табличных данных;
§ Проводить анализ данных.
Вопросы для повторения
1. Что представляет собой графический интерфейс Excel?
2. Какие документы, и с каким расширением создаются документы в Excel?
3. Какие действия производят с рабочими листами?
4. Как производят ввод формул в электронных таблицах?
5. Что такое автозаполнение?
6. Что такое адрес ячейки?
Ход работы:
1. Электронные таблицы
Электронные таблицы – это специальные программы, предназначенные для работы с данными в табличной форме:
· Для проведения расчетов над данными,
· Для построения диаграмм на основе табличных данных,
· Для сортировки и поиска данных на основе определенного критерия,
· Для проведения анализа данных и просчета сценариев типа «что, если?»,
· Для создания баз данных,
· Для печати таблиц и их графического представления.
Первые ЭТ появились в 1979 году.
2. Назначение.
ЭТ предназначены для экономистов, бухгалтеров, инженеров, научных работников – всех тех, кому приходится работать с большими массивами числовой информации.
3. Microsoft EXCEL
На сегодняшний день самой популярной ЭТ является Microsoft EXCEL. Эта программа входит в состав Microsoft OFFICE. Название EXCEL произошло от Executable Cells – исчисляемые ячейки. Хотя некоторые утверждают, что от французского слова Excellent – великолепно.
4. Загрузка Microsoft EXCEL
Загрузка Microsoft EXCEL осуществляется так же, как и WORD:
Пуск ð Программы ð Microsoft EXCEL.
Вид экрана
Вид экрана стандартный для приложений WINDOWS:
· Строка заголовка, в которой содержится название программы и текущего документа.
· Строка меню с основными командами.
· Панели инструментов – Стандартная, Форматирования и Строка формул.
· Рабочее поле, которое состоит из ячеек. Каждая ячейка имеет свой адрес: имя столбца и номер строки, на пересечении которых она находится. Например: А1, С234, Р55. Столбцов всего 256 (последний IV), строк – 65636.
· Слева и внизу экрана находятся полосы прокрутки. Слева от нижней полосы прокрутки находятся вкладки с названиями рабочих листов. Т.о., мы видим только кусок огромной таблицы, которая формируется в памяти ПК.
6. Документы EXCEL
Документы, которые создаются с помощью EXCEL, называются рабочими книгами и имеют расширение . XLS. Новая рабочая книга имеет три рабочих листа, которые называются ЛИСТ1, ЛИСТ2 и ЛИСТ3. Эти названия указаны на ярлычках листов в нижней части экрана. Для перехода на другой лист нужно щелкнуть на названии этого листа. На рабочем листе могут располагаться
· таблицы данных,
· диаграммы (в качестве элемента таблицы или на отдельном листе).
Действия с рабочими листами:
· Переименование рабочего листа. Установить указатель мыши на корешок рабочего листа и два раза щелкнуть левой клавишей или вызвать контекстное меню и выбрать команду Переименовать.
· Вставка рабочего листа. Выделить ярлычок листа, перед которым нужно вставить новый лист, Вставка ê Лист, или с помощью контекстного меню.
· Удаление рабочего листа. Выделить ярлычок листа, Правка ê Удалить, или с помощью контекстного меню.
· Перемещение и копирование рабочего листа. Выделить ярлычок листа и перетащить на нужное место (с нажатой клавишей CTRL – скопировать) или через буфер обмена.
7. Ячейки и диапазоны ячеек.
Рабочее поле состоит из строк и столбцов. Строки нумеруются числами от 1 до 65536. Столбцы обозначаются латинскими буквами: А, В, С, …, АА, АВ, … , IV, всего – 256. На пересечении строки и столбца находится ячейка. Каждая ячейка имеет свой адрес: имя столбца и номер строки, на пересечении которых она находится. Например, А1, СВ234, Р55.
Для работы с несколькими ячейками их удобно объединять их в «диапазоны».
Диапазон – это ячейки, расположенные в виде прямоугольника. Например, А3, А4, А5, В3, В4, В5. Для записи диапазона используется «:»: А3:В5
15:15 15.
8:20 – все ячейки в строках с 8 по 20.
А:А – все ячейки в столбце А.
Н:Р – все ячейки в столбцах с Н по Р.
В адрес ячейки можно включать имя рабочего листа: Лист8!А3:В6.
Выделение ячеек.
| Что выделяем | Действия |
| Одну ячейку | Щелчок на ней или перемещаем выделения клавишами со стрелками. |
| Строку | Щелчок на номере строки. |
| Столбец | Щелчок на имени столбца. |
| Диапазон ячеек | Протянуть указатель мыши от левого верхнего угла диапазона к правому нижнему. |
| Несколько диапазонов | Выделить первый, нажать SCHIFT+F8, выделить следующий. |
| Всю таблицу | Щелчок на кнопке «Выделить все» (пустая кнопка слева от имен столбцов) |
Можно изменять ширину столбцов и высоту строк перетаскиванием границ между ними.
Работа с диапазонами.
Удаление содержимого.
· Выделить ячейку или диапазон;
· а) ухватиться за маркер заполнения, перетащить вверх или влево и отпустить кнопку мыши;
б) нажать <DEL>;
в) Правка ð Очистить.
Копирование.
· Копирование содержимого ячейки в другую ячейку.
· Копирование содержимого ячейки в диапазон ячеек. При этом содержимое исходной ячейки копируется в каждую ячейку соответствующего диапазона.
· Копирование содержимого диапазона в другой диапазон. При этом оба диапазона должны иметь одинаковые размеры.
!!! При копировании ячейки происходит копирование содержимого ячейки, атрибутов форматирования и примечаний (если оно есть), формулы модифицируются.
Способы копирования
1. С помощью буфера обмена.
Выделить.
<Ctrl+C>, Кнопка <Копировать> на Панели инструментов, Правка ð Копировать, Контекстное меню.
Поместить табличный курсор в левый верхний угол диапазона назначения и выполнить операцию вставки (<Ctrl +V> Кнопка <Вставить>, Правка ð Вставить, Контекстное меню)
!!! При вставке из БО все значения, находящиеся в ячейках диапазона назначения стираются без всякого предупреждения (в случае необходимости применить отмену)
2. Перетаскивание D&D
Выделить.
Переместить указатель мыши к рамке выделения, когда он превратиться в стрелку, нажать <Ctrl> (к указателю добавиться знак +), перетащить на новое место.
!!! Если указатель мыши не принимает форму стрелки при перетаскивании, то Сервис - Параметры - вкладка Правка - отметить Перетаскивание ячеек.
Перемещение
Перемещение диапазона выполняется аналогично копированию (без <Ctrl> при перетаскивании и команда Вырезать для буфера обмена).
!!! При перемещении ячейки с формулой, ссылки (адреса ячеек), имеющиеся в формуле, не изменяются.
!!! Очень удобно пользоваться специальным перетаскиванием (с нажатой правой клавишей мыши). Это дает дополнительные возможности, которые можно выбрать из меню.
Дата: 2019-12-10, просмотров: 838.
