Дискретная случайная величина может быть задана табличной
зависимостью:
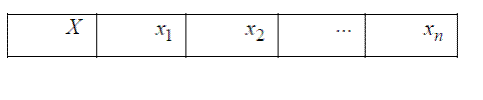
Здесь p j – вероятность того, что дискретная случайная величина X примет
значение x j . При этом p1 + p2 +... + p n =1. Разделим интервал (0,1) на n отрезков,
длины которых равны заданным вероятностям. Если случайное число z ,
вырабатываемое датчиком случайных чисел, равномерно распределенных в
интервале (0,1), попадет в интервал p k , то случайная величина X примет
значение x k . Таким образом, при моделировании дискретных случайных величин
фактически используется та же процедура, что и при моделировании полной
группы несовместных событий.
Моделирование непрерывной случайной величины
Приведем способы моделирования непрерывных случайных чисел (на рис.
4 показаны формы распределения вероятностей) [23-24].
1. Показательное распределение
1
x ln(z)
ë
= − ,
где x - случайная величина, распределенная по показательному закону;
ë - интенсивность потока (среднее значение 1 ì
ë
= );
z - случайная величина, равномерно распределенная на интервале (0,1).
В Excel данное вычисление выглядит следующим образом (пусть в ячейке
А1 дано среднее значение, а в А2 - результат)
А2=-А1*LN(СЛЧИС()).
2. Равномерное распределение на интервале ( a,b )
x = a + z(b − a) ,
x = x cp + Äx(z − 0,5) ,
где x - случайная величина, распределенная по равномерному закону;
a и b- нижняя и верхняя границы интервала ( a,b) соответственно;
x ср - среднее значение интервала ( a,b);
Äx - величина интервала ( a,b);
z - случайная величина, равномерно распределенная на интервале (0,1).
В Excel это реализуется посредством формулы (пусть в ячейке А1 дана
нижняя граница; в ячейке А2 – верхняя граница, а в А3 - результат)
А3=А1+СЛЧИС()*(А2-А1)
3. Нормальное распределение
Процедура розыгрыша нормально распределенной случайной величины
заключается в следующем.
• Сложим 12 случайных величин z i с равномерным распределением в
интервале (0,1), т. е. составим сумму
12
1
i
i
v z
=
=Ó .
• Нормируем и центрируем случайную величину v , т. е. перейдем к величине
ç = v − 6.
• От нормированной и центрированной величины ç перейдем к случайной
величине y , распределенной по нормальному закону, с заданными
параметрами M( y) и ó ( y) по формуле
y = M( y) +ó ( y) ⋅ç ,
где M( y) – известное математическое ожидание случайной величины y ;
ó ( y) – известное среднее квадратическое отклонение случайной величины
y .
Для реализации данного генератора в Excel нужно выполнить следующий
расчет (в ячейке А1 дано среднее значение, А2 – среднее квадратическое
отклонение, а в А3 - результат)
А3=А1+А2*((СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИ
С()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС()+СЛЧИС())-6)).
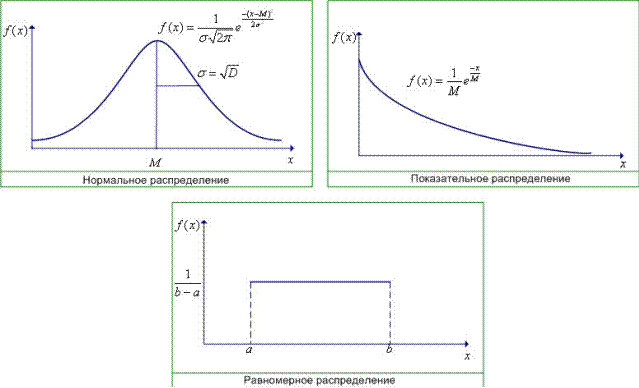
Рис. 4 – Графики законов распределения
Практическая работа № 31
Тема: Моделирование системы массового обслуживания с одним устройством обслуживания.
Цель урока:
· Освоить 3Д-технологии построения ломаного разреза;
· Развивать умения применять формулируемые знания в новых ситуациях;
· Воспитывать самоанализ в новых ситуациях.
Оборудование:
· Компьютеры;
· Программа AutoCAD;
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
· Какой сложный разрез называется ломаным;
· Особенности выполнения ломаного разреза предусмотренные ГОСТ 2.305-68;
· Порядок анализа формы детали.
Студент должен уметь:
· Выполнять построение ломаного разреза;
· Анализировать форму детали;
· Использовать команды для замыкания и выдавливания контура;
· Вычерчивать контур вращения;
· Объединять элементы основания;
· Применять команды вычитания тела.
Вопросы для повторения
1. Что должен содержать чертёж, построенный по 3Д-технологии;
2. Какой сложный разрез называется ломаным?
3. Какой порядок выполнения настроек используется для построения чертежей по 3Д-технологии?
4. Как построить контур выдавливания?
5. Какой порядок замыкания контура?
Ход работы:
Имитационное моделирование систем массового обслуживания В разных областях техники, в организации производства, в экономике и медицине, в социальной сфере, в военном деле и во многих других сферах человеческой деятельности постоянно возникает необходимость решения вероятностных задач, связанных с работой систем массового обслуживания (СМО). Многообразие приложений теории массового обслуживания определяет постоянно растущий интерес к ней, а сложность возникающих задач не позволяет получить исчерпывающие решения на базе аналитических методов. В таких ситуациях часто прибегают к имитационному моделированию. Для имитации подобных систем предназначен язык моделирования GPSS, а также создаются сложные программные системы (ObjectSim, Pigrim [10]), позволяющие реализовать модели систем массового обслуживания с помощью развитой CASEоболочки путем выбора и связи различных строительных блоков. Среди работ, описывающих моделирование СМО с помощью электронных таблиц можно привести следующие - [3-7]. Авторы рассматривают моделирование систем с неограниченным, ограниченным по времени и/или длине очереди ожиданием, которые располагают от 1 до 12 обслуживающими устройствами [7]. При этом различают два основных подхода к моделированию СМО: ориентированный на события и ориентированный на процессы. Событийный подход имеет преимущества в отношении гибкости и эффективности вычислений, однако менее подходит для обучения, поскольку скрывает «жизненный цикл» заявок и является менее понятным на интуитивном уровне. Кроме того, для его реализации требуется управляющая событиями подпрограмма, что приводит к необходимости использования внутреннего языка VBA [11]. Рассмотренные ниже модели будут реализованы с использованием процессно-ориентированного подхода. Рассмотрим структуру СМО. Каждая СМО состоит из определенного числа обслуживающих единиц, которые называются каналами обслуживания. На вход СМО поступает поток требований (заявок). Таким образом, различают следующие элементы СМО: 1. входной поток заявок; 2. очередь; 3. узел обслуживания; 4. выходной поток. На рис. 2.1 указаны эти элементы для следующей СМО: бензоколонка занимается заправкой автомобилей.
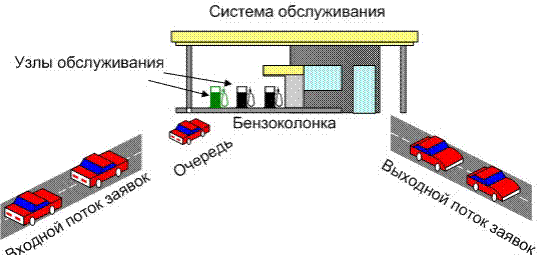
Рис. 2.1 – Пример системы массового обслуживания
Входной поток заявок может быть случайным или детерминированным. В
первом случае время между поступлением двух заявок является случайной
величиной, а во втором – величиной детерминированной (поступление
происходит в соответствие с определенным графиком). Интенсивность потока ë –
частота появления событий, поступающих в СМО в единицу времени. В СМО
может поступать несколько входных потоков, имеющих различные характеристики
(интервал поступления, приоритет и т.д.).
Очередь – место, где поступившие заявки ждут начала обслуживания. В том
случае, если элемент очередь в системе отсутствует, то данная система без
ожидания. Это означает, что в том случае, если в момент поступления заявки все
каналы обслуживания заняты, то эта заявка покидает систему необслуженной.
Очередь может иметь ограниченную или неограниченную длину. Кроме того,
время ожидания в очереди может быть ограничено (говорят, что рассматриваются
нетерпеливые заявки). Следующая характеристика очереди – дисциплина
очереди. Она связана с правилом, в соответствии с которым обслуживаются
клиенты. Различают следующие дисциплины: первый пришел – первый ушел,
первый пришел – последний ушел, а также существуют дисциплины с
приоритетами.
Рассмотрим теперь характеристики средств обслуживания. Системы
обслуживания характеризуются по числу каналов обслуживания (например, если
на рис. 2.1 машины могут быть обслужены несколькими устройствами, то система
будет многоканальной), числу фаз обслуживания. Время обслуживание может
быть случайной величиной или детерминированным.
Также существую системы, в которых обслуженные требования после
некоторой задержки опять поступают на вход. Такие системы называются
замкнутыми.
В качестве показателей эффективности СМО рассматриваются: среднее
время, которое клиент проводит в очереди, средняя длина очереди, среднее
время, которое клиент проводит в системе обслуживания
( TotalTimeSystem
TimeSystem
N
= , где TotalTimeSystem - общее время пребывания в
системе для всех заявок, а N -число заявок), среднее число клиентов в системе
обслуживания, вероятность того, что система окажется свободной и т.д.
Дата: 2019-12-10, просмотров: 524.