Что означают числа в условии транспортной задачи?
Рассмотрим постановку транспортной задачи, т.е. что дано в условии и переведем ее с математического языка на язык, понятный нам.
Это наши "склады" - пункты отправления: два склада с товаром: А1 и А2
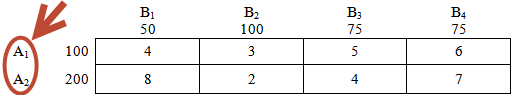
Это объем товара - количество груза, соответственно на складах А1 и А2:
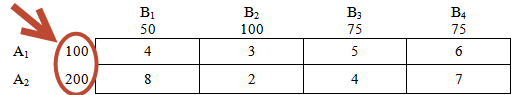
Далее имеем дело с пунктами назначения - с "магазинами". В нашем случае их 4 штуки: В1, В2, В3 и В4.

И соответственно потребности каждого из магазинов - потребности пунктов назначения:

Числа внутри таблицы - матрица стоимостей, или по другому, расценки перевозки 1 единицы груза из соответствующих пунктов. Эти значения также могут интерпритироваться как расстояния между соответствующими пунктами. Подробности — в условии решаемой задачи.

Например, для перевозки 1 единицы груза из пункта отправления ("склада") А2 в пункт назначения ("магазин") В3 надо заплатить 4 условные единицы стоимости, например 4 руб.

Аналогично, мы заплатим 6 рублей за перевозку 1 единицы груза из "склада" А1 в "магазин" В4.

Или та же самая задача может быть задана сразу в более понятном виде:

Возможна текстовая постановка задачи. В этом случае необходимо самим заполнять все ячейки таблицы, исходя из заданных в условии значений.
Далее - Методы определения первоначального плана транспортной задачи.
Методы определения первоначального плана транспортной задачи.
Рассмотрим самый распространенный метод получения опорного плана - метод северо-западного угла.
Называется он так потому, что заполнение таблицы начинается с самой верхней левой (северо-западной) ячейки.
Перед тем, как распределять ресурсы по "магазинам", проверим, равны ли общие потребности имеющимся ресурсам?

Потребности: 50 + 100 + 75 + 75 = 300
Ресурсы: 100 + 200 = 300
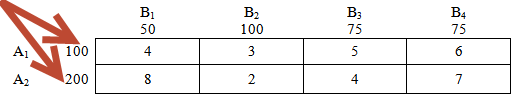
Потребности = Ресурсам
В этом случае говорят, что транспортная задача закрытая. Решение открытой транспортной задачи рассмотрим чуть позже.
Начнем нахождение опорного решения:

Заполним клетку (1;1).
В магазин В1 требуется 50 единиц товара. Со склада А1 отправим в этот магазин 50 единиц.
Потребности магазина В1 выполнены, следовательно, нет необходимости везти туда груз со склада А2.

На складе А1 еще осталось 50 единиц груза. Эти остатки можем направить в магазин В2. Ресурсы склада А1 исчерпаны.

Переходим к складу А2.
Так как потребности магазина В1 выполнены полностью, рассмотрим магазин В2, которому требуется 100-50=50 единиц товара. Направим их туда.

Заметим, на складе А2 осталось еще 200-50=150 единиц груза, которые мы распределим по магазинам В3 и В4, полностью удовлетворяя и их потребности.

Склады пусты!
Потребности магазинов в товаре полностью выполнены!
Получен опорный (первоначальный) план транспортной задачи.

Рассмотрели северо-западный метод построения первоначального плана (опорного решения).
Далее опишем метод минимальных стоимостей получения опорного плана.
Метод минимальных стоимостей получения опорного плана
Суть метода состоим в том, чтобы в первую очередь направлять груз в те пункты, где "расценки" в матрице стоимостей минимальны. Если клеток с наименьшими тарифами несколько, то заполняется любая из них.

Направляем 100 единиц груза из склада А2 в магазин В2.
Остатки на складе А2 — 100 единиц. Потребности магазина В2 выполнены.

Груз со склада А2 отправим в магазин, у которого стоимость перевозки ниже — магазин В3, так как мин(4;7)=4
Размер поставки равен потребности магазина — 75. Остатки со склада 200-100-75=25 перенесем в магазин В4.

Остается только раскидать груз со склада А1 по магазинам: В1 — 50 единиц, В4 — 75-25=50 единиц.

Получили два опорных плана: методом северо-западного угла и методом минимальных стоимостей.
Первый опорный план (по методу северо-западного угла):

Второй опорный план (по методу минимальных стоимостей):

Далее проверим правильность вычисления первоначального плана.
Проверка правильности вычисления первоначального плана
Перед тем как перейти к дальнейшему решению задачи проверим условие:
Правило:
Количество заполненных клеток (базисных клеток) в первоначальном плане ВСЕГДА должно быть равно m + n - 1, где m - количество строк, n - количество столбцов
В нашем случае условие выполняется: 2 + 4 - 1 = 5
Что же делать, если количество заполненных ячеек меньше необходимого?
Подробно об этом с разбором примеров в статье Вырожденность опорного плана транспортной задачи. Как избавиться?
Во избежании случайных вычислительных ошибок проверим, равны ли суммарные значения каждой строки и каждого столбца соответствующим значениям условия.
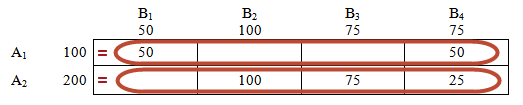
100 = 50 + 50
200 = 100 + 75 + 25
По столбцам:
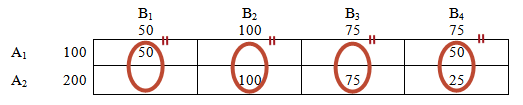
Видим, суммарные значения элементов каждого столбца равны соответствующим потребностям магазинов.
Несмотря на то, что опорные планы разные, оба приведут к одному оптимальному решению или же к решениям, имеющим одну стоимость перевозки.
Далее применим метод потенциалов к обоим опорным планам и сравним получившиеся ответы.
Метод потенциалов решения транспортной задачи - шаг 1.
Описанную ниже последовательность действий будем повторять несколько раз, с каждым шагом приближаясь к оптимальному решению. Начнем с проверки опорного плана на оптимальность.
Выпишем матрицу стоимостей, данную в условии задачи.

| 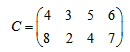
|
Далее строим рядом две таблицы. Размерность таблиц как и в матрице стоимостей:
количество строк = количеству складов, количество столбцов = количеству магазинов.
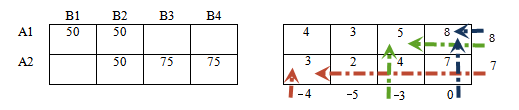
Заполняем первую — левую таблицу в соответствии с полученным опорным планом.

Переходим в правую таблицу.
Переносим из матрицы стоимостей значения, которые соответствуют занятым клеткам левой таблицы.
В матрице стоимости эти значения подчеркнуты.
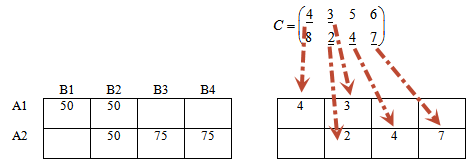
Припишем каждой строке правой таблице потенциалы u1, u2. Каждому столбцу — потенциалы v1, v2, v3, v4.
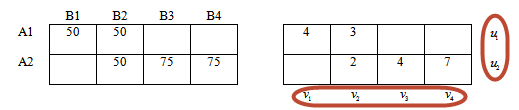
Для вычисления этих потенциалов в некоторых учебниках составляют систему и из нее определяют неизвестные (покажу на данном шаге).
Мы будем определять значения потенциалов непосредственно из правой таблицы.
Составим систему уравнений по следующему правилу:
Каждое из значений в ячейке (правая таблица) равно сумме потенциалов соответствующей строки и соответствующего столбца.
Например: значение 4 находится в 1-й строке и 1-м столбце. Тогда сумма потенциалов 1-й строки (u1) и 1-ого столбца(v1) равна 4.
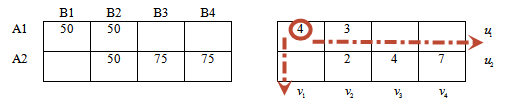
Первое уравнение системы: u1 + v1 = 4
Рассмотрим следующее значение таблицы.
Значение 3 находится в первой строке (потенциал u1), втором столбце (потенциал v2).
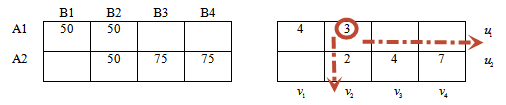
Второе уравнение системы: u1 + v2 = 3
Аналогично для каждого значения таблицы составим уравнение.
Получим систему уравнений:
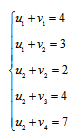
Для того, чтобы система имела единственное решение, примем значение одного из потенциалов равным нулю.
Для удобства в качестве этого потенциала всегда будем брать v4.
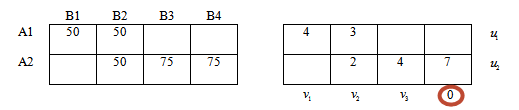
Тогда система уравнений будет выглядеть:
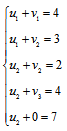
Решим систему уравнений и получим значения потенциалов:
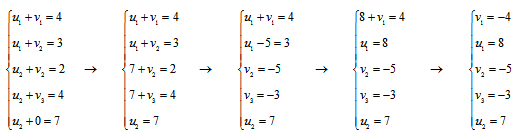
Наглядно:

Так как система очень проста, то значения потенциалов можно получить и устно.
Покажем подробно:
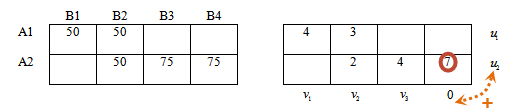
Сумма отмеченных потенциалов равна 7, следовательно, потенциал u2 = 7
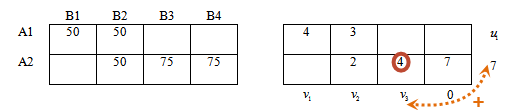
Значение 4 базисной ячейки находится во 2-й строке, 3-м столбце, тогда рассмотрим сумму соответствующих потенциалов.
v3 + 7 = 4 откуда v3 = -3
Далее все аналогично:
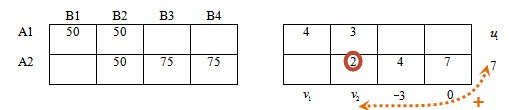
Значение 2 равно сумме потенциалов 2-й строки и 2-го столбца:
2 = v2 + 7 откуда v2 = -5
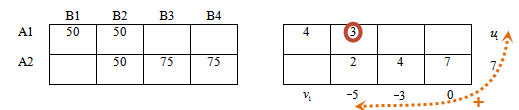
u1 - 5 = 3, откуда u1 = 8
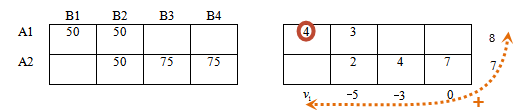
v1 + 8 = 4, откуда v1 = -4
В итоге получили:
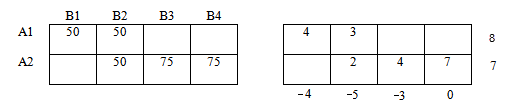
Далее приступим к заполнению пустых ячеек (свободные ячейки) правой таблицы.
Свободные ячейки подчиняются тому же правилу суммирования потенциалов.
Вычислим оценочную матрицу, по которой узнаем, оптимален ли рассматриваемый план.
Из каждого элемента матрицы стоимостей вычтем соответствующий элемент правой таблицы:
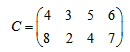
| — | 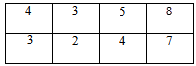
| = | 
|
Получили оценочную матрицу. Заметим, что в базисных ячейках всегда получим нули.
Критерий оптимальности:
Дата: 2019-12-10, просмотров: 447.