Практические работы проводятся после изучения теоретического материала. Студенты должны иметь методические рекомендации по выполнению практических работ и конспекты лекций.
1.3. Критериями оценки результатов работы студентов являются:
ü Уровень усвоения студентом учебного материала;
ü Умение студента использовать теоретические знания при выполнении практических работ;
ü Сформированность ключевых (общенаучных) компетенций;
ü Обоснованность и чёткость изложения материала;
ü Уровень оформления работы.
Анализ результатов
Если практическая работа выполнена в полном объёме и правильно оформлена, то ставится оценка «5».
Если практическая работа выполнена более чем на 75%, то ставится оценка «4».
Если практическая работа выполнена более чем на 60%, то ставится оценка «3».
В противном случае работа не засчитывается.
2. Практические работы по учебной дисциплине компьютерное моделирование
Практическая работа №1
Тема: Построение блок-схемы процесса построения модели.
Цель урока:
· Изучить понятие, назначение и фазы технологического процесса;
· Развивать наблюдательность, логическое мышление, умения применять формулируемые знания в новых ситуациях;
· Воспитывать самоанализ в новых ситуациях.
Оборудование:
· Компьютеры;
· Интернет;
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
· Понятия определений технологического процесса, автоматизации технологического процесса, фазы технологического процесса;
· Составные части технологического процесса;
· Виды технологического процесса.
Студент должен уметь:
· Проектировать различные технологические процессы;
· Составлять структурные схемы технологических процессов.
Вопросы для повторения
1. Что такое производственный процесс?
2. В чём заключается основное достоинство автоматизации технологического процесса?
3. На какие фазы делится технологический процесс?
4. К какой фазе технологического процесса относится сварка?
5. Что такое операция технологического процесса?
6. Какие существуют виды операций?
Ход работы:
Блок-схемы Блок-схема – это представление алгоритма в графической форме. Все команды и действия представлены геометрическими фигурами (блоками). Внутри каждой фигуры вписывается вся информация о тех действиях, которые нужно выполнить. Связи изображены в виде обычных линий со стрелками (при необходимости). Для оформления блок-схем алгоритмов имеется ГОСТ 19.701-90. Он описывает порядок и правила создания их в графической форме, а также основные методы решения. В этой статье приведены основные элементы блок-схем, которые используются при решении задач, например, по информатике. А теперь давайте рассмотрим правила построения.
Основные правила составления блок-схемы Можно выделить такие особенности, которые должны быть у любой блок-схемы:
Обязательно должно присутствовать два блока – «Начало» и «Конец». Причем в единичном экземпляре.
От начального блока до конечного должны быть проведены линии связи.
Из всех блоков, кроме конечного, должны выходить линии потока.
Обязательно должна присутствовать нумерация всех блоков: сверху вниз, слева направо.
Порядковый номер нужно проставлять в левом верхнем углу, делая разрыв начертания.
Все блоки должны быть связаны друг с другом линиями. Именно они должны определять последовательность, с которой выполняются действия.
Если поток движется снизу вверх или справа налево (другими словами, в обратном порядке), то обязательно рисуются стрелки.
Линии делятся на выходящие и входящие. При этом нужно отметить, что одна линия является для одного блока выходящей, а для другого входящей.
От начального блока в схеме линия потока только выходит, так как он является самым первым.
А вот у конечного блока имеется только вход. Это наглядно показано на примерах блок-схем, которые имеются в статье.
Чтобы проще было читать блок-схемы, входящие линии изображаются сверху, а исходящие снизу.
Допускается наличие разрывов в линиях потока. Обязательно они помечаются специальными соединителями.
Для облегчения блок-схемы разрешается всю информацию прописывать в комментариях.
Линейный тип алгоритмов Это самый простой вид, который состоит из определенной последовательности действий, они не зависят от того, какие данные вписаны изначально. Есть несколько команд, которые выполняются однократно и только после того, как будет сделана предшествующая. Линейная блок-схема выглядит таким образом:
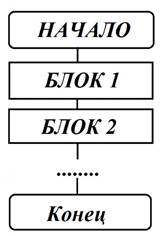
Причем связи могут идти как сверху вниз, так и слева направо. Используется такая блок-схема для записи алгоритмов вычислений по простым формулам, у которых не имеется ограничений на значения переменных, входящих в формулы для расчета. Линейный алгоритм – это составная часть сложных процессов вычисления.
Разветвляющиеся алгоритмы Блок-схемы, построенные по таким алгоритмам, являются более сложными, нежели линейные. Но суть не меняется. Разветвляющийся алгоритм – это процесс, в котором дальнейшее действие зависит от того, как выполняется условие и какое получается решение. Каждое направление действия – это ветвь.
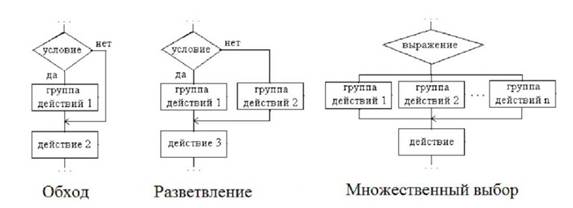
На схемах изображаются блоки, которые называются «Решение». У него имеется два выхода, а внутри прописывается логическое условие. Именно от того, как оно будет выполнено, зависит дальнейшее движение по схеме алгоритма. Можно разделить разветвляющиеся алгоритмы на три группы: «Обход» – при этом одна из веток не имеет операторов. Другими словами, происходит обход нескольких действий другой ветки. «Разветвление» – каждая ветка имеет определенный набор выполняемых действий. «Множественный выбор» – это разветвление, в котором есть несколько веток и каждая содержит в себе определенный набор выполняемых действий. Причем есть одна особенность – выбор направления напрямую зависит от того, какие заданы значения выражений, входящих в алгоритм. Это простые алгоритмы, которые решаются очень просто. Теперь давайте перейдем к более сложным.
Циклический алгоритм Здесь все предельно понятно – циклическая блок-схема представляет алгоритм, в котором многократно повторяются однотипные вычисления. По определению, цикл – это определенная последовательность каких-либо действий, выполняемая многократно (более, чем один раз). И можно выделить несколько типов циклов: У которых известно число повторений действий (их еще называют циклами со счетчиком). У которых число повторений неизвестно – с постусловием и предусловием. Независимо от того, какой тип цикла используется для решения алгоритма, у него обязательно должна присутствовать переменная, при помощи которой происходит выход. Именно она определяет количество повторений цикла. Рабочая часть (тело) цикла – это определенная последовательность действий, которая выполняется на каждом шаге. А теперь более детально рассмотрим все типы циклов, которые могут встретиться при составлении алгоритмов и решении задач по информатике.
Циклы со счетчиками На рисунке изображена простая блок-схема, в которой имеется цикл со счетчиком. Такой тип алгоритмов показывает, что заранее известно количество повторений данного цикла. И это число фиксировано. При этом переменная, считающая число шагов (повторений), так и называется – счетчик. Иногда в учебниках можно встретить иные определения – параметр цикла, управляющая переменная.
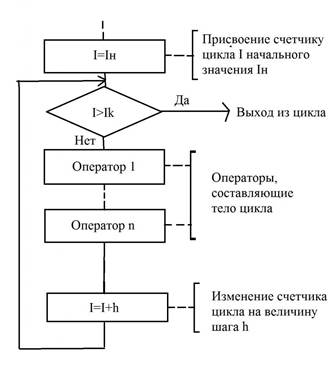
Блок-схема очень наглядно иллюстрирует, как работает цикл со счетчиком. Прежде чем приступить к выполнению первого шага, нужно присвоить начальное значение счетчику – это может быть любое число, оно зависит от конкретного алгоритма. В том случае, когда конечное значение меньше величины счетчика, начнет выполняться определенная группа команд, которые составляют тело цикла. После того, как тело будет выполнено, счетчик меняется на величину шага счетчика, обозначенную буквой h. В том случае, если значение, которое получится, будет меньше конечного, цикл будет продолжаться. И закончится он лишь в тогда, когда конечное значение будет меньше, чем счетчик цикла. Только в этом случае произойдет выполнение того действия, которое следует за циклом.
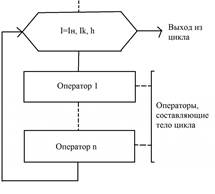
Обычно в обозначениях блок-схем используется блок, который называется «Подготовка». В нем прописывается счетчик, а затем указываются такие данные: начальное и конечное значения, шаг изменения. На блок-схеме это параметры I н, Ik и h, соответственно. В том случае, когда h=1, величину шага не записывают. В остальных случаях делать это обязательно. Необходимо придерживаться простого правила – линия потока должна входить сверху. А линия потока, которая выходит снизу (или справа, в зависимости от конкретного алгоритма), должна показывать переход к последующему оператору. Теперь вы полностью изучили описание блок-схемы, изображенной на рисунке. Можно перейти к дальнейшему изучению. Когда используется цикл со счетчиком, требуется соблюдать определенные условия: В теле не разрешается изменять (принудительно) значение счетчика. Запрещено передавать управление извне оператору тела. Другими словами, войти в цикл можно только из его начала.
Циклы с предусловием Этот тип циклов применяется в тех случаях, когда количество повторений заранее неизвестно. Цикл с предусловием – это тип алгоритма, в котором непосредственно перед началом выполнения тела осуществляется проверка условия, при котором допускается переход к следующему действию. Обратите внимание на то, как изображаются элементы блок-схемы. В том случае, когда условие выполняется (утверждение истинно), происходит переход к началу тела цикла. Непосредственно в нем изменяется значение хотя бы одной переменной, влияющей на значение поставленного условия. Если не придерживаться этого правила, получим «зацикливание». В том случае, если после следующей проверки условия выполнения тела цикла оказывается, что оно ложное, то происходит выход. В блок-схемах алгоритмов допускается осуществлять проверку не истинности, а ложности начального условия. При этом из цикла произойдет выход только в том случае, если значение условия окажется истинным. Оба варианта правильные, их использование зависит от того, какой конкретно удобнее использовать для решения той или иной задачи. Такой тип цикла имеет одну особенность – тело может не выполниться в случае, когда условие ложно или истинно (в зависимости от варианта, который применяется для решения алгоритма). Ниже приведена блок-схема, которая описывает все эти действия:
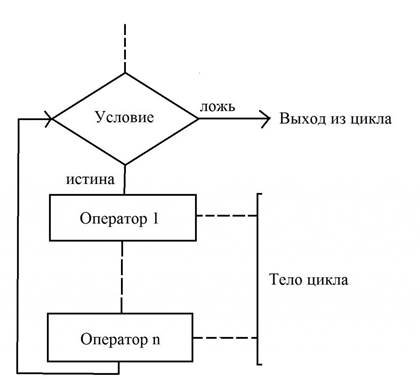
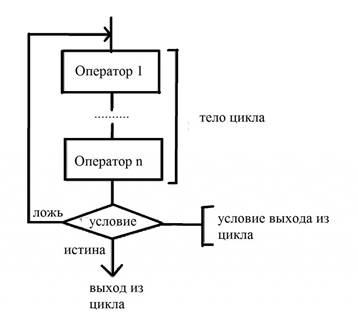
с постусловием? Если внимательно присмотреться, то этот вид циклов чем-то похож на предыдущий. Самостоятельно построить блок-схему, описывающую этот цикл, мы сейчас и попробуем. Особенность заключается в том, что неизвестно заранее число повторений. А условие задается уже после того, как произошел выход из тела. Отсюда видно, что тело, независимо от решения, будет выполняться как минимум один раз. Для наглядности взгляните на блок-схему, описывающую выполнение условия и операторов:
Задание:
Создайте блок-схему:
правописание ь после шипящих
определяем часть речи:
1. если глагол – не пишу ь;
2. если краткое прилагательное – не пишу ь;
3. если наречие, то определяю является ли слово исключением:
3.1. да – не пишу ь (уж, замуж, невтерпёж);
3.2. нет – пишу ь;
4. если существительное, то определяю склонение:
4.1. если 1 или 2 – не пишу ь;
4.2. если 3 – пишу ь.
Учебник Секреты орфографии Граник страница 98
Практическая работа №2
Тема: Построение схемы взаимодействия системы с окружающей средой.
Цель урока:
· познакомиться с различными методами задания координат в программе AutoCAD;
· научиться рисовать отрезки разными способами;
· Развивать умения применять формулируемые знания в новых ситуациях;
· Воспитывать самоанализ в новых ситуациях.
Оборудование:
· Компьютеры;
· Программа AutoCAD;
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
· Методы задания координат;
· Способы рисования отрезков.
Студент должен уметь:
· Научиться рисовать отрезки разными способами;
· Работать в строке состояния;
· Задавать опции размещения;
· Создавать геометрические фигуры при помощи команды Отрезок.
Вопросы для повторения
1. Какие координаты называются абсолютными?
2. Почему первая точка всегда будет в абсолютных декартовых координатах?
3. Какие координаты называются относительными?
4. Какие координаты называются полярными?
Ход работы:
Построение схемы взаимодействия системы и среды.
Укажите входы и выходы системы.
1. Водонагреватель. Служит для подогрева проходящей через него воды.
Входы: электропитание, холодная вода.
Выходы: горячая вода.
2. Телевизор. Устройство для демонстрации изображения со звуковым сопровождением.
Входы: электропитание, сигналы от внешних устройств, управление от пульта.
Выходы: звук изображение, сигналы на внешние устройства.
3. компьютер
4. автомобиль
5. холодильник
6. стиральная машина
7. мультиварка
8. дрон
9. электрочайник
10. пожарная сигнализация
11. лифт в многоквартирном доме
12. робот-пылесос
13. радио-няня
14. радиоуправляемый робот (игрушка)
15. система видео слежения придомовой территории
16. сплит-система
17. домашний кинотеатр
18. система контроля утечки газа
19. пароочиститель
20. увлажнитель воздуха
Практическая работа №3
Тема: Построение математических моделей.
Цель урока:
· Изучить элементы автоматики;
· Развивать умения применять формулируемые знания в новых ситуациях;
· Воспитывать самоанализ в новых ситуациях.
Оборудование:
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
· Классификации элементов автоматики;
· Назначение элементов автоматики.
Студент должен уметь:
· Создавать структурные схемы;
· Уметь классифицировать элементы автоматики.
Вопросы для повторения
1. Как подразделяются элементы автоматики по принципу получения энергии?
2. Как подразделяются элементы автоматики по выполняемым функциям?
3. Какие бывают виды датчиков?
4. Какие бывают виды усилителей?
Ход работы:
Ежедневно люди принимают тысячи решений, отвечая на различные вопросы, начиная от простых «Где пообедать?» до сложных «В каких городах разместить филиалы компании?» Часто процесс принятия решения можно описать аналитически. Предположим, Вы хотите оценить время, затрачиваемое на дорогу от работы до дома, для этого нужно узнать расстояние и разделить его на среднюю скорость передвижения. Получаем количественную модель:
t = S v ,
где S — расстояние,
v — средняя скорость,
t — время в пути.
Эта модель полезна, но, как и любая модель, обладает существенным недостатком: упрощает и идеализирует реальность. Например, в модели не учитывается, что, возвращаясь с работы домой, Вы делаете остановки, чтобы зайти в магазины. Это можно учесть, добавив слагаемое:
t = S v + nR,
где n — планируемое число остановок,
R — среднее время на остановку.
В данной модели имеются постоянные величины: расстояние между домом и офисом; и переменные величины, значениями которых можно управлять: скорость передвижения, число остановок и время посещения магазина. С помощью управляемых переменных можно сократить затрачиваемое время на дорогу. Модели, имеющие переменные величины, при изменении значений которых можно моделировать и получать разные решения, называют моделями принятия решений, а сами переменные называют переменными принятия решений. Цель таких моделей не просто вычислить значение какой-то переменной, а найти минимум или максимум какой-либо функции от переменных принятия решений, например, минимизировать потраченное время, максимизировать прибыль и т. д. Рассмотрим следующий пример. Фирма производит шесть типов стульев: капитан, помощник, маркиза, испанский, венский и офисный. Для производства стульев необходимы универсальные детали: длинные и короткие болты, тяжелые и легкие сиденья, длинные и короткие ножки, перекладины, гайки, роллеры, каркас и крепления. В табл. 1 приводятся данные о стоимости стульев, потребности в деталях для каждого типа стульев и их наличие на складе.
Благодаря универсальности деталей производитель может быстро реагировать на изменения в спросе. Поступил заказ изготовить 40 стульев каждого типа из имеющихся на складе деталей.
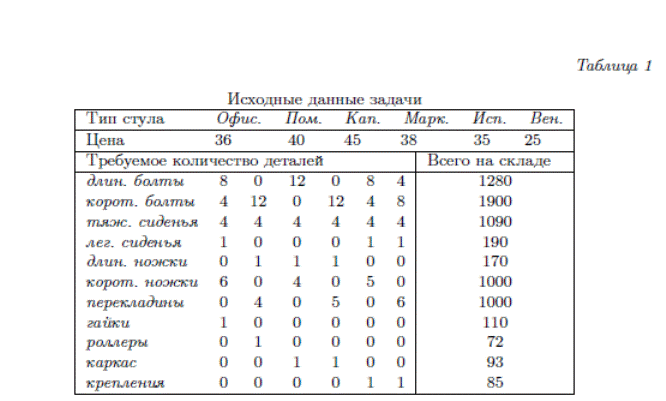
Суммарный доход от продажи стульев определяется выражением:
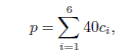
где i — тип стула, ci — стоимость одного стула i-го типа. Результаты расче-
тов для склада приводятся в табл. 2. Согласно этому плану доход составляет
8760 y.e., причем длинные болты израсходованы полностью. Можно ли уве-
личить доход фирмы, если количество стульев в заказе будет другим? Чтобы
ответить на этот вопрос, проанализируем решение. Заметим, что для стула
≪капитан≫ длинных болтов требуется больше, чем для других стульев.
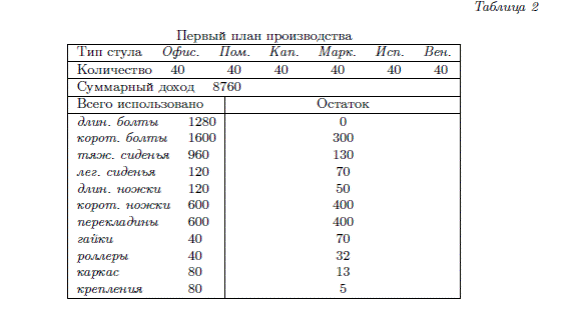
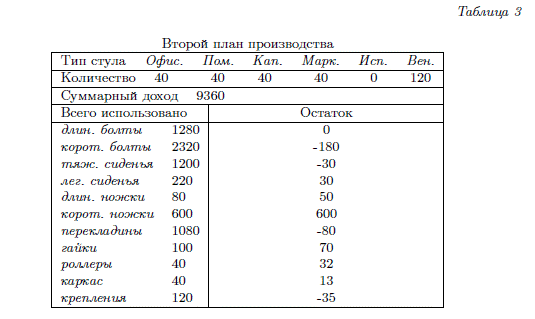
Сократим производство стульев ≪капитан≫ на 2 единицы, а на вырученные 24 длинных болта произведем 3 ≪офисных≫ стула. При этом фирма потеряет от не производства ≪капитана≫ 90 y.e., но заработает 108 y.e., если продаст дополнительно три ≪офисных≫ стула. Таким образом, суммарный доход увеличится на 18 = (43 · 36 + 40 · 40 + 38 · 45 + 40 · 38 + 40 · 35 + 40 · 25 − 8760) y.e. Можно ли еще увеличить доход? Проведем те же рассуждения. Для производства ≪испанского≫ стула необходимо 8 длинных болтов, а для ≪венского≫ в 2 раза меньше. Значит, если вместо одного ≪испанского≫ стула будем производить два ≪венских≫ стула, то доход составит не 35 y.e., а 50 y.e. Следовательно, если фирма будет производить вместо 40 ≪испанских≫ стульев 80 ≪венских≫ стульев, то ее суммарный доход увеличится на 600 = (40 · 36 + 40 · 40 + 40 ·
45 + 40 · 38 + 0 · 35 + 120 · 25− 8760) y.e. Результаты расчетов по этому плану
приводятся в табл. 3. Однако этот план не может быть реализован из-за недостатка деталей на складе, о чем свидетельствуют отрицательные значения в столбце остаток.
В этой задаче мы использовали количественную модель, отражающую взаимосвязь между количеством производимых стульев, количеством деталей и суммарным доходом. Однако если фирме нужно ответить на вопрос о том, сколько произвести стульев, чтобы получить максимальный доход, то количественная модель в этом не поможет, и нужно сформулировать модель принятия решений. Далее будут описаны способы построения различных моделей принятия решений, разобрано, насколько хорошей является сформулированная математическая модель и как ее улучшить.
Модели принятия решений, в которых ищется максимум (минимум) некоторой функции от переменных принятия решений при некоторых ограничениях
называют также оптимизационными моделями. Под ограничениями понимают условия, которые препятствуют получению максимального (минимального) значения целевой функции, т. е. не дают, например, сократить затраты до 0 или достигнуть бесконечно большого дохода. В задаче про стулья в качестве ограничений были условия на наличие деталей на складе. В других задачах ограничения могут возникать в результате ограниченного бюджета, ограниченного времени выполнения проекта, ограниченных производственных мощностей, вместимости складов, а также из-за различных требований к производственному процессу, допустимым объемам затрат и др.
Оптимизационные модели активно стали использоваться в годы Второй ми-
ровой войны при решении военных задач. Со временем сложились научные
дисциплины исследование операций (от англ. operations research) и теория принятия решений (от англ. management science), которые занимаются оптимизационными задачами, возникающими в экономике, производстве, политике и других областях человеческой деятельности. Под исследованием операций понимают применение математических и количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности.
Практическая работа №4
Тема: Решение задач по теме: «Точные и приблизительные вычисления».
Цель урока:
· Изучить свойства систем управления, статические характеристики звеньев системы;
· Развивать умения применять формулируемые знания в новых ситуациях;
· Воспитывать самоанализ в новых ситуациях.
Оборудование:
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
· Правила составления электрических схем;
· Закон Ома, законы Кирхгофа;
· Условно-графические обозначения.
Студент должен уметь:
· Определять токи в ветвях электрической цепи;
· Определять входное сопротивление;
· Находить неизвестные токи и напряжение на зажимах источника ЭДС в электрической цепи.
Вопросы для повторения
1. Как определить входное сопротивление, если элементы соединены последовательно?
2. Как определить входное сопротивление, если элементы соединены параллельно?
3. Как определить входное сопротивление, если элементы соединены путём последовательных преобразований?
4. Чему равны согласно принципу наложения действительные токи в ветвях электрической цепи?
Ход работы:
В практике вычислений приходиться выполнять главным образом приближенные вычисления. При решении той или иной задачи иногда можно получить точный числовой ответ, но найти его довольно сложно, а на практике точное значение искомой величины часто бывает не нужно, зачастую высокая точность ответа не имеет никакого практического смысла. Бывает и иначе: найти точный ответ вообще невозможно. Поясним сказанное примерами.
Пример 1. Пассажир живет на расстоянии 1320м от платформы вокзала. За сколько времени до отхода поезда пассажир должен выйти из дому при скорости 5км/ч?
Можно получить точное решение задачи: пассажир должен выйти из дому за 15 мин 50,4 сек! Однако вряд ли в действительности кто-либо стал бы пользоваться этим точным математическим решением, и вот почему. Вычисления выполнены совершенно точно, но точно ли измерено расстояние до платформы? Да и можно ли вообще измерить путь пешехода, не допустив никаких погрешностей? А скорость 5 км/ч - разве она определена абсолютно точно?
Вполне понятно, что каждый отдаст предпочтение не «математически точному», а «практическому» решению этой задачи, т.е. прикинет, что надо идти 15-20 минут, и прибавит еще несколько минут для гарантии.
Для чего же в таком случае вычислять секунды и их десятые доли и стремиться к той степени точности, которой нельзя воспользоваться на практике?
Пример 2. Требуется вычислять объем параллелепипеда, длины ребер которого равны а =3,42 м, b = 4,37 м, c = 3,27 м ( предполагается, что все эти числа - точные). Применяя формулу объема параллелепипеда V=a·b·c, можно получить точное значение объема: 48,871458 м3 . Мы получили многозначное число, неудобное для практического использования. Нужна ли такая точность? В известных условиях может быть и нужна. Если производится физический эксперимент, изучается некоторое явление в камере, имеющей форму параллелепипеда, и требуется точно вычислить объем, то полученный ответ мы и используем без всяких изменений.
Но пусть наш параллелепипед - это комната, объем которой требуется определить. При этом a, b, c (ширина, длина, высота) найдены путем измерения обыкновенной линейкой, так что при измерении длины возможна погрешность до 1см. Погрешность сомножителей оказывает влияние на полученный результат. Теория приближенных вычислений показывает, что погрешность результата умножения может достичь 0.4 м3. Ясно, что в полученном ответе все цифры справа от запятой не имеют никакого смысла. Округляя, получаем приближенный ответ: V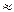 
49 м3. Более точного результата мы добиться не можем, так как исходные данные a, b, c лишь приближенные значения длины, ширины, высоты. К тому в данных условиях знать объем с большей точностью вовсе и не требуется .
Существуют три источника получения чисел: счет, измерения и выполнение различных математических операций.
В результате счета мы получаем целое положительное число. Это число принципиально всегда является точным. Однако на практике часто бывает трудно произвести операцию счета, и тогда число оказывается приближенным. Например, было подсчитано, что население некоторого города к 1 января 1974г. составляло 143 278 человек. Мы не уверены, что это число точно, так как полный учет всех жителей осуществить трудно: люди непрерывно уезжают и приезжают, рождаются и умирают.
В результате измерения всегда получается приближенное значение величины. Любое измерение нельзя выполнить абсолютно точно. При выполнении измерения тем или иным прибором неизбежна некоторая погрешность («ошибка прибора», «ошибка измерения»).
Практическая работа №5
Тема: Решение задач по теме: « Абсолютная и относительная погрешность»
Цель урока:
· Освоить методы исследования случайных процессов;
· Развивать умения применять формулируемые знания в новых ситуациях;
· Воспитывать самоанализ в новых ситуациях.
Оборудование:
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
· Графический интерфейс MS Excel;
· Правила построения графиков;
· Характеристики случайных процессов.
Студент должен уметь:
· Создавать графики, диаграммы и гистограммы случайных процессов;
· Рассчитывать характеристики случайных процессов.
Вопросы для повторения
1. Чем отличается процесс с непрерывным состоянием от процесса с дискретным состоянием?
2. Какой случайный процесс называется процессом с дискретным временем?
3. Что такое случайный процесс?
Ход работы:
Физические величины характеризуются понятием «точность погрешности». Есть высказывание, что путем проведения измерений можно прийти к познанию. Так удастся узнать, какова высота дома или длина улицы, как и многие другие. Введение Разберемся в значении понятия «измерить величину». Процесс измерения заключается в том, чтобы сравнить её с однородными величинами, которые принимают в качестве единицы. Для определения объёма используются литры, для вычисления массы применяются граммы. Чтобы было удобнее производить расчеты, ввели систему СИ международной классификации единиц. За измерение длины вязли метры, массы – килограммы, объёма – кубические литры, времени – секунды, скорости – метры за секунду. При вычислении физических величин не всегда нужно пользоваться традиционным способом, достаточно применить вычисление при помощи формулы. К примеру, для вычисления таких показателей, как средняя скорость, необходимо поделить пройденное расстояние на время, проведенное в пути. Так производятся вычисления средней скорости. Применяя единицы измерения, которые в десять, сто, тысячу раз превышают показатели принятых измерительных единиц, их называют кратными. Наименование каждой приставки соответствует своему числу множителя: Дека. Гекто. Кило. Мега. Гига. Тера. В физической науке для записи таких множителей используется степень числа 10. К примеру, миллион обозначается как 106. В простой линейке длина имеет единицу измерения – сантиметр. Она в 100 раз меньше метра. 15-сантиметровая линейка имеет длину 0,15 м. Линейка является простейшим видом измерительных приборов для того, чтобы измерять показатели длины. Более сложные приборы представлены термометром – чтобы измерять температуру, гигрометром – чтобы определять влажность, амперметром – замерять уровень силы, с которой распространяется электрический ток. Насколько точны будут показатели проведенных измерений?
Возьмем линейку и простой карандаш. Наша задача заключается в измерении длины этой канцелярской принадлежности. Для начала потребуется определить, какова цена деления, указанная на шкале измерительного прибора. На двух делениях, которые являются ближайшими штрихами шкалы, написаны цифры, к примеру, «1» и «2». Необходимо подсчитать, сколько делений заключено в промежутке этих цифр. При правильном подсчете получится «10». Вычтем от того числа, которое является большим, число, которое будет меньшим, и поделим на число, которое составляют деления между цифрами: (2-1)/10 = 0,1 (см) Так определяем, что ценой, определяющей деление канцелярской принадлежности, является число 0,1 см или 1 мм. Наглядно показано, как определяется показатель цены для деления с применением любого измерительного прибора. Измеряя карандаш с длиной, которая немного меньше, чем 10 см, воспользуемся полученными знаниями. При отсутствии на линейке мелкого деления, следовал бы вывод, что предмет имеет длину 10 см. Это приблизительное значение названо измерительной погрешностью. Она указывает на тот уровень неточности, которая может допускаться при проведении измерений. Определяя параметры длины карандаша с более высоким уровнем точности, большей ценой деления достигается большая измерительная точность, которая обеспечивает меньшую погрешность. При этом абсолютно точного выполнения измерений не может быть. А показатели не должны превышать размеры цены деления. Установлено, что размеры измерительной погрешности составляют ½ цены, которая указана на делениях прибора, который применяется для определения размеров. После выполнения замеров карандаша в 9,7 см определим показатели его погрешности. Это промежуток 9,65 - 9,85 см. Формулой, измеряющей такую погрешность, является вычисление:
А = а ± D (а)
А - в виде величины для измерительных процессов;
а - значение результата замеров;
D - обозначение абсолютной погрешности.
Если слаживать или вычитать величины с учетом погрешности, это число будет составлять сумму цифр, которые и обозначают погрешность, и имеются у каждой отдельно взятой величины. При вычитании или складывании величин с погрешностью результат будет равен сумме показателей погрешности, которую составляет каждая отдельная величина. Знакомство с понятием Если рассматривать классификацию погрешностей в зависимости от способа её выражения, можно выделить такие разновидности:
Абсолютную.
Относительную.
Приведенную.
Абсолютная погрешность измерений обозначается буквой «Дельта» прописной. Это понятие определяется в виде разности между измеренными и действительными значениями той физической величины, которая измеряется. Выражением абсолютной погрешность измерений являются единицы той величины, которую необходимо измерить. При измерении массы она будет выражаться, к примеру, в килограммах. Это не эталон точности измерений. Как рассчитать погрешность прямых измерений? Есть способы изображения погрешности измерения и их вычисления. Для этого важно уметь определять физическую величину с необходимой точностью, знать, что такое абсолютная погрешность измерений, что её никто никогда не сможет найти. Можно вычислить только её граничное значение. Даже если условно употребляется этот термин, он указывает именно на граничные данные. Абсолютная и относительная погрешность измерений обозначаются одинаковыми буквами, разница в их написании. При измерении длины абсолютная погрешность будет измеряться в тех единицах, в которых исчисляться длина. А относительная погрешность вычисляется без размеров, так как она является отношением абсолютной погрешности к результату измерения. Такую величину часто выражают в процентах или в долях. Абсолютная и относительная погрешность измерений имеют несколько разных способов вычисления в зависимости от того, какой метод измерения физических величин. Понятие прямого измерения Абсолютная и относительная погрешность прямых измерений зависят от класса точности прибора и умения определять погрешность взвешивания. Прежде чем говорить о том, как вычисляется погрешность, необходимо уточнить определения. Прямым называется измерение, при котором происходит непосредственное считывание результата с приборной шкалы. Когда мы пользуемся термометром, линейкой, вольтметром или амперметром, то всегда проводим именно прямые измерения, так как применяем непосредственно прибор со шкалой.
Есть два фактора, которые влияют на результативность показаний: Погрешностью приборов.
Погрешностью системы отсчета.
Граница абсолютной погрешности при прямых измерениях будет равна сумме погрешности, которую показывает прибор, и погрешности, которая происходит в процессе отсчета. D = D (пр.) + D (отс.)
Пример с медицинским термометром Показатели погрешности указаны на самом приборе. На медицинском термометре прописана погрешность 0,1 градусов Цельсия. Погрешность отсчета составляет половину цены деления.
D отс. = С/2 Если цена деления 0,1 градуса, то для медицинского термометра можно произвести вычисления: D = 0,1o С + 0,1o С / 2 = 0,15o С На тыльной стороне шкалы другого термометра есть ТУ и указано, что для правильности измерений необходимо погружать термометр всей тыльной частью. Точность измерения не указана. Остается только погрешность отсчета. Если цена деления шкалы этого термометра равна 2o С, то можно измерять температуру с точностью до 1o С. Таковы пределы допускаемой абсолютной погрешности измерений и вычисление абсолютной погрешности измерений. Особую систему вычисления точности используют в электроизмерительных приборах. Точность электроизмерительных приборов Чтобы задать точность таких устройств, используется величина, называемая классом точности. Для её обозначения применяют букву «Гамма». Чтобы точно произвести определение абсолютной и относительной погрешности измерений, нужно знать класс точности прибора, который указан на шкале. Возьмем, к примеру, амперметр. На его шкале указан класс точности, который показывает число 0,5. Он пригоден для измерений на постоянном и переменном токе, относится к устройствам электромагнитной системы. Это достаточно точный прибор. Если сравнить его со школьным вольтметром, видно, что у него класс точности – 4. Эту величину обязательно знать для дальнейших вычислений. Применение знаний Таким образом, D c = c (max) Х γ /100 Этой формулой и будем пользоваться для конкретных примеров. Воспользуемся вольтметром и найдем погрешность измерения напряжения, которое дает батарейка.
Подключим батарейку непосредственно к вольтметру, предварительно проверив, стоит ли стрелка на нуле. При подключении прибора стрелка отклонилась на 4,2 деления. Это состояние можно охарактеризовать так: Видно, что максимальное значение U для данного предмета равно 6. Класс точности –(γ) = 4. U(о) = 4,2 В. С=0,2 В Пользуясь этими данными формулы, абсолютная и относительная погрешность измерений вычисляется так: D U = DU (пр.)+ С/2 D U (пр.) = U (max) Х γ /100 D U (пр.) = 6 В Х 4/100 = 0, 24 В Это погрешность прибора. Расчет абсолютной погрешности измерений в этом случае будет выполнен так: D U = 0,24 В + 0,1 В = 0,34 В По рассмотренной формуле без труда можно узнать, как рассчитать абсолютную погрешность измерений. Существует правило округления погрешностей. Оно позволяет найти средний показатель между границей абсолютной погрешности и относительной. Учимся определять погрешность взвешивания Это один из примеров прямых измерений. На особом месте стоит взвешивание. Ведь у рычажных весов нет шкалы. Научимся определять погрешность такого процесса. На точность измерения массы влияет точность гирь и совершенство самих весов. Мы пользуемся рычажными весами с набором гирь, которые необходимо класть именно на правую чашу весов. Для взвешивания возьмем линейку. Перед началом опыта нужно уравновесить весы. Линейку кладем на левую чашу. Масса будет равна сумме установленных гирь. Определим погрешность измерения этой величины.
D m = D m (весов) + D m (гирь) Погрешность измерения массы складывается из двух слагаемых, связанных с весами и гирями. Чтобы узнать каждую из этих величин, на заводах по выпуску весов и гирь продукция снабжается специальными документами, которые позволяют вычислить точность. Применение таблиц Воспользуемся стандартной таблицей. Погрешность весов зависит от того, какую массу положили на весы. Чем она больше, тем, соответственно, больше и погрешность. Даже если положить очень легкое тело, погрешность будет. Этот связано с процессом трения, происходящим в осях. Вторая таблица относится к набору гирь. На ней указано, что каждая из них имеет свою погрешность массы. 10-граммовая имеет погрешность в 1 мг, как и 20-граммовая. Просчитаем сумму погрешностей каждой из этих гирек, взятой из таблицы. Удобно писать массу и погрешность массы в двух строчках, которые расположены одна под другой. Чем меньше гири, тем точнее измерение.
Итоги В ходе рассмотренного материала установлено, что определить абсолютную погрешность невозможно. Можно лишь установить её граничные показатели. Для этого используются формулы, описанные выше в вычислениях.
Практическая работа №6
Тема: Решение систем линейных и нелинейных уравнений.
Цель урока:
· Научиться выполнять чертежи структурных схем в системе AutoCAD;
· Развивать умения применять формулируемые знания в новых ситуациях;
· Воспитывать самоанализ в новых ситуациях.
Оборудование:
· Компьютеры;
· Программа AutoCAD;
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
· Графический интерфейс системы AutoCAD;
· Порядок создания чертежа.
Студент должен уметь:
· Использовать команды для создания и редактирования графических примитивов;
· Создавать блоки и блоки с атрибутами для УГО;
· Вставлять блоки в чертёж.
Вопросы для повторения
1. Что называют графическим примитивом?
2. Какие команды AutoCAD относятся к командам для создания графических примитивов?
3. Какие команды AutoCAD относятся к командам для редактирования графических примитивов?
4. Что такое блок и какие он имеет атрибуты?
5. Как вставить точку в чертёж?
6. Как вставить текст в чертёж?
Ход работы:
Дата: 2019-12-10, просмотров: 570.
