В отличие от систем линейных уравнений для систем нелинейных уравнений не известны прямые методы решения. Лишь в отдельных случаях систему можно решить непосредственно. Например, для системы из двух уравнений иногда удается выразить одно неизвестное через другое и таким образом свести задачу к решению одного нелинейного уравнения относительно одного неизвестного. Поэтому итерационные методы для нелинейных систем приобретают особую актуальность.
Метод Ньютона.
Рассмотрим нелинейную систему уравнений
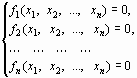
| (23) |
или в векторной форме
| f (x) = 0, | (23 ') |
где
f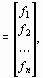 
x 
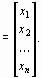
Для решения системы (23? ) будем пользоваться методом последовательных приближений.
Предположим, известно k-е приближение
x(k) =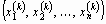 
одного из изолированных корней x =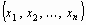 
векторного уравнения (23 '). Тогда точный корень уравнения (23') можно представить в виде
| х= x(k) + D x(k), | (24) |
где D x(k) =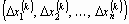 
- поправка (погрешность корня).
Подставляя выражение (24) в (23'), будем иметь
| f (x(k) + D x(k)) = 0. | (25) |
Предполагая, что функция f (x) непрерывно дифференцируема в некоторой выпуклой области, содержащей x и x(k), разложим левую часть уравнения (25) по степеням малого вектора D x(k) , ограничиваясь линейными членами,
| f (x(k) + D x(k)) = f (x(k)) + f ? (x(k)) D x(k) = 0 | (26) |
или, в развернутом виде,
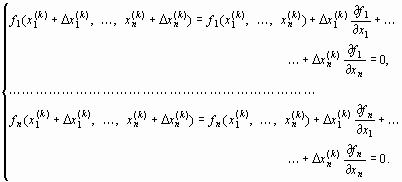
| (26') |
Из формул (26) и (26') вытекает, что под производной f '(x) следует понимать матрицу Якоби системы функций f1, f2, ..., fn относительно переменных x1, x2, ..., xn, т. е.
f ' (x) = W(x) =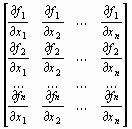 
,
или в краткой записи
f ' (x) = W(x) =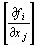 
(i, j = 1, 2, …, n).
Поэтому формула (26) может быть записана в следующем виде:
f (x(k) ) + W (x(k) ) D x(k) = 0
Если det W ( х ) =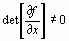 
, то D x(k) = - W -1(x(k)) f (x(k)).
Отсюда видно, что метод Ньютона решения системы (23) состоит в построении итерационной последовательности:
| x(k + 1) = x(k) - W -1(x(k)) f (x(k)) (k = 0, 1, 2, …). | (27) |
Если все поправки становятся достаточно малыми, счет прекращается. Иначе новые значения xi используются как приближенные значения корней, и процесс повторяется до тех пор, пока не будет найдено решение или не станет ясно, что получить его не удастся.
Пример 9. Методом Ньютона приближенно найти положительное решение системы уравнений
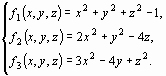
исходя из начального приближения x0 = y0 = z0 =0,5.
Полагая:
х(0) =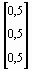 
, f (х) = 
,
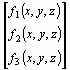имеем:
f (х) =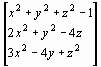 
Отсюда
f ( х(0) ) =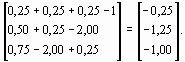 
Составим матрицу Якоби
W(x) =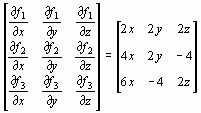 
Имеем
W ( х(0) ) =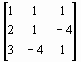 
, причем D = det W ( х(0) ) =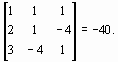 
Следовательно, матрица W ( х(0) ) - неособенная. Составим обратную ей матрицу
W -1 ( х(0) ) =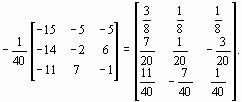 
По формуле (27) получаем первое приближение
х(1) = x(0) - W -1(x(0) ) f (x(0) ) =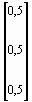 
- 
= 
+ 
= 
.
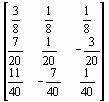
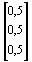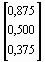Аналогично находятся дальнейшие приближения. Результаты вычислений приведены в Таблице 3.
Таблица 3
Последовательные приближения корней
| i | x | y | z |
| 0 | 0,5 | 0,5 | 0,5 |
| 1 | 0,875 | 0,5 | 0,375 |
| 2 | 0,78981 | 0,49662 | 0,36993 |
| 3 | 0,78521 | 0,49662 | 0,36992 |
Останавливаясь на приближении x(3) , будем иметь:
x = 0,7852; y = 0,4966; z =0,3699.
Практическая работа №7
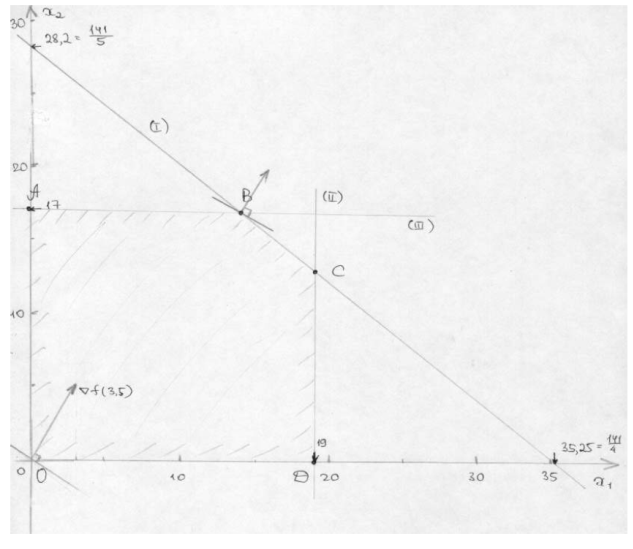
Тема: Задачи линейного программирования (ЗЛП)
Цель урока:
· Научиться устанавливать режимы рисования, объектную привязку;
· Научиться корректировать чертежи командами редактирования;
· Изучить команды ПОДОБИЕ и КОПИРОВАТЬ;
· Развивать умения применять формулируемые знания в новых ситуациях;
· Воспитывать самоанализ в новых ситуациях.
Оборудование:
· Компьютеры;
· Программа AutoCAD;
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
· Команды для установки режимов рисования;
· Команды редактирования;
· Что такое вспомогательные построения.
Студент должен уметь:
· Устанавливать режимы рисования;
· Пользоваться различными способами ввода координат точек;
· Корректировать чертежи командами редактирования.
Вопросы для повторения
1. Какая команда задаёт области чертежа?
2. Что задают клавиши F7, F8, F9?
3. Что такое объектная привязка?
4. Что выполняет команда Массив?
Ход работы:
Практическая работа №8
Тема: Транспортная задача
Цель урока:
· изучить понятие транспортной задачи;
· развить навыки решения транспортных задач при помощи метода потенциалов;
· Развивать умения применять формулируемые знания в новых ситуациях;
· Воспитывать самоанализ в новых ситуациях.
Оборудование:
· Компьютеры;
· Программа AutoCAD;
· Мультимедийный проектор;
· Раздаточный материал.
Студент должен знать:
- понятие транспортной задачи;
- методы решения транспортной задачи.
Студент должен уметь:
- применять различные методы для решения транспортной задачи.
Вопросы для повторения
1. Что такое транспортная задача?
2. Какой план перевозок называется допустимым?
3. Какие существуют методы решения транспортной задачи?
4. Как построить опорный план для транспортной задачи?
Ход работы:
Структурная схема терминов
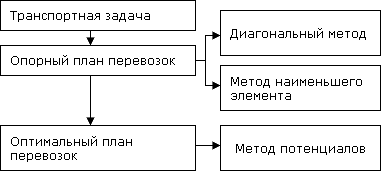
Построение математической модели транспортной задачи
Мы рассмотрели общие подходы к решению задач линейного программирования. Однако существуют частные типы задач линейного программирования, которые в силу своей структуры допускают решения более простыми методами. Мы остановимся только на одной из них – так называемой транспортной задаче.
Пример 1
Фирма должна отправить некоторое количество кроватей с трёх складов в пять магазинов. На складах имеется соответственно 15, 25 и 20 кроватей, а для пяти магазинов требуется соответственно 20, 12, 5, 8 и 15 кроватей. Стоимость перевозки одной кровати со склада в магазин приведены в таблице.
Склады
Магазины
Как следует спланировать перевозку, чтобы её стоимость была минимальной?
Дата: 2019-12-10, просмотров: 260.
