Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Электрическая цепь, или, короче, цепь постоянного тока в общем случае содержит источники и приёмники электрической энергии, измерительные приборы, коммутационную аппаратуру и соединительные линии и провода.

В источниках электрической энергии осуществляется преобразование в электрическую энергию каких-либо других форм энергии, например энергии химических процессов в гальванических элементах и аккумуляторах, тепловой энергии в термопреобразователях на основе термопар.

В приемниках электрической энергии электрическая энергия преобразуется, например, в механическую (двигатели постоянного тока), тепловую (электрические печи), химическую (электролизные ванны).

Коммутационная аппаратура, линии и измерительные приборы служат для передачи электрической энергии от источников, распределения ее между приемниками и контроля режима работы всех электротехнических устройств.

Графическое изображение электрической цепи называют схемой. В лабораторных работах электрические цепи собирают по принципиальным схемам, в которых каждое электротехническое устройство заменено (по правилам ГОСТ) его условным обозначением. Принципиальная схема показывает назначение электротехнических устройств и их взаимодействие (рис. 1.1, а).

 

 

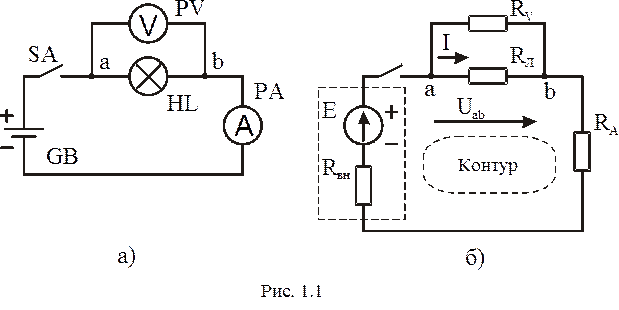
При замыкании ключа SA к лампе накаливания HL – приемнику электрической энергии – подключается источник электрической энергии постоянного тока – аккумуляторная батарея GB. Для контроля режима приемника энергии включены амперметр РА и вольтметр PV.

Но принципиальная схема неудобна при расчетах режима работы цепи. Поэтому чтобы выполнить расчет, необходимо каждое из электротехнических устройств представить его схемой замещения. Схема замещения электрической цепи состоит из совокупности различных идеализированных элементов, выбранных так, чтобы можно было с заданным или необходимым приближением описать процессы в цепи.

Конфигурация схемы замещения цепи определяется понятиями: ветвь, узел, контур. Ветвь схемы состоит из одного или нескольких последовательно соединенных элементов, каждый из которых имеет два вывода (начало и конец),причем к концу каждого предыдущего элемента присоединяется начало следующего. В узле схемы соединяются три или большее число ветвей. Контур – замкнутый путь, проходящий по нескольким ветвям так, что ни одна ветвь и ни один узел не встречаются больше одного раза.

Схема замещения рис. 1.1,б цепи, показанной на рис. 1.1,а, содержит три ветви, причем две состоят из одного элемента каждая (R_Л и R_V), а третья – из трех элементов (Е, R_ВН и R_А). На рис. 1.1,б указаны параметры элементов: R_Л – сопротивление лампы накаливания, R_V – сопротивление вольтметра, R_А – сопротивление амперметра, Е – электродвижущая сила (ЭДС) аккумуляторной батареи и R_ВН – ее внутреннее сопротивление. Три ветви соединены в двух узлах a и b.

Если значения параметров всех элементов схемы замещения цепи известны, то , пользуясь законами электротехники, можно рассчитать режим работы всех ее элементов, т. е. определить электрическое состояние всех электротехнических устройств.

Далее в тексте вместо термина схема замещения электрической цепи будем пользоваться сокращенными терминами схема цепи или, еще короче, схема.

При замыкании ключа SA в цепи (рис. 1.1,а) во всех токопроводящих частях электротехнических устройств, т.е. во всех элементах схемы замещения рис. 1.1,б, будет постоянный ток.

Согласно электронной теории электропроводности, валентные электроны в металлах легко отделяются от атомов, которые становятся положительными ионами. Ионы образуют в твердом теле кристаллическую решетку с пространственной периодичностью. Свободные электроны хаотически движутся в пространстве решетки между атомами (тепловое движение), сталкиваясь с ними.

Под действием продольного электрического поля, создаваемого в проводнике источником электрической энергии, свободные электроны приобретают скорость (дрейфовую скорость) и дополнительно перемещаются в одном направлении – вдоль проводника. Таким образом, постоянный ток в проводящей среде представляет собой упорядоченное движение положительных и отрицательных зарядов под действием электрического поля. Принято считать направлением тока I направление положительных зарядов, т.е. направление, обратное направлению движения электронов в проводнике под действием электрического поля. Это направление выбирается произвольно и указывается стрелкой (рис. 1.1,б). Постоянный ток в цепи измеряется амперметром, например, магнитоэлектрической или электродинамической систем, а также электронным амперметром.

Единицей тока в международной системе единиц (СИ) является ампер (А). Примем в расчетах схем сопротивление амперметра R_А = 0.

Под напряжением U на некотором элементе схемы понимают разность потенциалов на его концах. Положительное направление напряжения на элементе схемы как и положительное направление тока может быть выбрано произвольно и указывается стрелкой, но для участка цепи, не содержащего источника энергии рекомендуется выбирать его совпадающим с положительным направлением тока. Так на рис. 1.1,б выводы лампы накаливания обозначены а и b. Чтобы указать положительное направление напряжения на лампе необходимо стрелку направить от вывода а к выводу b и записать U = U_ab. Здесь направления тока и напряжения совпадают.

Единицей напряжения в системе СИ является вольт (В).

Для измерения напряжения на участках или элементах цепи постоянного тока применяются вольтметры, например, магнитоэлектрической и электродинамической систем, а также электронные вольтметры. Примем в расчетах схем сопротивление вольтметра R_V равное бесконечности.

Столкновения свободных электронов в проводниках с атомами кристаллической решетки тормозят их поступательное движение. Это противодействие направленному движению свободных электронов, т.е. постоянному току, составляет физическую сущность сопротивления проводника. Аналогичен механизм сопротивления постоянному току в электролитах и газах. При этом термин сопротивление и соответствующее ему буквенное обозначение R применяются как для обозначения самого элемента цепи, так и количественной оценки его величины.

Величина, обратная сопротивлению, называется проводимостью: g = 1/ R.

Единицей сопротивления в системе СИ является ом (Ом), а проводимости – сименс (См).

Проводящие свойства материала определяют его объемное удельное сопротивление ρ _V, равное сопротивлению между противоположными сторонами куба с ребром 1м, изготовленного из данного материала. Величина обратная объемному удельному сопротивлению, называется объемной удельной проводимостью: γ _V =1/ ρ_V.

Единицей объемного сопротивления является 1Ом · м, а объемной удельной проводимости – 1 См · м.

Сопротивление проводника постоянному току зависит от температуры. В общем случае наблюдается достаточно сложная зависимость. Но при изменениях температуры в относительно узких пределах (примерно 200ºС) ее можно выразить формулой

R₂=R₁[1+α(θ₂-θ₁)],

где R₂ и R₁ – сопротивления соответственно при температурах θ₂ и θ₁; α – температурный коэффициент сопротивления, равный относительному изменению сопротивления при изменении температуры на 1ºС.

В табл. 1.1 приведены значения объемного удельного сопротивления ρ_V и температурного коэффициента сопротивления α для некоторых токопроводящих материалов, где 1 мк Ом = 10^{– 6} Ом.

Таблица 1.1

Материал	Объемное удельное сопротивление при 20ºС, мк Ом ·м	Температурный коэффициент сопротивления (на 1ºС)
Серебро	0,016	0,0035
Медь	0,0172…0,0182	0,0041
Алюминий	0,0295	0,004
Сталь	0,125…0,146	0,0057
Железо	0,09…0,11	0,006
Свинец	0,218…0,222	0,0039
Вольфрам	0,0503	0,0048
Уголь	10…60	0,005
Константан	0,44	0,00005

Также сопротивление участка однородного проводника постоянному току зависит от длины проводника 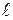 (м) и площади его поперечного сечения S (м²):

.

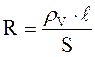Электротехническое устройство, обладающее сопротивлением и применяемое для ограничения тока, называется резистором. Регулируемый резистор называется реостатом.

Резистивными элементами называются идеализированные модели резисторов и любых других электротехнических устройств или их частей, оказывающих сопротивление постоянному току независимо от физической природы этого явления. Они применяются при составлении схем замещения цепей и расчетах их режимов. При идеализации пренебрегают токами через изолирующие покрытия резисторов, каркасы проволочных реостатов и т.п. На схемах замещения резисторы имеют условные графические изображения:

 

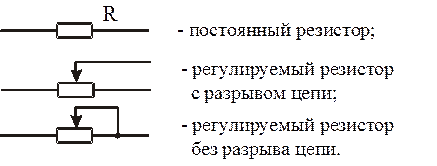
Линейный резистивный элемент является схемой замещения любой части электротехнического устройства, в которой ток пропорционален напряжению. Его параметром служит сопротивление R = const. Вольтамперная характеристика (ВАХ) линейного резистивного элемента и его условное обозначение на схемах замещения приведены на рис. 1.2, а. Электрическая цепь постоянного тока с такими элементами называется линейной.

Если на участке цепи зависимость тока от напряжения нелинейна, то схема замещения этого участка содержит нелинейный резистивный элемент, который задается нелинейной ВАХ I (U) (рис. 1.2, б). К нелинейным резистивным элементам относятся лампы накаливания, терморезисторы, полупроводниковые диоды и триоды, электронные лампы и т.д. Электрические цепи постоянного тока с нелинейными резистивными элементами называются нелинейными.

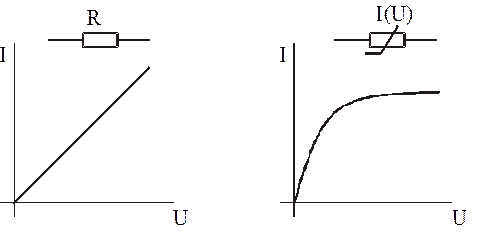
         а)                                                           б)

Рис. 1.2

В цепи постоянного тока источниками электрической энергии являются источник электродвижущей силы (ЭДС) и источник тока. Источником ЭДС может служить, например, гальванический элемент, в котором между электродами создана разность потенциалов сторонними силами (в данном случае химической природы). Количественную меру сторонней силы принято называть электродвижущей силой Е. Направленное движение положительных зарядов внутри источника под действием сторонних сил сопровождается их взаимными столкновениями, что создает внутреннее сопротивление R_ВН гальванического элемента постоянному току.

Гальванический элемент, как источник энергии, можно представить схемой замещения, которая показана пунктиром на рис. 1.3,а. Она состоит из последовательно включенных источника ЭДС Е и резистивного элемента с сопротивлением R _ВН, равным его внутреннему сопротивлению. Стрелка ЭДС указывает направление движения положительных зарядов внутри источника под действием сторонних сил. Если к выводам источника а и b подключить резистор с сопротивлением нагрузки R_H, то по замкнутой цепи потечет ток I (рис. 1.3,а). Свойства источника энергии определяет ВАХ – зависимость напряжения между его выводами U = U_ab   от  тока I   источника, т.е. U(I):

U = Е - I·R_ВН, которой соответствует прямая 1 на рис. 1.3,в. Источник электрической энергии с малым внутренним сопротивлением можно заменить идеализированной моделью, для которой R_ВН = 0. Такой идеализированный источник называется идеальным источником ЭДС с одним параметром

Е = U.

 

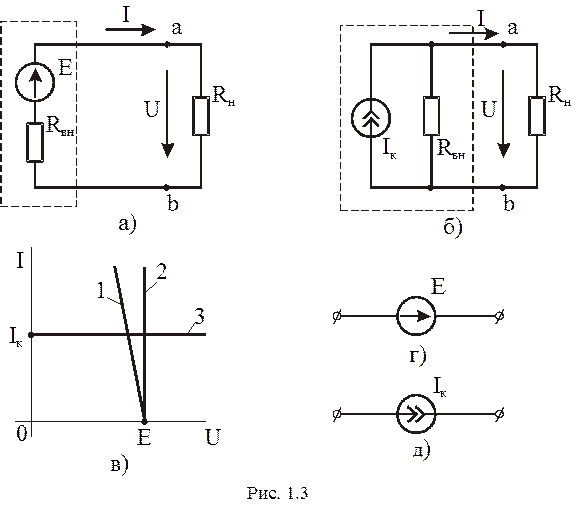
Напряжение между выводами идеального источника ЭДС не зависит от тока, а его ВАХ определяется выражением U = Е = const, которому соответствует прямая 2 на рис. 1.3,в. Такой источник называется также источником напряжения.  Изображение  идеального  источника  ЭДС на схемах показано на рис. 1.3,г.

В дальнейшем в схемах замещения используется идеальный источник ЭДС.

В ряде специальных случаев, в частности в цепях с полупроводниковыми приборами и электронными лампами, внутреннее сопротивление R_ВН источника электрической энергии может быть во много раз больше сопротивления нагрузки R_Н (внешней по отношению к источнику части цепи). Схема замещения такого источника показана пунктиром на рис. 1.3,б. Источник энергии I _К и его внутреннее сопротивление R_ВН соединены между собой параллельно. Ток, протекающий по сопротивлению нагрузки R_Н (рис. 1.3,б), вычисляется по формуле I = I _К R _ВН / ( R _ВН + R_Н).

Источник электрической энергии с большим внутренним сопротивлением можно заменить идеализированной моделью, для которой R _ВН → ∞. Такой идеализированный источник называется идеальным источником тока с одним параметром I = I _К. Ток источника тока не зависит от напряжения U = U_ab между его выводами, а его ВАХ определяется выражением I = I _К = const, которому соответствует прямая 3 на рис. 1.3,в. Изображение идеального источника тока на схемах показано на рис. 1.3, д.

В дальнейшем в схемах замещения используется идеальный источник тока.

Следует отметить, что представление реальных источников электрической энергии в виде двух схем замещения (рис. 1.3,а) и (рис. 1.3,б) является эквивалентным представлением относительно внешнего участка цепи: в обоих случаях одинаковы напряжения между выводами а и b источника:

 U_ab = I·R_Н.

Однако энергетические соотношения в двух схемах замещения реальных источников энергии не одинаковы. Не равны между собой мощности, развиваемые источником ЭДС (рис. 1.3,а) Е·I и источником тока (рис. 1.3,б) U·I.

 

1.3. Эквивалентные преобразования линейных электрических схем

Электрические цепи подразделяются на неразветвленные и разветвлен­ные. Примером простейшей неразветвленной цепи служит схема рис. 1.1,а. По всем ее элементам протекает один и тот же ток. Наиболее распространены разветвленные электрические цепи, имеющие ветви и узловые точки. Токи, протекающие по ветвям схемы, и напряжения на них различны и зависят от состава элементов схемы. Как правило, для упрощения расчета электрических схем применяют их эквивалентные преобразования. Необходимым и достаточным условием эквивалентности исходной и преобразованной схем является неизменность потенциалов и токов в местах присоединений преобразуемой части схемы.

 

Преобразования схем без источников

а) По последовательно соединенным сопротивлениям протекает один и тот же ток:

 

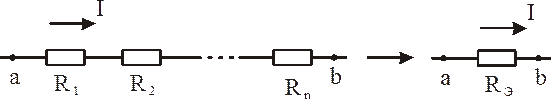
                                              Рис. 1.4

где  - эквивалентное сопротивление, а n – число сопротивлений между точками а и b.

 

б) На параллельно соединенных сопротивлениях одинаковое падение на­пряжения (разность потенциалов):

 

Uab

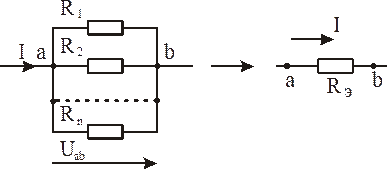
                                                        Рис. 1.5

 

,

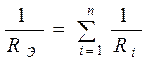где n – число параллельно соединенных сопротивлений.

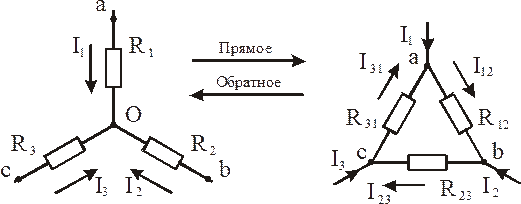
в) Преобразование звезды из трех сопротивлений в треугольник и обратное.

Трехлучевая звезда (рис. 1.6, а) имеет общую точку «О». Преобразования будут эквивалентными, если в схемах, изображенных на рис. 1.6, а, б, токи I₁, I₂, I₃ и напряжения U_ab, U_bc, U_ca будут одинаковыми.

 

                       а)                                                      б)

                                                    Рис.1.6

 

При прямом преобразовании звезды в треугольник надо выразить сопро­тивления R₁₂ , R₂₃ , R₃₁ через R₁ , R₂ и R₃ следующим образом:

                                

       

                                      

 

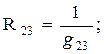
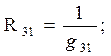
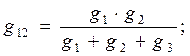
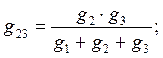
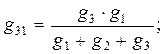
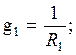
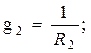
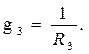
При обратном преобразовании треугольника в звезду надо выразить сопротивления R₁ , R₂ и R₃ через R₁₂ , R₂₃ , R₃₁ следующим образом:

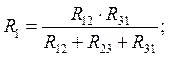
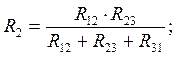
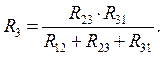
Преобразование схем с источниками

а) Переход от схемы с источником ЭДС к схеме с источником тока и обратно.

 

 

 

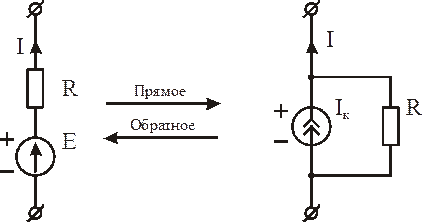
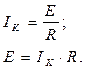
                             Рис. 1.7

б) Преобразование нескольких параллельных ветвей с источниками к одной эквивалентной рассматривается в методе двух узлов (раздел 1.5).

 

Законы Ома и Кирхгофа

На базе этих законов рассчитываются все электрические цепи как линейные, так и нелинейные.

Закон Ома для участка цепи, не содержащего источник ЭДС (рис. 1.8), устанавливает связь между током I и напряжением U_ab на этом участке. Ток I течет от более высокого потенциала j_а точки а к более низкому потенциалу

     Рис. 1.8         j _b точки b. Под действием разности потенциалов j_а - j _b   

создается падение напряжения или просто напряжение на сопротивлении R:

 

 

 

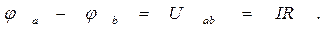
Положительное направление напряжения U_ab на рис. 1.8 показано стрелкой от точки a к точке b.

Закон Ома формулируется: ток прямопропорционален напряжению на участке цепи и обратнопропорционален его сопротивлению: I=U_ab/R.

Рассмотрим закон Ома для участка цепи, содержащего источник ЭДС (рис. 1.9, а, б).

 

                             а)                                               б)

                                                       Рис. 1.9

(1.1)

Учитывая, что источник ЭДС идеальный, а ток течет от точки а к точке с,  напряжение U_ac для схемы рис. 1.9,а запишется:

(1.2)

В уравнении (1.1) ЭДС взята со знаком минус, так как направлена от точки а, которая в индексах напряжения U_ac записана первой. Из этого уравнения ток выражается как:

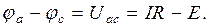
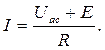
При смене направления тока I (пунктирная стрелка) в схеме рис.1.9,а напряжение U_ac и ток I соответственно запишутся:

(1.3)

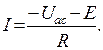
В схеме рис. 1.9,б ЭДС взята со знаком плюс, так как направлена к точке а, которая в индексах напряжения U_ac записана первой. При протекании тока от точки а к точке с напряжение U_ac и ток I соответственно запишутся:

(1.4)

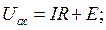
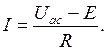
При смене направления тока (пунктирная стрелка) в схеме рис. 1.9,б напряжение U_ac и ток I имеют вид:

(1.5)

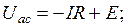
Ток, записанный по уравнениям (1.2…1.5), отражает закон Ома для участка цепи, содержащего источник ЭДС.

Существуют два закона Кирхгофа.

Первый закон Кирхгофа формулируется: алгебраическая сумма токов в узле электрической цепи:

(1.6)

                                                                   

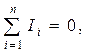
где n – число токов, при этом со знаком плюс записываются токи на правленые к узлу, а со знаком минус – от узла.

 

Второй закон Кирхгофа формулируется: алгебраическая сумма падений напряжений на сопротивлениях в любом замкнутом контуре равняется алгебраической сумме ЭДС вдоль того же контура:

(1.7)

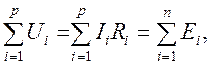
где p – число сопротивлений в контуре,

n – число ЭДС в контуре.