Пространственная оптимизация – решение задачи направленной на получение максимального суммарного прироста капитала при реализации нескольких независимых тнвестиционных проектов, стоимость которых превышает имеющиеся у инвестора финансовые ресурсы.
Пространственная оптимизация для проектов поддающихся дроблению:
1) для каждого проекта расчитывается NPV и индекс доходности PI (ранжируем по PI);
2) проекты ранжируются по степени убывания показателя PI;
3) к реализации принимаются первые x проектов, стоимость которых в смме не превышают лимита сроков предназначенных для инвестирования;
4) при наличии остатка инвестиционных средств они вкладываются в очередной проект, но не в полном объеме, а лишь в той части, в которой он может юыть профинансирован;
5) рассчитывается суммарный NPV для выбранных проектов
Пример. Фирма планирует инвестировать в ОФ 60 млн.д.е. Цена источника финансирования 10%. Рассматривается 4 проекта.
| Проект | 0 | 1 | 2 | 3 | 4 |
| А | -35 | 11 | 16 | 18 | 17 |
| Б | -25 | 9 | 13 | 17 | 10 |
| В | -45 | 17 | 20 | 20 | 20 |
| Г | -20 | 9 | 10 | 11 | 11 |
NPVA = 11*0,909+16*0,826+18*0,751+17*0,683-35=13,34
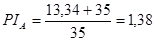 3
3
NPVБ = 13,52 PIБ =1,54 2
NPVB =15,65 PIB =1,35 4
NPVГ = 12,22 PIГ = 1,61 1
Оптимальная инвестиционная стратегия
| Проект | I | Часть инвестиций включенных в инвестиционный проект, % | Чистая текущая стоимость NPV, млн.долл. |
| Г | 20 | 100 | 12,22 |
| Б | 25 | 100 | 13,52 |
| А | 60-(20+25)=15 | 15/35(100%)=42,86 | 13,34*0,4286=5,72 |
| Итого | 31,46 |
Оптимизация для проектов неподдающихся дроблению
В случае, когда проект может быть принят только в полном объеме необходимо провести просмотр сочетаний проектов с расчетом их суммарного NPV. Комбинация обеспечивающая max значение суммарного NPV счтается оптимальной.
Пример. Используя данные предыдущего примера составить план оптимального размещения инвестиций, если lim инвестиций не должен превышать 60 т.р., а к реализции могут быть приняты проекты только в полном объеме.
| Сочитание проектов | Суммарные инвестиции | Сумарные NPV |
| А+Б | 60 | 26,86 |
| А+В | 80 | сочитание невозможно |
| А+Г | 55 | 25,56 |
| Б+В | 70 | сочитание невозможно |
| Б+Г | 45 | 25,74 |
| В+Г | 65 | сочитание невозможно |
Сочитание А+Б будет оптимальным.
Временная оптимизация
Под временной оптимизацией понимается задача, когда в результате ограниченности ресурсов проекты не могут быть реализованы в планируемом году единовременно, но в следующем году проекты или их часть могут быть реализованы.
Решение.
1) По каждому проекту расчитывается индекс возможных потерь – характеризует относительную потерю NPV в случае если проект будет отсрочен к исполнению на год.
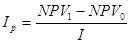
NPV1 – чистая текущая стоимость проекта в случае инвестирования в текущем году,
NPV2 – чистая текущая стоимотьпроекта в случае инвестирования через год.
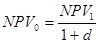
2) Реализация проектов обладающих наименьшей величиной индекса потерь переносится на следующий год.
Пример. По условиям предыдущего примера составить оптимальный план размещений инвестиций на 2 года при условии, что инвестиции на планируемый год не могут превышать 75 млн.д.е.
| Проекты | NPV1 | Коэффициенты дисконтирования d = 10% | NPV0 | NPV1 – NPV0 | Величина отложенных инвестиций на год | In |
| А | 13,34 | 0,909 | 12,13 | 1,21 | 35 | 0,0346 |
| Б | 13,52 | 0,909 | 12,29 | 1,23 | 25 | 0,0492 |
| В | 15,65 | 0,909 | 14,23 | 1,42 | 45 | 0,0316 |
| Г | 12,22 | 0,909 | 11,10 | 1,12 | 20 | 0,0560 |
I – это величина относительных инвестиций
Вывод: наименьшие потери связаны с переносом на следующий год проекта В. А в текущем году реализуем Б и Г. Их суммарное инвестирование составляет 45 млн. д.е. Отсюда, если проект А поддается дроблению, часть его можно также реализовать в текущем году.
Дата: 2019-12-10, просмотров: 472.