Задание. Реализуйте все нижеприведенные шаги в табличном процессоре Excel, необходимые для решения задачи ЛП табличным симплекс-методом, применяя метод искусственного базиса.
Поясним последовательность действий при решения задачи ЛП методом искусственного базиса (М-методом) на примере.
Задача. Решить задачу табличным симплекс-методом [8].
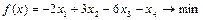
при ограничениях
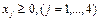
Порядок выполнения работы:
I. Проверка выполнения условий, необходимых для решения задачи табличным симплекс-методом.
1. 
.
2. Задача не является канонической, приведите ее к канонической форме.
Переведите исходную функцию 
на максимум.
Избавьтесь от неравенств во втором и третьем ограничении способом, указанным в 2.1.
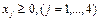
3. В ограничениях 1 и 2 есть базисные переменные: 
- в первом,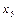 
- во втором, в третьем ограничении нет базисной переменной, следовательно, необходимо применить М-метод.
Составьте расширенную задачу, добавив искусственные переменные к тем ограничениям, где нет базисных переменных.
Расширенная задача:
, 
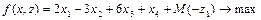
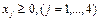4. В целевой функции расширенной задачи есть базисные переменные. Выполните условие, выразив базисные переменные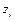 
и 
через небазисные. Подставьте выражения в целевую функцию.
,
.
Таким образом, получите задачу линейного программирования, для которой выполняются все 4 условия.
,
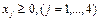II. Оформление исходных данных.
1. Откройте табличный процессор Excel и введите заголовок Метод искусственного базиса.
2. Заполните начальную симплекс-таблицу, таким же образом как в лабораторной работе №4, добавив в нее столбец для переменно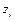й и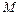 
-строку (рис. 42).
Рис. 42. Исходная симплекс таблица.
11. Проконтролируйте правильность заполнения таблицы. Так как , , 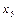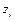- базисные переменные, то на пересечении (5 строка) с (столбец F) должна стоять 1 (ячейка F5), а в соответствующем столбце ниже – нули, на пересечении 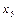(6 строка) с 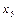(столбец G) должна стоять 1 (ячейка G6), а в соответствующем столбце ниже – нули, 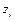(7 строка) с 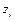(столбец I) должна стоять 1 (ячейка I7), а в соответствующем столбце ниже – нули.
3. Запишите значение целевой функции, начальный опорный план, опираясь на столбец свободных членов (рис. 43).
Рис. 43. Значение целевой функции и начальный опорный план.
III. Нахождение оптимального плана и оптимального значения целевой функции.
1. Так в индексной строке есть отрицательный коэффициент при переменной, то опорный план не является оптимальным. Организуйте процесс улучшения плана, выполнив предложенные шаги.
2. В индексной строке найдите отрицательные элементы. Составьте выражения, учитывая 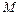-строку. Получите 
.
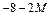В данном случае один отрицательный элемент – это выражение 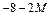, которое соответствует переменной 
.
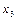3. Соответствующий столбец назовите ведущим. Данный столбец показывает, какую переменную необходимо включить в базис (рис. 44).
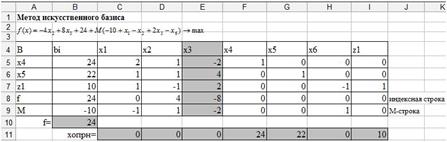
Рис. 44. Ведущий столбец.
4. Определите какую переменную необходимо исключить из базиса. Для этого составьте отношения для всех элементов столбца свободных членов (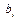 
) к соответствующим элементам ведущего столбца ( 
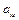). Найдите ведущую строку и ведущий элемент (рис. 45).
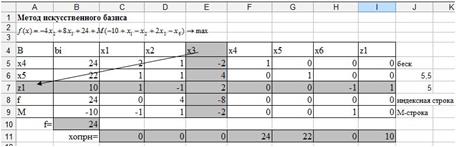
Рис. 45. Ведущая строка и ведущий столбец.
5. Постройте новую симплексную таблицу. Выведите переменную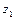 
из базиса, на ее место запишите ту переменную, которой соответствует ведущий столбец. Выполните симплексные преобразования, таким же образом, как и в лабораторной №4, получите базисный столбец, который соответствует переменной 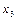. Значения столбца 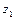можно удалить, так как переменная вышла из базиса (рис. 46).
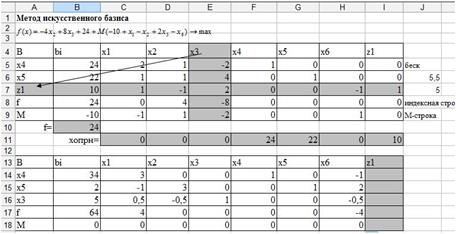
Рис. 46. Первая и вторая симплексные таблицы.
6. Так как в 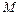-строке все нули, то ее можно удалить из таблицы и получить таблицу, в которой будет только функция 
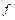(рис. 47).
Рис. 47. Симплексная таблица.
7. В индексной строке есть отрицательные коэффициенты при переменных, опорный план не является оптимальным.
8. Запишите значение целевой функции, найденный новый опорный план, опираясь на столбец свободных членов (рис. 48). Проконтролируйте, что значение целевой функции максимизируется.
9. Организуйте процесс улучшения плана, выполнив те же шаги, до тех пор, пока не будет выполняться какой-нибудь из критериев остановки, получите новую таблицу (рис. 48).
Рис. 48. Симплексные таблицы.
10. В индексной строке нет отрицательных элементов, поэтому план 
оптимален, 
. Так как в исходной задаче функция стремится к минимуму, то 
Задание. Воспользуйтесь материалами лабораторной работы №3. Выполните проверку, используя программу MathCad.
Задания для самостоятельной работы
1. Составьте для нижеприведенных текстовых задач экономико-математическую модель.
2. Решите каждую задачу табличным симплекс-методом пошагово в Excel, опираясь на материалы лабораторных работ №4 и №5.
3. Сравните полученные ответы.
Задача 1. Цех может производить стулья и столы. На производство стула идет 5 единиц материала, на производство стола - 20 единиц (футов красного дерева). Стул требует 10 человеко-часов, стол - 15. Имеется 400 единиц материала и 450 человеко-часов. Прибыль при производстве стула - 45 у.е., при производстве стола - 80 у.е. Сколько необходимо изготовить стульев и столов, чтобы получить максимальную прибыль?
Задача 2. Для изготовления различных изделий A и B используется 2 вида сырья. На производство единицы изделия A его требуется затратить: первого вида – 15 кг, второго вида – 11 кг, третьего вида – 9 кг. На производство единицы изделия B требуется затратить сырья первого вида – 4 кг, второго вида – 5 кг, третьего вида – 10 кг.
Производство обеспечено сырьем первого вида в количестве 1095 кг, второго вида – 865 кг, третьего вида – 1080 кг.
Прибыль от реализации единицы готового изделия А составляет 3 рубля, изделия B – 2 рубля. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
Задача 2. Нефтеперерабатывающий завод располагает двумя сортами нефти: А - 10 ед., В - 15 ед. При переработке из нефти получается бензин (Б) и мазут (М). Имеется три варианта технологического процесса переработки:
I: 1 ед. А + 2 ед. В дает 3 ед. Б + 2 ед. М;
II: 2 ед. А + 1 ед. В дает 1 ед. Б + 5 ед. М;
III: 2 ед. А + 2 ед. В дает 1 ед. Б + 2 ед. М.
Цена мазута – 1 долл. за единицу, цена бензина – 10 долл. за единицу. Найти наиболее выгодный технологический процесс переработки имеющегося количества нефти [10].
(М-метод) Задача 2. Изделия трех видов (А, B, C) вырезаются из стальных листов. Предприятие имеет 150 стальных листов. Каждый лист можно раскроить одним из трех способов. Количество изделий, получаемых из одного листа, и величины отходов для каждого способа раскроя приведены в таблице.
| Количество изделий | Способы раскроя | ||
| А | |||
| B | |||
| C | |||
| Отходы |
Предприятию необходимо раскроить листы таким образом, чтобы отходы были минимальны. При этом необходимо выпустить не менее 400 изделий A, не менее 250 изделий B и не более 300 изделий C (последнее требование связано с тем, что спрос на изделия C ограничен) [11].
(М-метод) Задача 3.Продукцией городского молочного завода являются молоко, кефир и бифидок, расфасованные в бутылки. На производство 1 т молока, кефира и бифидока требуется соответственно 1010, 1010 и 9450 кг молока. При этом затраты рабочего времени при разливе 1 т молока и кефира составляют 0,18 и 0,19 машино-часов. На расфасовке 1 т бифидока заняты специальные автоматы в течение 3,25 часов. Всего для производства цельномолочной продукции завод может использовать 136000 кг молока. Основное оборудование может быть занято в течение 21,4 машино-часов, а автоматы по расфасовке бифидока – в течение 16,25 часов. Прибыль от реализации 1 т молока, кефира и бифидока соответственно равна 30, 22 и 136 руб. Завод должен ежедневно производить не менее 100 т молока, расфасованного в бутылки. На производство другой продукции не имеется никаких ограничений.
Требуется определить, какую продукцию и в каком количестве следует ежедневно изготовлять заводу, чтобы прибыль от ее реализации была максимальной.
(М-метод) Задача 4.
Стандартом предусмотрено, что октановое число автомобильного бензина А-76 должно быть не ниже 76, а содержание серы в нем – не более 0,3 %. Для изготовления такого бензина на заводе используется смесь из четырех компонентов. Данные о ресурсах смешиваемых компонентов, их себестоимости и их октановом числе, а также о содержании серы приведены в таблице.
| Характеристика | Компонент автомобильного бензина | |||
| №1 | №2 | №3 | №4 | |
| Октановое масло | ||||
| Содержание серы, % | 0,35 | 0,35 | 0,3 | 0,2 |
| Ресурсы, т | ||||
| Себестоимость, ден. ед./т |
Требуется определить, сколько тонн каждого компонента следует использовать для получения 1000 т автомобильного бензина А-76, чтобы его себестоимость была минимальной. [6]
Приложение 1
Приложение 2
Нахождение максимального значения функции
> with(simplex):
Warning, the protected names maximize and minimize have been redefined and unprotected
> f:=x1+2*x2;
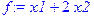
> syst_ogr:={-3*x1+14*x2<=1, x1+x2<=6, x1-x2>=3, x1+4*x2>=4};
> optimum:=maximize(f,syst_ogr,NONNEGATIVE);
> fmax:=subs(x1=83/17,x2=19/17,f);
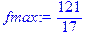
> fmax:=evalf(fmax,4);
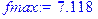
Библиографический список
1. Алесинская Т.В., Сербин В.Д., Катаев А.В. Экономико-математические методы и модели. Линейное программирование: Учебно-методическое пособие по курсу. – Таганрог: Изд-во ТРТУ, 2001. – 79 с.
2. Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие для эконом. спец. вузов. – М.: Высш. шк., 1986. – 319 с.
3. Бразовская Н.В., Бразовская О.В. Методы оптимизации: Учебное пособие / Алт. Госуд. Технич. Ун-т им. И.И. Ползунова. – Барнаул: изд. АлтГТУ, 2006. – 127 с.
4. Буравлева О.Ю. Математические методы в коммерческой деятельности: Учебное пособие. – Тамбов: Изд-во Тамб. гос. техн. ун-та, 2005. – 80 с.
5. Грешилов А.А. Прикладные задачи математического программирования: Учебное пособие. – 2-е изд. – М.: Логос, 206. – 288 с.
6. Деева Е.М. Методические указания по решению типовых задач по дисциплине: «Линейная алгебра и линейное программирование». – Ульяновск: УлГТУ, 2002. – 42 с.
7. Исследование операций в экономике: Учеб. пособие для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ, 2006. – 407 с.
8. Садовничук С.Г. Практические занятия по математическому программированию: Учеб. пособие. – Омск: ОмГПУ: ОмГТУ, 1999. – 84 с.
9. Савотченко С.Е., Кузьмичева Т .Г . Методы решения математических задач в Maple: Учебное пособие. – Белгород: Изд. Белаудит, 2001. – 116 с.
10. Сборник задач и упражнений по высшей математике: Математическое программирование / Под общей ред. А.В. Кузнецова и Р.А. Рутковского. – Мн.: Выш. шк., 2002. – 447 с.
11. Смородинский С.С. Оптимизация решений на основе методов и моделей мат. программирования: Учеб. пособие по курсу «Систем. анализ и исслед. операций» для студ. спец. «Автоматизир. системы обраб. информ.» дневн. и дистанц. форм обуч. / С.С. Смородинский, Н.В. Батин. – Мн.: БГУИР, 2003. – 136 с.
12. Хазанова Л.Э. Математические методы в экономике: учеб. пособие / Л.Э. Хазанова – 3-е изд., стереотип. – М.: Волтерс Клувер, 2005. – 144 с.
Дата: 2016-10-02, просмотров: 246.
