1. Постройте первую полуплоскость в пакете Maple.
Для этого:
-воспользуйтесь возможностями библиотеки plots,которая предназначена для построения различных типов графиков;
-подключите функцию inequal, которая позволяет осуществлять построение полуплоскостей, соответствующих заданным линейным неравенствам, введя нижеприведенную систему предложений;
> plots[inequal]( {-3*x1+14*x2<=1}, x1=-2..8, x2=-2..8, optionsfeasible=(color=grey),
optionsclosed=(color=black, thickness=2),
optionsexcluded=(color=white) );
-нажмите клавишу <Enter>;
-получите первую полуплоскость (рис. 4).
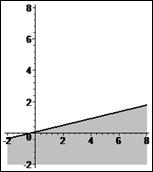
Рис.4. Первая полуплоскость.
Замечание: Формат подключения функции следующий: plots[функция] (параметры). В качестве параметров при подключении функции указывается выводимый объект, интервал изменения переменных, опции вывода. После выполнения команды система Maple переходит в меню графики.
Параметры перечисляются в форме <имя параметра>=<значение>. В нашем случае используются такие имена параметров, как color – цвет, принимающий значения, указанные в таблице 2, а также thickness – толщина линий, принимающий значения 0, 1, 2, 3. В качестве выводимого объекта используется заданная система ограничений. Интервал переменных позволяет управлять границами визуализации полуплоскостей относительно координатных осей. Для изменения цвета полуплоскости и ее границы, задаваемой тем или иным неравенством, применяются определенные опции (таблица 3):
Таблица 3
Опции для изменения цвета полуплоскостей
| optionsfeasible | для областей, которые удовлетворяют всем неравенствам; |
| optionsexcluded | для областей, которые нарушают хотя бы одно неравенство; |
| optionsopen | для линий, которые являются границами областей, описываемых строгиминеравенствами; |
| optionsclosed | для линий, которые являются границами областей, описываемых нестрогиминеравенствами или равенствами; |
Цвет полуплоскости устанавливается параметром color=c, где c– это цвета из таблицы 4.
Таблица 4
Основные цвета
| black | черный |
| blue | синий |
| brown | коричневый |
| green | зеленый |
| grey | серый |
| white | белый |
| yellow | желтый |
2. Аналогичным образом постройте каждую из оставшихся полуплоскостей на осях координат отдельно, поочередно набрав следующие предложения, нажимая клавишу <Enter> после каждого.
> plots[inequal]( {x1+x2<=6}, x1=-2..8, x2=-2..8, optionsfeasible=(color=grey),
optionsclosed=(color=black, thickness=2),
optionsexcluded=(color=white) );
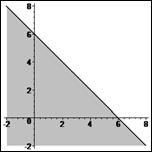
Рис. 5. Вторая полуплоскость.
> plots[inequal]( {x1-x2>=3}, x1=-2..8, x2=-2..8, optionsfeasible=(color=grey),
optionsclosed=(color=black, thickness=2),
optionsexcluded=(color=white) );
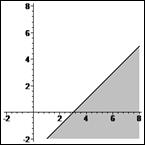
Рис. 6. Третья полуплоскость.
> plots[inequal]( { x1+4*x2>=4}, x1=-2..8, x2=-2..8, optionsfeasible=(color=grey),
optionsclosed=(color=black, thickness=2),
optionsexcluded=(color=white) );
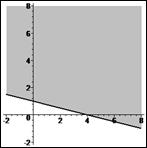
Рис. 7. Четвертая полуплоскость.
3. Постройте полуплоскости в одном окне, добавляя каждый раз по одной, поочередно набрав следующие предложения, нажимая клавишу <Enter> после каждого.
> plots[inequal]( {-3*x1+14*x2<=1, x1+x2<=6}, x1=-2..8, x2=-2..8, optionsfeasible=(color=grey),
optionsclosed=(color=black, thickness=2),
optionsexcluded=(color=white) );
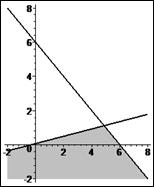
Рис. 8. Первая и вторая полуплоскости.
> plots[inequal]( {-3*x1+14*x2<=1, x1+x2<=6, x1-x2>=3}, x1=-2..8, x2=-2..8, optionsfeasible=(color=grey),
optionsclosed=(color=black, thickness=2),
optionsexcluded=(color=white) );

Рис. 9. Первая, вторая и третья полуплоскости.
> plots[inequal]( {-3*x1+14*x2<=1, x1+x2<=6, x1-x2>=3, x1+4*x2>=4,x1>=0,x2>=0}, x1=-2..8, x2=-2..8, optionsfeasible=(color=grey),
optionsclosed=(color=black, thickness=2),
optionsexcluded=(color=white) );
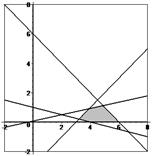
Рис. 10. Область допустимых решений.
4. Присвойте построенной ОДР имя syst_ogr и не выводите изображение на экран.
> syst_ogr:=plots[inequal]( {-3*x1+14*x2<=1, x1+x2<=6, x1-x2>=3, x1+4*x2>=4,x1>=0,x2>=0}, x1=-2..8, x2=-2..8, optionsfeasible=(color=grey),
optionsclosed=(color=black, thickness=2),
optionsexcluded=(color=white) ):
Дата: 2016-10-02, просмотров: 299.