Задание. Реализуйте все нижеприведенные шаги в табличном процессоре Excel, необходимые для решения задачи ЛП.

Поясним последовательность действий при решения задачи ЛП табличным симплекс-методом на примере.

Задача. Решить задачу табличным симплекс-методом [8].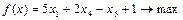

при ограничениях

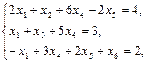
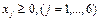
Порядок выполнения работы:

I. Проверка выполнения условий, необходимых для решения задачи табличным симплекс-методом в чистом виде.

1. .

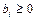2. Задача каноническая.

3. В каждом ограничении есть базисная переменная: 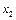- в первом, 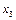- во втором, 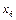- в третьем.

4. В целевой функции нет базисных переменных.

II. Оформление исходных данных.

1. Откройте табличный процессор Excel и введите заголовок Табличный способ решения задач линейного программирования.

2. Заполните начальную симплекс-таблицу.

Шапка таблицы: столбец базисных переменных (B), столбец свободных членов, имеющиеся переменные.

Следующая строка таблицы соответствует первому ограничению. Базисная переменная, найденная в первом ограничении, свободный член, коэффициенты при переменных соответствующего ограничения. Аналогичным образом заполняются 2 и 3 строки.

Последняя строка – это строка целевой функции, которая заполняется следующим образом, свободный член без изменения знака, а коэффициенты при переменных с противоположным (рис. 26).

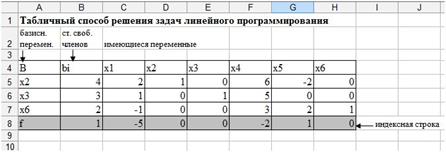
Рис. 26. Исходная симплекс таблица.

5. Проконтролируйте правильность заполнения таблицы. Так как , , 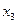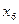- базисные переменные, то на пересечении (5 строка) с (столбец D) должна стоять 1 (ячейка D5), а в соответствующем столбце ниже – нули, на пересечении 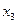(6 строка) с 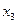(столбец E) должна стоять 1 (ячейка E6), а в соответствующем столбце ниже – нули, 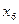(7 строка) с 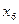(столбец H) должна стоять 1 (ячейка H7), а в соответствующем столбце ниже – нули.

3. Запишите значение целевой функции, начальный опорный план, опираясь на столбец свободных членов (рис. 27).

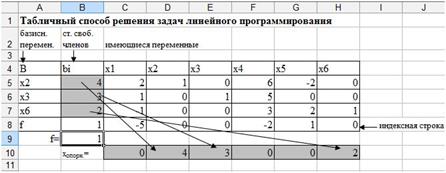
Рис. 27. Значение целевой функции и начальный опорный план.

III. Нахождение оптимального плана и оптимального значения целевой функции.

1. Так в индексной строке есть отрицательные коэффициенты при переменных, то опорный план не является оптимальным. Организуйте процесс улучшения плана, выполнив предложенные шаги.

2. Среди отрицательных элементов индексной строки выберите наибольший по модулю элемент. Соответствующий столбец назовите ведущим. Данный столбец показывает, какую переменную необходимо включить в базис (рис. 28).

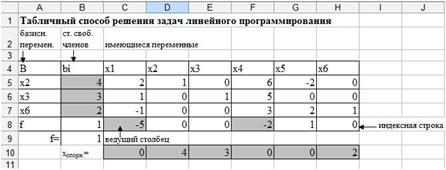
Рис. 28. Выбор ведущего столбца.

3. Теперь необходимо определить какую переменную исключить из базиса. Для этого составьте отношения для всех элементов столбца свободных членов ( 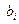) к соответствующим элементам ведущего столбца ( 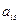). Например, в ячейку I5 введите формулу =B5/C5. Растяните формулы для ячеек I6, I7, исключая ячейку индексной строки (рис. 29).

Рис. 29. Составление отношений.

4. Определите результат отношений (таблица 5), учитывая, что в результате может получиться число, отличное от нуля, 0 или бесконечность (рис. 30).

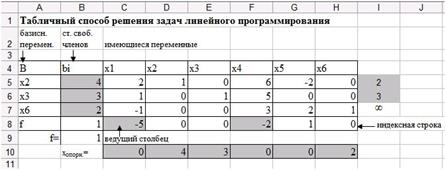
Рис. 30. Результат отношений.

5. Выберите наименьшее из отношений. Строку, в которой получился наименьший результат, назовите ведущей (рис. 31). Данная строка показывает, какую переменную необходимо исключить из базиса.

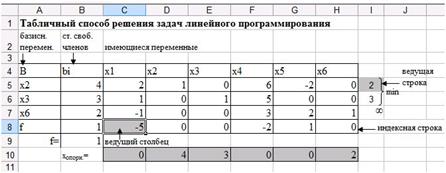
Рис. 31. Выбор ведущей строки.

6. На пересечении ведущей строки и ведущего столбца получается ведущий элемент (рис. 32).

Рис. 32. Ведущий элемент.

7. Постройте новую симплексную таблицу. Выведите переменную из базиса, на ее место запишите ту переменную, которой соответствует ведущий столбец (рис. 33). В нашем случае – это переменная .

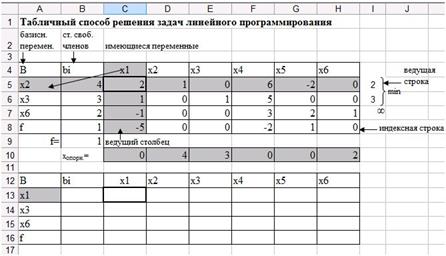
Рис. 33. Новый базис.

8. Так как теперь - базисная переменная, то на пересечении (13 строка) с (столбец C) должна стоять 1 (ячейка С13), а в соответствующем столбце ниже – нули. С помощью элементарных преобразований сделайте ведущий столбец базисным.

Для получения 1 в ячейке С13 необходимо каждый элемент ведущей строки поделить на ведущий элемент.

В ячейку С13 запишите формулу = С5/2 (рис 34), нажмите Enter.

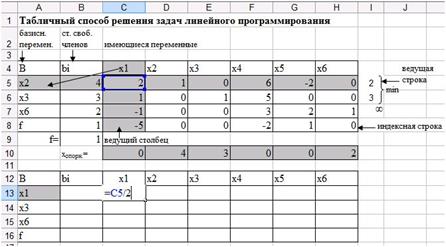
Рис. 34. Получение 1 в ячейке С13.

Растяните формулу (рис. 35).

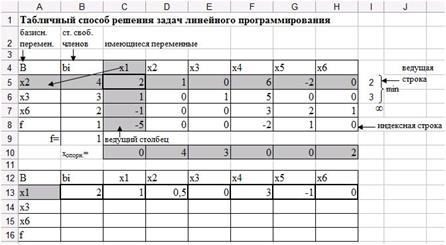
Рис. 35. Первая строка второй симплексной таблицы.

Затем получите нуль в ячейке С14.

Для этого во второй симплексной таблице 1 (ячейка С13) умножьте на элемент предыдущей таблицы, соответствующий элементу ячейки С14, взятый с противоположным знаком и сложите с этим же элементом.

Так как элемент, соответствующий элементу ячейки С14 равен 1 (ячейка С6), то это означает, что все элементы первой строки второй симплексной таблицы умножаются на (-1) и складывается с соответствующими элементами первой симплексной ьаблицы. Запишите в ячейку С14 формулу =C13*(-1)+C6 (рис. 36).

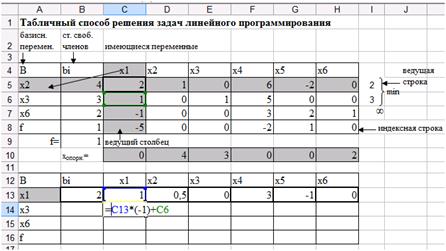
Рис. 36. Элемент С14 второй симплексной таблицы.

Аналогичным образом получите остальные элементы базисного столбца (рис. 37 и рис. 38).

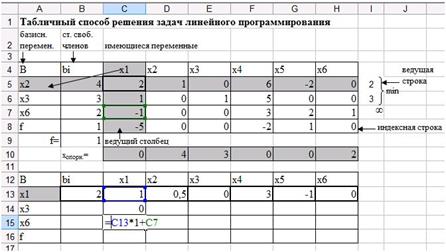
Рис. 37. Элемент С15 второй симплексной таблицы.

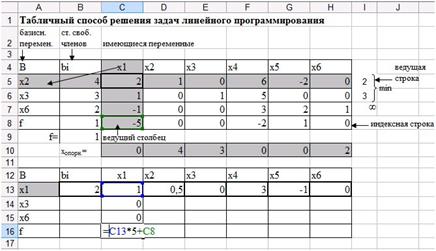
Рис. 38. Элемент С16 второй симплексной таблицы.

9. Растяните формулы базисного столбца по строкам, получите вторую симплексную таблицу (рис. 39).

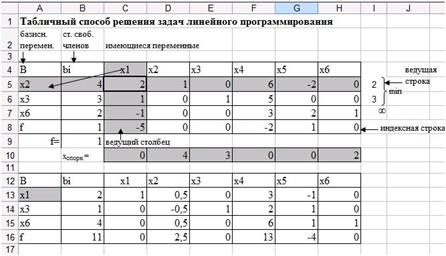
Рис. 39. Первая и вторая симплексные таблицы.

10. Так в индексной строке есть отрицательные коэффициенты при переменных, то опорный план не является оптимальным.

11. Запишите значение целевой функции, найденный новый опорный план, опираясь на столбец свободных членов (рис. 40). Проконтролируйте, что значение целевой функции максимизируется.

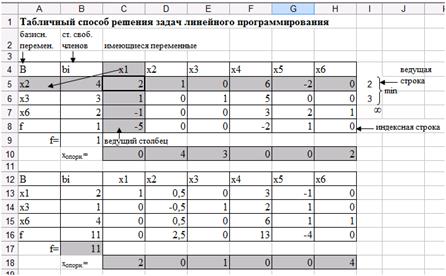
Рис. 40. Значение целевой функции и опорного плана второй симплексной таблицы.

12. Организуйте процесс улучшения плана, выполнив предложенные шаги, начиная с пункта 5, до тех пор пока не будет выполняться какой-нибудь из критериев остановки. Получите третью симплексную таблицу (рис. 41).

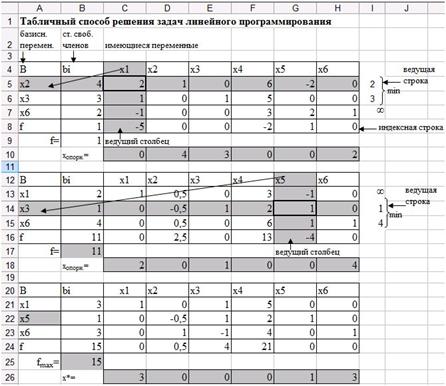
Рис. 41. Первая, вторая и третья симплексные таблицы.

13. В индексной строке нет отрицательных элементов, поэтому план 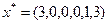оптимален, .

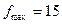Задание. Воспользуйтесь материалами лабораторной работы №3. Выполните проверку, используя программу MathCad.