Для использования табличного симплекс-метода в чистом виде задача ЛП, должна удовлетворять следующим 4 условиям:

1. правые части всех уравнений системы неотрицательны ( );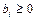

2. задача каноническая, т.е. система ограничений должна быть представлена в виде уравнений, исходная функция направлена на ;

3. в каждом уравнении системы есть базисная переменная;

4. целевая функция выражена через небазисные переменные.

Рассмотрим возможные действия, если не выполняется 1 условие.

Если 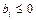, то умножьте соответствующее ограничений на (-1), а затем продолжите проверку остальных условий.

Рассмотрим возможные действия, если не выполняется 2 условие.

Если не выполняется условие – задача каноническая, то необходимо привести задачу линейного программирования к канонической форме.

Задача представлена в канонической форме, если она соответствует следующим условиям:

- целевая функция подлежит максимизации;

- все ограничения имеют вид равенств;

- на все переменные накладываются условие неотрицательности.

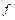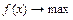Если целевая функция задачи подлежит минимизации, то для перехода к целевой функции, подлежащей максимизации, необходимо умножить исходную целевую функцию на –1. Доказано, что максимальное значение любой функции всегда равно минимальному значению функции , взятому с обратным знаком. Таким образом, если , то .

Для преобразования ограничения «больше или равно» в равенство (т.е. в ограничение «равно») необходимо вычесть из левой части ограничения дополнительную переменную.

Для преобразования ограничения «меньше или равно» в равенство необходимо прибавить к левой части ограничения дополнительную переменную. На все переменные, используемые для приведения задачи к канонической форме, накладываются условия неотрицательности. Переменные, вычитаемые из ограничений «больше или равно» для их приведения к канонической форме, называются избыточными, а переменные, прибавляемые к ограничениям «меньше или равно» – остаточными.

Если на какую-либо переменную не накладывается ограничение неотрицательности, то она заменяется на разность двух переменных, каждая из которых должна быть неотрицательной. Таким образом, если некоторая переменная 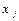может принимать как положительные, так и отрицательные значения, то во всех ограничениях и в целевой функции ее следует заменить на разность двух переменных: 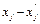, на каждую из которых накладывается условие неотрицательности , .

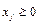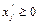Замечание: Если в функции задачи ЛП оформлена реальная производственная ситуация, то дополнительные переменные, которые приходится вводить в модель в процессе преобразования ее к канонической форме, всегда имеет определенный экономический смысл.

Рассмотрим возможные действия, как проверить выполнение 3 условия.

Начальный базис легко определить, если в каждом ограничении имеется переменная, входящая в это ограничение с коэффициентом, равным единице, и при этом не входящая ни в одно из других ограничений. Эти переменные принимаются в качестве базисных. Все остальные (небазисные) переменные принимаются равными нулю. Количество базисных переменных (переменных, составляющих базис), всегда равно количеству ограничений ( 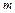). [11]

Замечание. Такой способ определения начального базиса наиболее удобен при решении задач, для которых математическая модель состоит только из ограничений «меньше или равно». В таких задачах после приведения к канонической форме в каждом ограничении имеется переменная, входящая в данное ограничение с коэффициентом, равным единице, и не входящая ни в одно из других ограничений. Эти переменные – остаточные переменные, введенные при приведении задачи к канонической форме. Эти переменные принимаются в качестве базисных. Все остальные переменные, входившие в исходную математическую модель задачи, принимаются в качестве небазисных.

Если условие 3 не выполняется, то использовать табличный симплекс-методом в чистом виде не рекомендуется.

Рассмотрим возможные действия, если не выполняются 4 условие.

Если в целевой функции имеются базисные переменные, то необходимо из соответствующих ограничений выразить базисные переменные через небазисные и подставить полученные выражения в целевую функцию, привести подобные. После преобразований в целевой функции должны быть только небазисные переменные.

Общий алгоритм решениязадачи табличным симплекс-методом в чистом виде.

1. Проверьте выполнение всех условий, если какое-нибудь из условий не выполняются, то проделайте ряд действий для выполнения соответствующего условия; если же невозможно выполнить какое-нибудь из условий, то задачу нельзя решить табличным способом в чистом виде, обратитесь к другому методу.

2. Если выполнены все условия, постройте начальную симплекс-таблицу, в шапку таблицы включите столбец базисных переменных (B), столбец свободных членов, имеющиеся переменные ( 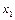, ,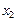…, ), строки таблицы соответствуют соответствующим ограничениям (базисная переменная, найденная в ограничении, свободный член, коэффициенты при переменных). Последняя строка – это строка целевой функции 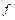(индексная строка), которая заполняется следующим образом, свободный член без изменения знака, а коэффициенты при переменных с противоположным.

3. Проконтролируйте правильность заполнения таблицы; если таблица построена правильно, то в столбце каждой базисной переменной должна присутствовать только одна единица, остальные коэффициенты – нулевые.

4. Проверьте выполнение критериев остановки решения.

5. Если ни один из критериев остановки не выполняется, запишите начальный опорный план значение целевой функции, опираясь на столбец свободных членов.

6. Организуйте процесс улучшения плана следующим образом:

1. среди отрицательных элементов индексной строки выберите наибольший по модулю элемент, соответствующий столбец назовите ведущим; данный столбец показывает, какую переменную необходимо включить в базис;

2. составьте отношения для всех элементов столбца свободных членов ( 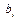) к соответствующим элементам ведущего столбца ( );

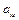3. определите результат отношений (таблица 5);

4. выберите наименьшее из отношений, строку, в которой получился наименьший результат, назовите ведущей; данная строка показывает, какую переменную необходимо исключить из базиса;

5. найдите на пересечении ведущей строки и ведущего столбца ведущий элемент;

6. постройте новую симплексную таблицу, с помощью элементарных преобразований (метод Гаусса) сделайте ведущий столбец базисным;

7. получите новый опорный план.

7. Проверьте найденный опорный план, согласно критериям остановки;

8. Выполняйте пункты 6-7 до получения оптимального решения или заключения, о том, что задача имеет бесконечное множество решений, или не имеет решений.

Таблица 5

Возможные результаты отношения столбца свободных членов и ведущего столбца

Результат	Значения
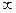
Число, равное .	имеют одинаковые знаки
	имеют разные знаки

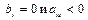
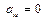
Теорема: Если в индексной строке симплексной таблицы есть отрицательный элемент , а в столбце над ним есть положительные элементы, то существует другой базисный план 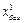, принадлежащий области 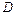, такой, что .

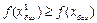Критерии остановки решения задачи линейного программирования табличным симплекс методом[8]

Теорема: (Первый критерий остановки симплекс-метода). Если в индексной строке симплексной таблицы нет отрицательных элементов, то план 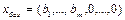оптимален.

Теорема: (Второй критерий остановки симплекс-метода). Если существует столбец такой, что и все числа 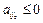, то .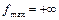

Замечание: Если в индексной строке нет отрицательных элементов, и если при этом нет 0-ых, то оптимальный план единственный, если же есть хотя бы один 0-ой, то оптимальных планов бесконечное множество.

Теорема: (Третий критерий остановки симплекс-метода). Если в какой-нибудь строке симплексной таблицы кроме свободного члена других положительных элементов нет, то система не имеет неотрицательных решений, т.е. система ограничений задачи несовместна.

Замечание: Если в ходе элементарных преобразований получится 0-ая строка, все элементы которой кроме свободного члена 0, то система ограничительных уравнений задачи несовместна.

2.2. Табличный симплекс метод. Метод искусственного базиса (М-метод)

Среди задач линейного программирования встречаются такие задачи, когда не выполняется условие наличия базисной переменной в каждом из ограничений, то есть не выполняется условие 3 для решения задачи табличным симплекс-методом в чистом виде. В таком случае при решении задач линейного программирования необходимо использовать метод искусственного базиса (М-метод).