Задание. Используя MathCad, Maple, Excel, специализированный пакет SimplexWin, найдите оптимальный план и оптимальное значение целевой функции для определенной задачи линейного программирования, выполнив предложенные алгоритмы.
Для организации проверки решения задачи линейного программирования, выполненного вручную целесообразно использовать математические пакеты, которые имеют встроенные функции, позволяющие вычислять оптимальные планы.
Решение оптимизационных задач в системе MathCad
Рассмотрим решение на примере конкретной задачи.
Задача. Найти значения переменных x1и x2, при которых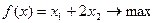 
при ограничениях
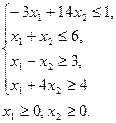
Порядок выполнения работы:
I. Оформление исходных данных.
1. Запустите программу MathCad и введите заголовок Нахождение максимального значения функции.
2. Введите функцию 
.
3. Присвойте начальные значения переменным:
.
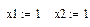II. Решение системы ограничений.
1. Разрешите заданную систему ограничений при помощи команды Given
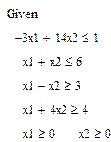
III. Нахождение оптимального плана и оптимального значения целевой функции.
1. Используйте встроенную в пакет MathCad функцию Maximize для нахождения значений переменных x1 и x2, при которых функция f достигает своего максимума.
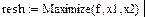
2. Найдите решение
.
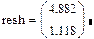3. Подставьте найденные значения в целевую функцию
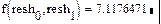
Ознакомиться с вариантом решения задачи ЛП без пояснений можно в приложении.
Решение оптимизационных задач в системе Maple[9]
На примере той же задачи покажем, как найти оптимальный план, используя пакет Maple.
Задача. Найти значения переменных x1и x2, при которых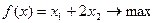
при ограничениях
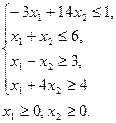
Порядок выполнения работы:
I. Оформление исходных данных.
1. Запустите программу Maple и введите заголовок Нахождение максимального значения функции, используя команду Insert – Text.
2. Подключите библиотеку simplex, предназначенную для оптимизации линейных систем с использованием симплексного алгоритма.
> with(simplex):
Warning, the protected names maximize and minimize have been redefined and unprotected
3. Задайте целевую функцию и систему ограничений.
> f:=x1+2*x2;
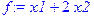
> syst_ogr:={-3*x1+14*x2<=1, x1+x2<=6, x1-x2>=3, x1+4*x2>=4};
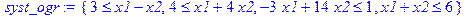
II. Нахождение оптимального плана и оптимального значения целевой функции.
1. Для нахождения максимума целевой функции используйте функцию maximize, формат которой следующий maximize(<функция>, <система ограничений>, <опции>);
При этом условие неотрицательности переменных удобно указать опцией NONNEGATIVE.
> optimum:=maximize(f,syst_ogr,NONNEGATIVE);
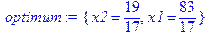
2. Используйте команду subs, которая позволяет подставить значения переменных x1 и x2 в функцию f.
> fmax:=subs(x1=83/17,x2=19/17,f);
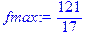
3. Примените функцию evalf для представления ответа в форме действительного числа с 4 значащими цифрами.
> fmax:=evalf(fmax,4);
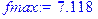
Ознакомиться с вариантом решения задачи ЛП без пояснений можно в приложении.
Решение оптимизационных задач в специализированном пакете SimplexWin. http://www.simplexwin.narod.ru/
Данная программа предназначена для решения задач линейного программирования симплекс методом.
Задача. Найти значения переменных x1и x2, при которых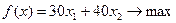 
при ограничениях
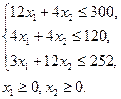
Порядок выполнения работы:
I. Оформление исходных данных.
1. Запустите программу SimplexWin и установите требуемый размер матрицы ограничений, выбрав в меню команду Настройки – Размер матрицы (рис. 13).
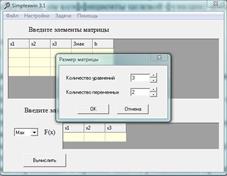
Рис. 13. Определение размера матрицы.
2. Введите данные (рис. 14). Если задача вводится не в канонической форме, то дополнительные переменные и искусственные базисы (а также соответствующие им коэффициенты целевой функции) добавляются автоматически.
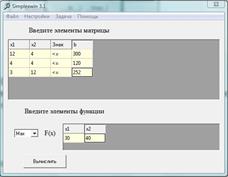
Рис.14. Ввод данных.
II. Нахождение оптимального плана и оптимального значения целевой функции.
1.
 |
Нажмите кнопку Вычислить и получите форму Результаты (рис. 15).
Рис. 15. Форма Результаты.
2. В форме Результаты нажмите кнопку Результат, которая позволяет произвести решение задачи в автоматическом режиме и отобразить на экране последнюю симплексную таблицу и результат (рис. 16).
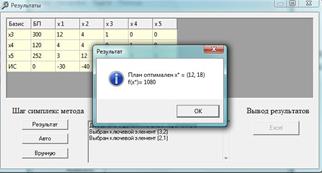
Рис. 16. Решение задачи.
Решение оптимизационных задач в Excel[1]
Рассмотрим пример нахождения для следующей задачи линейного программирования.
Задача. Найти значения переменных x1и x2, при которых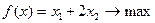 
при ограничениях
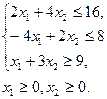
Порядок выполнения работы:
I. Оформление исходных данных.
1. Создайте экранную форму для ввода условий задачи (переменных, целевой функции, ограничений) и введите в нее исходные данные (коэффициенты целевой функции, коэффициенты при переменных в ограничениях, правые части ограничений) (рис. 17).
Рис. 17. Экранная форма задачи (курсор в ячейке D6).
Замечание: В экранной форме на рис. 17 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Так, например, переменным задачи соответствуют ячейки B3 (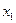 
), C3 ( 
), коэффициентам целевой функции соответствуют ячейки B6 ( 
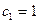), C6 ( 
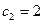), правым частям ограничений соответствуют ячейки F10 ( 
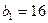), F11 ( 
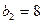),F12 ( 
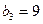) и т.д.
2. Введите зависимости из математической модели в экранную форму, т.е. введите формулу для расчета целевой функции и формулу для расчета значений левых частей ограничений.
Согласно условию задачи значение целевой функции определяется выражением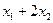 
. Используя обозначения соответствующих ячеек в Excel, формулу для расчета целевой функции можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3), на соответствующие ячейки, отведенные для коэффициентов целевой функции (B6, C6).
Для того чтобы задать формулу зависимости для целевой функции проделайте следующее:
– поставьте курсор в ячейку D6;
– вызовите окно Мастер функций – шаг 1 из 2, нажав кнопку 
на стандартной панели инструментов;
– выберите в окне Категориякатегорию Математические;
– в окне Функциявыберите функцию СУММПРОИЗВ;
– в появившемся окнеСУММПРОИЗВ в строку Массив 1введите выражение B$3:C$3, а в строку Массив 2 – выражение B6:С6;
– нажмите кнопку OK.
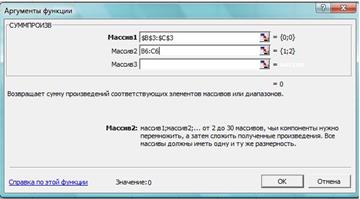
Рис. 18. Ввод формулы для расчета ЦФ в окне Мастер функций.
После ввода ячеек в строки Массив 1 и Массив 2в окне СУММПРОИЗВ появятся числовые значения введенных массивов (рис. 18), а в экранной форме появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые) (рис. 19).
Замечание: Символ $ перед номером строки означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится. Символ :означает, что в формуле использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия.
Левые части ограничений задачи представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, C10 – 1 ограничение; B11, C11 – 2 ограничение; B12, C12 – 3 ограничение).
Формулы, задающие левые части ограничений задачи, отличаются друг от друга и от формулы в целевой ячейке D6только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничении достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений.
Для расчета значений левых частей ограничений выполните следующее:
– поставьте курсор в ячейку D6 и скопируйте в буфер содержимое ячейки (клавишами Ctrl+C);
– поставьте курсор поочередно в поля левой части каждого из ограничений, то есть D10,D11, D12, и вставляйте в эти поля содержимое буфера (клавишами Ctrl+V) (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера).
После ввода на экране в полях D10,D11, D12появится 0 (нулевое значение) (рис. 19).
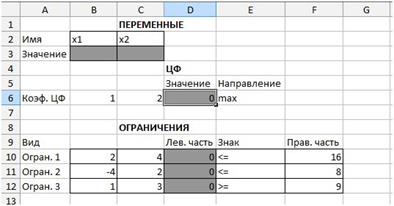
Рис. 19. Экранная форма задачи после вода
всех необходимых формул.
3. Проверьте правильность введения формул.
Для этого:
– произведите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами, при этом на экране рамкой будут выделяться ячейки, используемые в формуле (рис. 20 и рис. 21).
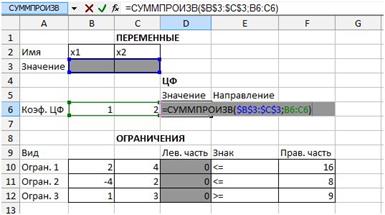
Рис. 20. Проверка правильности введения
формулы в целевую ячейку D6.
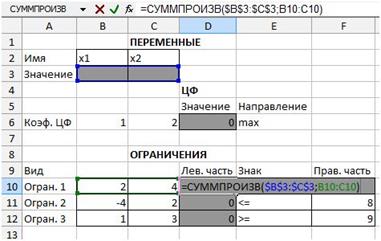
Рис. 20. Проверка правильности введения
формулы в ячейку D10 для левой части ограничений.
4. Задайте целевую функцию и введите ограничения в окне Поиск решения(рис. 21).
Для этого:
– поставьте курсор в ячейку D6;
– вызовите окно Поиск решения, выбрав на панели инструментов Данные – Поиск решения;
– поставьте курсор в поле Установить целевую ячейку;
– введите адрес целевой ячейки $D$6или сделайте одно нажатие левой клавишей мыши на целевую ячейку в экранной форме, что будет равносильно вводу адреса с клавиатуры;
– укажите направление оптимизации целевой функции, щелкнув один раз левой клавишей мыши по селекторной кнопке максимальному значению;
– в окне Поиск решенийв поле Изменяя ячейкивведите ячейки со значениями переменных $B$3:$C$3, выделив их в экранной форме, удерживая левую кнопку мыши;
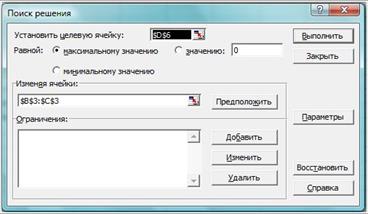
Рис. 21. Окно Поиск решения.
– нажмите кнопку Добавить;
– в полеСсылка на ячейкувведите адрес ячейки левой части конкретного ограничения, например, $D$10;
– в соответствии с условием задачи выберите в поле знака необходимый знак, например, для 1 ограничения это знак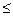 
;
– в поле Ограничениевведите адрес ячейки правой части, рассматриваемого ограничения, например $F$10;
– аналогичным образом установите соотношения между правыми и левыми частями других ограничений ($D$11 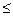$F$11, $D$12 
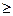$F$12);
– подтвердите ввод всех перечисленных условий нажатием кнопки OK(рис. 22 и рис. 23).
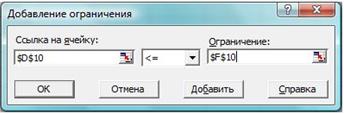
Рис. 22. Добавления условия.
Замечание: Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений, то это можно сделать на жав на кнопки Изменитьили Удалить.
II. Нахождение оптимального плана и оптимального значения целевой функции.
1. Установите параметры решения задачи (рис. 23).
Для этого:
– нажмите кнопку Параметры;
– заполните некоторые поля окна Параметры поиска решения;
– подтвердите установленные параметры нажатием кнопки OK.
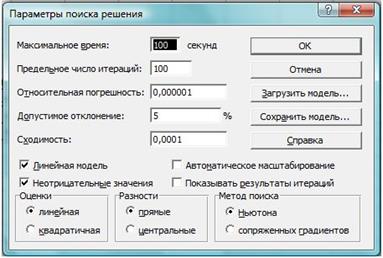
Рис. 23. Параметры поиска решения,
подходящие для большинства задач.
Замечание:
Параметр Максимальное времяслужит для назначения времени (в секундах), выделяемого на решение задачи.
Параметр Предельное число итерацийслужит для управления временем решения задачи путем ограничения числа промежуточных вычислений.
Параметр Относительная погрешностьслужит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличивает время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр Допустимое отклонениеслужит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большого допуска поиск решения заканчивается быстрее.
Параметр Сходимостьприменяется только при решении нелинейных задач.
Установка флажка Линейная модельобеспечивает ускорение поиска решения линейной задачи за счет применения симплекс-метода.
Установка флажка Неотрицательные значенияпозволяет ограничить условия для допустимых значений переменных.
Запустите задачу на решение.
2. Запустите задачу на решение.
Для этого:
– нажмите кнопку Выполнить(рис. 24);
Рис. 24. Сообщение об успешном решении задачи
Замечание:
После запуска на решение задачи ЛП на экране появляется окно Результаты поиска решения с одним из сообщений, следующих сообщений:
1. Решение найдено. Все ограничения и условия оптимально выполнены. Сообщение об успешном решении задачи.
2. Поиск не может найти подходящего решения. Сообщение при несовместной системе ограничений задачи.
3. Значения целевой ячейки не сходятся. Сообщение при несовместной системе ограничений задачи.
В окне Результаты поиска решения представлены названия трех типов отчетов: Результаты, Устойчивость, Пределы. Они необходимы при анализе полученного решения на чувствительность.
– нажмите кнопку OK, в экранной форме появится оптимальное решение задачи (рис. 25).
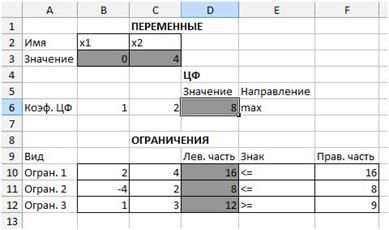
Рис. 25. Экранная форма задачи после получения решения.
Задания для самостоятельной работы
1. Составьте для нижеприведенных текстовых задач экономико-математическую модель.
2. Решите каждую задачу в MathCad, Maple, Excel, специализированном пакете SimplexWin, используя материалы лабораторной работы №3.
3. Сравните полученные ответы.
Задача 1. Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и, после соответствующей обработки, поступают в продажу. Хотя недельный расход корма для цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 у.е. Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов. В качестве ингредиентов рассмотрим три: известняк, зерно и соевые бобы. Требования к питательности рациона сформулируем, учитывая три вида питательных веществ: кальций, белок и клетчатку. В таблице приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента. Заметим, что известняк не содержит ни белка, ни клетчатки.
| Ингредиент | Содержание питательных веществ, у.е./кг ингредиента | Стоимость, у.е./кг | ||
| кальций | белок | клетчатка | ||
| известняк | 0,38 | – | – | 0,04 |
| зерно | 0,001 | 0,09 | 0,02 | 0,15 |
| соевые бобы | 0,002 | 0,5 | 0,08 | 0,4 |
Смесь должна содержать: не менее 0,8%, но не более 1,2% кальция; не менее 22% белка; не более 5% клетчатки.
Требуется определить для птицеводческой фермы количество (в кг) каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.
Задача 2. Предприятие выпускает панели для пультов управления двух видов: стандартные (для работы в обычных условиях) и специального исполнения (для работы при повышенных температурах). При изготовлении панелей используется пластмасса и алюминий. Для изготовления одной стандартной панели требуется 12,5 кг пластмассы и 8 кг алюминия; для изготовления одной панели специального исполнения – 7,2 кг пластмассы и 14,5 кг алюминия. Предприятие имеет 300 кг пластмассы и 400 кг алюминия. Прибыль предприятия от выпуска одной стандартной панели составляет 7 ден. ед., прибыль от выпуска одной панели специального исполнения – 9 ден. ед. Требуется определить, сколько панелей каждого вида должно выпускать предприятие, чтобы получить максимальную прибыль.
Руководство к выполнению заданий для самостоятельной работы.
Для нахождения минимального значения целевой функции в системах MathCad и Maple воспользуйтесь функцией minimize, а в программах Excel и SimplexWin не забудьте переключить направление оптимизации
Тема 2. Симплекс-метод.
В предыдущей теме мы рассмотрели такой метод решения задач линейного программирования, как геометрический. Геометрический метод имеет ряд недостатков, к которым можно отнести неточность ручных построений и наличие двух переменных.
В лабораторных работах №1 и №2 мы показали каким образом возможно устранить неточность ручных построений. Применение же симплекс-метода позволит решать задачи линейного программирования любой размерности, т.е. с любым количеством переменных.
Симплекс-метод – это метод целенаправленного перебора опорных планов задачи линейного программирования в направлении улучшения значения целевой функции.
Он позволяет на конечное число шагов расчета либо найти оптимальное решение, либо установить, что оптимального решения не существует[4].
Отметим, что решение задач линейного программирования на основе симплекс-метода состоит в целенаправленном переборе угловых точек. Минимум или максимум целевой функции всегда достигается при значениях переменных 
, 
,…, 
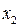, соответствующих одной из угловых точек ОДР. Другими сло-
вами, оптимальное решение всегда находится в угловой точке ОДР. [11]
Дата: 2016-10-02, просмотров: 278.
