1. Проверьте выполнение следующих условий:
- правые части всех уравнений системы неотрицательны ( 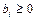 );
);
- задача каноническая, т.е. система ограничений должна быть представлена в виде уравнений, исходная функция направлена на  ;
;
Замечание. Возможные действия, если не выполняется условия 1 и 2 рассмотрены в пункте 2.1.
Таким образом, получите каноническую задачу, в которой все свободные члены положительны.
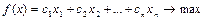
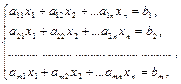

2. Найдите базисные переменные, если они есть, в исходных ограничениях.
3. Найдите ограничение или ограничения, в которых нет базисных переменных, и определитесь с количеством искусственных переменных.
4. Составьте расширенную задачу, добавив искусственные переменные к тем ограничениям, где нет базисных переменных.
Расширенная задача:
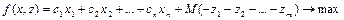
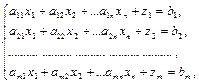
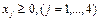 ,
, 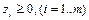 ,
,
где 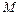 - некоторое достаточно большое число.
- некоторое достаточно большое число.
Замечание. Базисные переменные 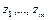 называются искусственными.
называются искусственными.
5. Реализуйте выполнение условия 4, то есть выразите целевую функцию через переменные, не вошедшие в базис.
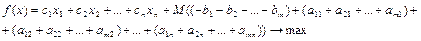
6. Заполните симплексную таблицу, добавив столбцы, отвечающие за искусственные переменные.
7. Включите в симплексную таблицу ниже индексной строки 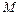 -строку.
-строку.
8. Заполните 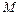 -строку коэффициентами при переменных и свободным членом по такому же правилу, что и в табличном симплекс-методе в чистом виде.
-строку коэффициентами при переменных и свободным членом по такому же правилу, что и в табличном симплекс-методе в чистом виде.
9. Проверьте выполнение критериев остановки решения.
10. Если критерии остановки не выполняются, решайте задачу табличным симплекс-методом, опираясь на опорный план 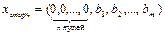 , одновременно ведите преобразования с исходной функцией
, одновременно ведите преобразования с исходной функцией 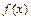 и с
и с 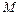 -строкой, до выполнения одного из критериев остановки симплекс-метода.
-строкой, до выполнения одного из критериев остановки симплекс-метода.
Замечание. Для М-метода действуют все критерии остановки решения задачи линейного программирования табличным симплекс методом.
Теорема. Если в оптимальном плане 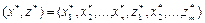 расширенной задачи значения всех искусственных переменных
расширенной задачи значения всех искусственных переменных 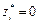 , то
, то 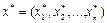
Перед выполнением лабораторных работ ответьте на теоретические вопросы.
Теоретические вопросы
1. Какие условия должны выполняться, для того чтобы можно было решать задачу ЛП табличным симплекс-методом в чистом виде?
2. Каким образом заполняется индексная строка симплексной таблицы?
3. Каков признак существования нового опорного плана, улучшающего целевую функцию?
4. Где записывается начальный опорный план при решении задачи линейного программирования табличным симплекс-методом?
5. Как выбирается ведущий столбец симплексной таблицы?
6. Что показывает выбранный ведущий столбец симплексной таблицы?
7. Как выбирается ведущая строка симплексной таблицы?
8. Что показывает выбранная ведущая строка симплексной таблицы?
9. Если 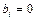 ,
, 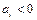 , то чему будет равен результат отношения элемента столбца свободных членов к соответствующему элементу ведущего столбца?
, то чему будет равен результат отношения элемента столбца свободных членов к соответствующему элементу ведущего столбца?
10. Если 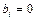 ,
, 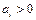 , то чему будет равен результат отношения элемента столбца свободных членов к соответствующему элементу ведущего столбца?
, то чему будет равен результат отношения элемента столбца свободных членов к соответствующему элементу ведущего столбца?
11. Если 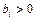 ,
, 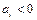 , то чему будет равен результат отношения элемента столбца свободных членов к соответствующему элементу ведущего столбца?
, то чему будет равен результат отношения элемента столбца свободных членов к соответствующему элементу ведущего столбца?
12. Если 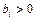 ,
, 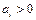 , то чему будет равен результат отношения элемента столбца свободных членов к соответствующему элементу ведущего столбца?
, то чему будет равен результат отношения элемента столбца свободных членов к соответствующему элементу ведущего столбца?
13. В чем смысл первого критерия остановки при решении задачи линейного программирования табличным симплекс методом в чистом виде?
14. В каком случае задача линейного программирования, решаемая табличным симплекс методом, не имеет оптимального решения, но имеет допустимые решения?
15. В каком случае задача линейного программирования, решаемая табличным симплекс методом, не имеет решений?
16. Как будет выглядеть вспомогательная функция для задачи линейного программирования, решаемой М-методом, если нам не хватает в исходной системе ограничений 2 базисные переменные?
17. Какое базисное решение называется реализуемым?
18. Какое базисное решение называется вырожденным?
Дата: 2016-10-02, просмотров: 325.