Существует несколько методов решения задач ЛП. Одним из способов решения задач оптимизации для двух переменных является геометрический метод.
Основные теоремы [7]
Теорема 1. Если задача ЛП имеет оптимальное решение, то целевая функция принимает максимальное значение в одной из угловых точек многоугольника решений, если целевая функция принимает максимальное значение более чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией этих точек.
Данная теорема указывает путь решения задач ЛП, то есть вместо исследования бесконечного множества допустимых решений для нахождения среди них искомого оптимального решения необходимо исследовать только конечное число угловых точек многоугольника решений.
Теорема 2. Каждому допустимому базисному решению в задачи ЛП соответствуют угловая точка многоугольника решений и наоборот каждой угловой точке многоугольника решений соответствует допустимое базисное решение.
Следствие. Если задача ЛП имеет оптимальное решение, то оно совпадает, по крайней мере, с одним из ее допустимых базисных решений.
Вывод:оптимальное значение целевой функции в задаче ЛП следует искать среди конечного числа ее допустимых базисных решений.
Алгоритм решения задач ЛП геометрическим методом[3]:
§ Построение области допустимых решений (ОДР) с учетом системы ограничений.
§ Построение вектора  – вектора наискорейшего возрастания целевой функции.
– вектора наискорейшего возрастания целевой функции.
§ Проведение произвольной линии уровня, перпендикулярной вектору  .
.
§ Определение оптимального плана и оптимального значения целевой функции.
Варианты ОДР:
1. выпуклый многоугольник;
2. выпуклая многоугольная область;
3. пустое множество;
4. единственная точка.
Таблица 2
Соотношение вариантов ОДР и вариантов
оптимальных планов
| Возможные варианты ОДР | Оптимальный план в соответствии с ОДР |
| 1. Выпуклая многоугольная область | 1. Координаты одной из угловых точек, задача имеет единственное решение.
2. Координаты точек отрезка, то есть все точки отрезка оптимальны. Ответ записывается как промежуток между координатами двух точек по оси  и и  , являющихся крайними точками отрезка. , являющихся крайними точками отрезка.
|
| 2. Выпуклая многоугольная область | 1. Координаты одной из угловых точек.
2. 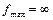 или или  , то есть, задача имеет допустимые решения, но не имеет оптимального плана.
3. Координаты точек отрезка, то есть все точки отрезка оптимальны. , то есть, задача имеет допустимые решения, но не имеет оптимального плана.
3. Координаты точек отрезка, то есть все точки отрезка оптимальны.
|
| 3. Пустое множество | 1. 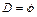 , то есть, у задачи нет планов, она не имеет ни допустимых, ни оптимальных решений. , то есть, у задачи нет планов, она не имеет ни допустимых, ни оптимальных решений.
|
| 4. Единственная точка | 1. Координаты точки. |
Основные трудности, с которыми приходится сталкиваться при реализации геометрического метода, связаны с неточностью ручных построений, а также с нахождением искомой ОДР и определением оптимального плана. Вышеперечисленные проблемы легко разрешимы при помощи использования возможностей математических пакетов.
Математические пакеты предоставляют широкие графические возможности и могут применяться для решения широкого класса задач, в частности, для решения задач линейного программирования геометрическим методом.
Перед выполнением лабораторных работ №1, №2 и №3 ответьте на теоретические вопросы.
Теоретические вопросы
1. Какая задача называется общей задачей линейного программирования?
2. Какая задача называется стандартной?
3. Какая задача называется канонической?
4. Какое решение называется базисным?
5. Что на плоскости задает каждое неравенство системы ограничений?
6. Как построить полуплоскость в заданной системе координат?
7. Какими из перечисленных точек (0,0); (1,-1); (1,1) может задаваться контрольная точка для определения полуплоскости неравенства x1+x2≥0?
8. Что на плоскости может представлять собой область допустимых решений? Какие варианты области допустимых решений возможны?
9. Что на плоскости графически представляет собой целевая функция?
10. Как на плоскости построить вектор 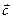 ?
?
11. Что показывает вектор 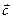 при решении задачи линейного программирования геометрическим методом при целевой функции f(x)=c1x1+c2x2"max?
при решении задачи линейного программирования геометрическим методом при целевой функции f(x)=c1x1+c2x2"max?
12. Как на плоскости построить линии уровня целевой функции?
13. Через какие две точки проходит линия уровня, если ее рассматривать как вектор нормали к вектору 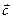 ?
?
14. В чем заключается геометрическая интерпретация нахождения оптимального плана?
15. Что графически представляет собой оптимальный план, если область допустимых решений – выпуклый многоугольник?
16. Какие варианты оптимальных планов возможны?
17. Что означает запись 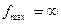 относительно допустимых и оптимальных решений?
относительно допустимых и оптимальных решений?
18. Что означает запись 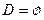 относительно допустимых и оптимальных решений?
относительно допустимых и оптимальных решений?
Дата: 2016-10-02, просмотров: 303.