Замечание:
В связи с тем, что Maple является интерпретатором, следует учитывать, что после ввода и выполнения некоторой команды (группы) можно в любой момент времени вернуться на соответствующую строку, после чего по нажатию на <Enter> команда будет выполнена вновь. При этом в ряде случаев результат будет отличен от предыдущего, так как переменные и прочие конструкции (функции и т.д.) могут иметь уже другое значение.
Для того чтобы очистить значение переменной, необходимо присвоить ей свое собственное имя, записанное в одинарных кавычках.
Для моделирования движения семейства линий уровня выполняется построение множества параллельных прямых при различных значениях параметра с. Изменение параметра с возможно при помощи команды subs(<выражение 1>=<выражение 2>, <выражение 3>), которая позволяет подставлять в выражение 3 вместо выражения 1 выражение2.
1. Очистите значение переменной;
> c:='c':
2. Задайте целевую функцию, присвоив ей имя f1.
> f1:=x1+2*x2=c;
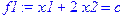
3. Введите уравнение одной линии из семейства линий.
> L:=subs(c=2,f1);
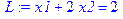
4. Постройте линию уровня, являющейся неявной функцией используя функцию implicitplot, входящуюв библиотекуplots.
Для этого:
-графику первой линии уровня присвойте имя gr;
-построенный график не выводите на экран;
-используйте параметрlinestyle, который используется для указания типа выводимой линии. Тип линии задается следующим образом linestyle=n,где n – целое число, по умолчанию – непрерывная линия при n=1.
> gr:=plots[implicitplot](L,x1=-2..8,x2=-2..8, color=black,thickness=2,linestyle=4):
5. Визуализируйте область допустимых решений syst_ogrи линию уровня grна одном чертеже (рис. 11) при помощи предложения.
> plots[display]({syst_ogr,gr});
Замечание:
Одним из преимуществ системы Maple по сравнению с другими математическими пакетами является возможность помещать в одну область построения разнотипные графики, используя функцию displayбиблиотеки plots.
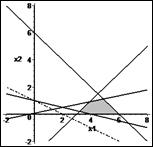
Рис. 11. Область допустимых решений, линия уровня при значении параметра c=2.
6. Очистите значение переменной;
> c:='c':
IV. Нахождение оптимального плана и оптимального значения целевой функции
1. Постройте другие линии уровня при различных параметрах. Выполняйте построение до тех пор, пока не найдется точка на многоугольнике решений, через которую проходит линия уровня функции f с наибольшим (если целевая функция максимизируется) или наименьшим (если она минимизируется) уровнем.
> f1:=x1+2*x2=c;
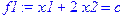
> L:=subs(c=7,f1);
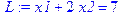
> gr:=plots[implicitplot](L,x1=-2..8,x2=-2..8, color=black,thickness=2,linestyle=4):
> plots[display]({syst_ogr,gr});
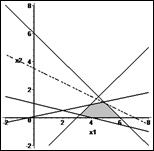
Рис. 12. Область допустимых решений линия уровня при значении параметра c=7.
2. Найдите прямые, пересечение которых соответствует точке выхода.
В данном случае линия уровня достигла наибольшего значения в точке, являющейся пересечением первой и второй прямой.
3. Определите оптимальный план.
Для этого:
-очистите начения переменных x1 и x2;
> x1:='x1':x2:='x2':
-запишите целевую функцию, заданную по условию;
> f:=x1+2*x2;
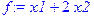
-системе уравнений прямых, пересекающихся в точке оптимума, то есть системе уравнений первой и второй прямой, присвойте имя syst;
> syst:={-3*x1+14*x2=1, x1+x2=6};

-решите эту систему уравнений прямых, а полученное оптимальное решение запишите в переменную optimum.
Замечание:
Для аналитического решения системы алгебраических уравнений в Maple используется команда solve(<система уравнений>, <переменные>). Система уравнений записывается в фигурных скобках, при этом каждое уравнение разделяется запятыми. Результатом решения является множество, каждый элемент которого доступен определенным образом. В нашем случае система уравнений имеет имя syst и две переменных с именами x1, x2. и оптимальное значение целевой функции.
> optimum:=solve(syst,{x1,x2});
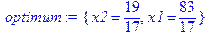
-отделите первую и вторую переменную из множества, используя команду subs.
> x1:=subs(optimum,x1);

> x2:=subs(optimum,x2);
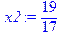
4. Найдите оптимальное значение целевой функции.
> fmax:=subs({x1=83/17,x2=19/17},f);
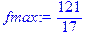
Задания для самостоятельной работы
1. Составьте для нижеприведенных текстовых задач экономико-математическую модель, опираясь на этапы, представленные в Теме 1.
2. Решите каждую задачу геометрическим методом, используя математические пакеты MathCad и Maple, опираясь на материалы лабораторных работ №1 и №2.
3. Сравните полученные ответы.
Задачи о составлении плана производства
Задача 1. Небольшая фабрика изготовляет два вида красок: для внутренних и для наружных работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта – А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 т соответственно. Расходы А и В на 1 т соответствующих красок приведены в таблице.
| Исходный продукт | Расход исходных продуктов (в тоннах) на тонну краски | Максимально возможный запас, т | |
| краска для наружных работ | краска для внутренних работ | ||
| А | |||
| В |
Изучение рынка сбыта показало, что суточный спрос на краску для внутренних работ никогда не превышает спроса на краску для наружных работ более чем на 1 т. Кроме того, установлено, что спрос на краску для внутренних работ никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. долл. для краски для наружных работ, 2 тыс. долл. для краски для внутренних работ. Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Задача 2. Предприятие химической промышленности выпускает соляную и серную кислоту. Выпуск одной тонны соляной кислоты приносит предприятию прибыль в размере 25 ден. ед., выпуск одной тонны серной кислоты – 40 ден. ед. Для выполнения плана необходимо выпустить не менее 200 т соляной кислоты и не менее 100 т серной кислоты. Кроме того, необходимо учитывать, что выпуск кислот связан с образованием опасных отходов. При выпуске одной тонны соляной кислоты образуется 0,5 т опасных отходов, при выпуске одной тонны серной кислоты – 1,2 т опасных отходов. Общее количество опасных отходов не должно превышать 600 т, так как превышение этого ограничения приведет к выплате предприятием крупного штрафа.
Требуется определить, сколько соляной и серной кислоты должно выпустить предприятие, чтобы получить максимальную прибыль. [11]
Задача 3. Предприятие выпускает два вида продукции: А и В. Для производства продукции используется сырье трех типов. На изготовлении изделия А затрачивается 3, 2, 4 единиц сырья каждого типа. На изготовление изделия В затрачивается 2, 3, 3 единиц сырья каждого типа. Предприятие обеспечено сырьем каждого типа в количестве 333, 202, 242 единиц. Прибыль от реализации единицы изделия А и В составляет 25 и 24 денежных единиц соответственно. Определить оптимальный план реализации товаров, обеспечивающих торговому предприятию максимальную прибыль [10].
Задача 4. Один из цехов машиностроительного предприятия выпускает изделия двух видов: корпуса и задвижки. Для производства этих изделий требуются три вида сырья: алюминий, сталь и пластмасса. На выпуск одного корпуса расходуется 20 кг алюминия, 10 кг стали и 5 кг пластмассы. На выпуск одной задвижки расходуется 5 кг алюминия, 5 кг стали и 20 кг пластмассы. Запасы ресурсов ограничены: за рабочую смену цех может израсходовать не более 200 кг алюминия, 250 кг стали и 500 кг пластмассы. Определите количество выпускаемых изделий, при котором прибыль от их производства будет максимальной. Прибыль от выпуска одного корпуса составляет 100 ден. ед., а прибыль от выпуска задвижек составит 300 ден. ед. [11 ]
Задача 5. Для изготовления изделий двух видов имеется 100 кг металла. На изготовление одного изделия вида А расходуется 2 кг металла, а изделия вида В – 4 кг. Составить план производства, обеспечивающий получение наибольшей выручки от продажи изделий, если отпускная стоимость одного изделия вида А составляет 30 руб., а изделия вида В – 20 руб., причем изделий вида А требуется изготовить не более 40, а изделий вида В – не более 20.
Задача 6. Для производства двух видов изделий А и В используется токарное, шлифовальное и фрезерное оборудование. Нормы затрат времени на одно изделие данного вида даны в таблице. В ней же общий фонд рабочего времени каждого из типов оборудования, а также прибыль от реализации 1 изделия.
Найти план выпуска изделий А и В, обеспечивающий максимальную прибыль от их реализации.
| Тип оборудования | Затраты времени на обработку 1 изделия | Общий фонд рабочего времени оборудования | |
| А | В | ||
| фрезерное | |||
| токарное | |||
| шлифовальное | |||
| Прибыль |
[2]
Задача 7.Обработка деталей А и В может производиться на 3 станках, причем каждая деталь при ее изготовлении должна последовательно обрабатываться на каждом из станков. Прибыль реализации детали А составляет 10 единиц, детали В – 16 единиц. Исходные данные указаны в таблице:
| Станки | Норма времени на обработку одной детали | |
| А | В | |
Определить производственную программу, максимизирующую прибыль при условии, что деталей А производится не менее 30 единиц, а деталей В не более 20 единиц. Время работы станков распределено следующим образом: 1 – 100 часов, 2 – 180 часов, 3 – 100 часов.
Задача 8. Хозяйство располагает следующими производственными ресурсами: площадь пашни составляет 600 га, количество человеко-дней машинно-ручного труда 4000. Кроме этого:
| Показатель | Культура | |
| зерновая | кормовая | |
| Затраты труда (человеко-дней) | ||
| Урожайность (ц/га) |
Определить наиболее эффективное сочетание зерновых и кормовых культур при условии, что под кормовые культуры должно быть занято не менее 100 га пашни.
Задачи о пищевом рационе
Задача 1. Стоимость 1 единицы продукта P1 – 2 денежные единицы, продукта P2 – 3 денежные единицы. Требуется так организовать питание, чтобы стоимость его была наименьшей.
| Питательные вещества | Минимальная норма | Содержание питательного вещества в единице продукта | |
| Р1 | Р2 | ||
| белки | |||
| жиры | |||
| углеводы | |||
| Прибыль |
Задача 2.Требуется составить суточный рацион для откорма свиней минимальной себестоимости, причем в рацион должно быть включено не более 2.5 кг ячменя. Минимально потребление кормовых единиц в сутки 2.4 кг, протеина 200 г. Исходные данные приведены в таблице:
| Вид корма | Цена | Содержание питательных веществ | |
| кормовые единицы | протеин | ||
| комбикорм | 1 кг | 100 г | |
| ячмень | 1.2 кг | 80 г |
Дата: 2016-10-02, просмотров: 377.