А. Метод корректировки ставки дисконтирования
Определение рисковой премии, учитываемой при формировании ставки дисконтирования позволяет предотвратить реализацию проектов, общая доходность которых неоправданно завышена. Основным условием при установлении величины рисковой премии является отсутствие учета рисков при формировании исходной экономической информации о проекте, иначе требования к его доходности окажутся завышенными.
Выделяют статистический и экспертный методы обоснования рисковой премии в составе ставки дисконтирования. Выбор метода зависит от того, существует ли статистическая закономерность наступления рискового события.
Статистическим методом оценивают риски, связанные с надежностью работы оборудования, качеством выпускаемой продукции, поскольку возможно получение информации о вероятности отказов оборудования, аварий, браке и других потерях. Статистические закономерности можно установить по природным рискам, связанным со стихийными бедствиями, авариями.
Использование статистического метода оценки риска возможно на основе поэлементного или агрегированного подходов. Поэлементный подход предполагает учет каждого вида риска в отдельности: определяется номенклатура рисков, подлежащих отражению в ставке дисконтирования, оценивается влияние каждого из них на величину рисковой премии. С помощью агрегированного подхода рисковая премия оценивается укрупненно по всем видам рисков.
При использовании «бета-анализа» требуемая доходность проекта может быть рассчитана по формуле CAPM:
Ri = Rб + (IRRmid – Rб ) * b где
Ri – требуемая с учетом риска норма доходности проекта;
Rб – норма дохода по безрисковым инвестициям;
IRRmid – средняя норма дохода на инвестиционном рынке (аналогичных проектов);
b - коэффициент систематического риска, рассчитываемый по результатам рыночных наблюдений.
Используя значения b-коэффициента, можно оценивать уровень риска всей инвестиционной программы предприятия (табл. 7). b инвестиционной программы равен средневзвешенной b-коэффициентов отдельных инвестиционных проектов.
Таблица 7
Использование b-коэффициента для оценки уровня риска
| Значения b-коэффициента | Уровень риска |
| b = 1 | средний |
| b > 0 | высокий |
| b < 0 | низкий |
Следовательно, величину риска инвестиционной программы можно уменьшить, изменяя набор проектов в ней, т.е. выбирая проекты с разным удельным весом инвестиций в общей программе.
В рамках статистического метода определения рисковой премии можно выделить еще два подхода, которые теоретически могут иметь место.
В качестве показателя, определяющего величину рисковой премии, может выступать среднее квадратичное отклонение IRR. Использование для оценки риска проекта метода сценариев позволяет оценить вероятности достижения проектом различных значений внутренней нормы доходности и определить среднее значение его доходности. Тогда на основании математических законов можно утверждать, что если распределение является непрерывным и близким к нормальному, то 68,3% всех возможных значений IRR лежит в пределах одного среднего квадратического отклонения от ожидаемого значения, 99,5% значений IRR – в пределах двух средних квадратических отклонений. Поэтому величину среднего квадратичного отклонения целесообразно использовать в качестве рисковой премии.
Недостаток статистического метода оценки риска заключается в необходимости большого массива исходных данных для расчета, который трудно получить, поэтому на практике при оценке рисковой премии часто используют экспертный метод.
Величину платы за риск можно устанавливать и на основе экспертного метода. Содержание экспертного метода состоит в обработке мнений специалистов о величине рисковой премии в целом по проекту или по отдельным наиболее вероятным с их точки зрения видам рисков. Возможно использование экспертного метода при поэлементном расчете рисковой премии (по видам рисков). Одна из классификаций факторов и размеров рисковой премии приведена в табл. 8.
Таблица 8
Установление рисковой премии в зависимости от вида и фактора риска
| Факторы и виды риска | Прирост премии за риск, % |
| 1. Необходимость проведения НИОКР (с заранее неизвестными результатами) силами специализированных научно-исследовательских и (или) проектных организаций: | |
| · продолжительность НИОКР менее 1 года | 3-6 |
| · продолжительность НИОКР свыше 1 года: | |
| Ø НИОКР выполняется силами одной специализированной организации | 7-15 |
| Ø НИОКР имеет комплексный характер и выполняется силами нескольких специализированных организаций | 11-20 |
| 2. Характеристика применяемой технологии | |
| · традиционная | |
| · новая, требующая применения ресурсов, имеющихся на свободном рынке | 2-4 |
| · новая, требующая в отличие от существующей применения монополизированных ресурсов | 5-10 |
| · новая, исключающая в отличие от существующей применение монополизированных ресурсов | 1-3 |
| 3. Неопределенность объемов спроса и цен на производимую продукцию: | |
| · существующую | 0-5 |
| · новую | 5-10 |
| 4. Нестабильность (цикличность) спроса на продукцию | 0-3 |
| 5. Неопределенность внешней среды при реализации проекта: горно-геологические, климатические и иные природные условия, агрессивность внешней среды и т.п. | 0-5 |
| 6. Неопределенность процесса освоения применяемой техники и технологии | 0-3 |
Экспертный метод широко используют для определения агрегированной рисковой премии без разделения ее по видам рисков. При этом необходимо учитывать целевую направленность инвестиций, новизну и сложность применяемого оборудования. Для установления предельного размера рисковой премии можно воспользоваться материалами исследования ряда американских компаний, дифференцирующих норму дохода в зависимости от класса инвестиций.
Учитывая, что уровень безрисковой доходности составляет примерно 5% (ориентир – доходность государственных облигаций РФ), можно определить размер рисковой премии по перечисленным классам инвестиций, вычитая из соответствующей нормы дохода величину безрисковой составляющей (табл. 9)
Таблица 9
Установление рисковой премии в зависимости от класса инвестиций
| Класс инвестиций | Норма доходности, % | Размер рисковой премии, % |
| 1. Вложения с целью сохранения позиций на рынке (повышение качества продукции, реклама) | ||
| 2. Инвестиции на обновление основных фондов | ||
| 3. Инвестиции с целью экономии текущих затрат (на базе новых технологических решений) | ||
| 4. Вложения с целью увеличения доходов (для проектов, направленных на расширение производства на новой технологической основе на стабильном рынке) | ||
| 5. Венчурные инвестиции (в инновационные проекты) |
Недостаток экспертного метода – субъективность, связанная с влиянием на оценку индивидуальных особенностей эксперта.
Таким образом, метод корректировки дисконта имеет ряд недостатков, которые препятствуют его использованию в качестве единственного метода оценки риска инвестиций и принятия инвестиционных решений. Тем не менее, корректировка стоимости капитала как метод расчета дисконта, остается необходимым приемом, применяемым в ходе оценки эффективности инвестиций с целью учета полных экономических издержек привлечения капитала. При этой корректировке может использоваться показатель систематического риска, если капитал привлекается на рынке и портфель компании достаточно диверсифицирован, или общий риск, когда нарушаются данные условия и стоимость капитала существенно зависит от общего риска. Учет зависимости ставки дисконтирования от риска является необходимым условием достоверной оценки чистой текущей стоимости инвестиций. В то же время риск проектов должен быть оценен иным методом и отражен в отдельном показателе, например в стандартном отклонении.
Б. Метод достоверных эквивалентов
Метод достоверных эквивалентов предполагает корректировку денежных потоков инвестиций в зависимости от достоверности оценки их ожидаемой величины. Данный метод известен в нескольких вариантах и получил распространение благодаря своей простоте. Наиболее распространенный вариант — экспертная корректировка денежных потоков на понижающий коэффициент в зависимости от субъективной оценки вероятностей. Однако интерпретация коэффициентов достоверности как вероятностей, свойственная данному подходу, не соответствует экономической сущности оценки риска. Если денежный поток ожидается равным определенному значению с данной вероятностью (например, 100 тыс. руб. с вероятностью 0,20), то понижение чистой текущей стоимости проекта на данный коэффициент (0,20) никак не соотносится с рисковыми предпочтениями инвестора. Применение коэффициентов достоверности в такой трактовке делает принятие инвестиционных решений произвольным и при формальном подходе может привести к серьезным ошибкам в управлении.
Другая интерпретация метода связывает коэффициенты достоверности с абсолютно достоверными доходами — по безрисковым вложениям. Применение таких коэффициентов сводит денежные потоки к поступлениям от безрисковых активов, что лишает смысла весь анализ инвестиций. Данный вариант метода абсолютно неработоспособен, хотя исходная информация для его применения легко доступна на практике.
Единственное теоретически верное применение метод достоверных эквивалентов находит в методе предпочтительного состояния, который является обобщением метода чистой текущей стоимости для состояния неопределенности. Метод предпочтительного состояния состоит в явном учете всех альтернативных вариантов событий (фактически, в построении «дерева решений»), для каждого из которых используется свой коэффициент дисконтирования с поправкой на риск (RPVF). Коэффициенты дисконтирования с поправкой на риск отражают рыночную стоимость инвестиций и соответствуют доходности хеджированного портфеля, эквивалентного данной инвестиции. Они могут быть определены следующим образом:
RPVF(A)=P(A)*PVF*Kr, где
Р(А) — вероятность наступления состояния A;
PVF — коэффициент дисконтирования по безрисковой ставке;
Кr - коэффициент поправки на риск, отражающий предпочтение ликвидности инвестора в состоянии А.
Множитель Р(А)*Кr является достоверным эквивалентом. Он отражает рыночную оценку вероятности данного состояния экономики и относительной ценности денег для инвесторов (индекс Кr) в этом состоянии. Сумма достоверных эквивалентов, как и сумма вероятностей, должна равняться 1, поскольку они соответствуют текущей рыночной стоимости активов, приносящих доход в 1 руб. в данном состоянии экономики, а портфель, сформированный из таких активов, является безрисковым. В этом случае достоверные эквиваленты используются для приведения к текущей стоимости денежных потоков, которые дает инвестиция в различных состояниях экономики. Метод дает инвестициям комплексную рыночную оценку и должен применяться на предприятиях с соответствующими ограничениями (на общий риск портфеля). Недостатком метода является сложность определения достоверных эквивалентов и коэффициентов дисконтирования с поправкой на риск.
Таким образом, неоспоримым достоинством рассмотренных методов является то, что они позволяют связать оценку риска с оценкой эффективности инвестиций. Однако применение обоих методов связано с использованием показателя оценки риска инвестиционного проекта как некоего заданного параметра. Поэтому их применение возможно только после получения такого показателя путем использования других методов количественной оценки риска.
2.Методанализа чувствительности
Метод анализа чувствительности критериев эффективности инвестиций дает финансовым аналитикам возможность объективно и на количественной основе оценить влияние на проект изменения его ключевых переменных. Метод состоит в элиминировании влияния каждого фактора модели денежных потоков и чистой текущей стоимости (или другого критерия) и оценке реакции результативного показателя (NPV, IRR, DPB) на изменение ключевых переменных (объема реализации, цен на продукцию и производственные ресурсы, стоимости капитала). То есть, этот метод показывает, насколько изменятся NPV и IRR в ответ на данное изменение одной входной переменной при условии, что все остальные факторы не меняются.
Анализ чувствительности начинается с детального изучения и описания факторов, которые не могут быть изменены посредством управленческих решений, т.е. относящихся к внешней среде предприятия. Детальное изучение показателей внешней среды необходимо для достоверного прогноза их развития и построения возможных вариантов реализации инвестиционного проекта. Следует также определить степень предполагаемого изменения варьируемых показателей и влияния их друг на друга.
Для проведения анализа чувствительности необходимо разработать план.. В практической деятельности принят стандартный минимальный набор показателей, влияние которых встречается чаще других табл.10). Последовательно изменяя значение входных переменных в равной (в процентах) степени по отношению к их базисному значению, рассчитывают показатель эффективности проекта. Результаты удобно систематизировать в табличной форме, которая наглядно покажет, изменение каких входных переменных вызывает наиболее значительное изменение показателя эффективности.
Таблица 10
Изучаемые факторы, влияющие на эффективность проектов
| № п/п | Перечень варьируемых параметров проекта |
| Физический объем продаж | |
| Цена на продукцию при неизменном объеме продаж | |
| Прямые (переменные) производственные издержки | |
| Постоянные (накладные) производственные издержки | |
| Длительность инвестиционного периода | |
| Сумма инвестиционных затрат | |
| Время задержки платежей за продукцию | |
| Изменение ставки кредитования | |
| Сокращение срока возврата кредита |
Следующим шагом в анализе чувствительности является расчет показателей эффективности по исходной информации, учитывающей изменение варьируемых параметров. Использование ЭВМ существенно упрощает эти расчеты. (анализ чувствительности можно реализовать, как с помощью специальных программных пакетов типа Project Expert, так и программы Excel.)
Для удобства все рассчитанные показатели сводятся в таблицу следующего вида (табл. 11).
Таблица 11
Оформление результатов анализа чувствительности
| № п/п | Вариант расчетов | Показатель эффективности | |
| 1. | Базисные значения всех входных переменных | NPV o | |
| 2. | Изменение объема продаж | NPV 1 | |
| 3. | Изменение цены продаж | NPV 2 | |
| 4. | Изменение срока службы оборудования | NPV 3 | |
| И т.д. |
Сопоставление результатов оценки эффективности базового варианта и рассчитанных сценариев позволит оценить степень устойчивости проекта к различным видам риска.
Анализ чувствительности позволяет также наглядно представить зависимость показателей эффективности проекта от варьируемых параметров. Так, на рис. 9 показаны графики чувствительности NPV некоторого условного проекта для трех входных переменных.
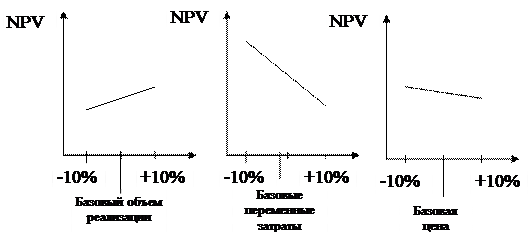 |
Рис. 9. Кривые чувствительности NPV к изменению входных переменных.
Наклон линий регрессии показывает, насколько чувствителен NPV проекта к изменениям на каждом входе: чем круче наклон, тем чувствительнее NPV к изменению переменной. На рис.9 видно, что показатель NPV проекта очень чувствителен к изменению перемененных затрат, довольно чувствителен к изменениям объема сбыта и относительно нечувствителен к изменению цены капитала. То есть анализ чувствительности позволяет выявить те виды риска, которые могут оказать наибольшее влияние на проект. Ранжирование параметров позволяет более эффективно управлять инвестиционными рисками.
В сравнительном анализе, проект с более крутыми кривыми чувствительности считается более рисковым, поскольку сравнительно небольшая ошибка в оценке переменной, дает в этом случае большую ошибку в прогнозируемой NPV проекта. Таким образом, анализ чувствительности позволяет проникнуть в суть рискованности проекта.
Анализ чувствительности очень нагляден, однако главным его недостатком является то, что анализируется влияние только одного из факторов, а остальные считаются неизменными. На практике же обычно изменяются сразу несколько показателей. Оценить подобную ситуацию и скорректировать NPV проекта на величину риска помогает сценарный анализ. Поэтому анализ чувствительности часто используют в рамках других методов оценки риска (имитационное моделирование, метод сценариев) для выявления ключевых факторов, оказывающих влияние на проект.
Кроме того, анализ чувствительности позволяет определить предельные значения параметров проекта, за которыми проект становится неэффективен. На графике это точка пересечения кривыми зависимости оси абсцисс.
3. Методы, позволяющие оценить форму распределения вероятностей (профиль риска)
Методы анализа риска инвестиционного проекта, предполагающие построение кривых распределения вероятностей (профилей риска), сопряжены с большими трудозатратами, но являются наиболее информативными из всех методов анализа рисков. В финансово-инвестиционном анализе применяются метод сценариев, «построение деревьев решений» и приемы имитационного моделирования.
А. Метод построения «дерева решений»
Метод построения «дерева решений» основан на построении многовариантного прогноза динамики внешней среды. В отличие от метода сценариев (см. ниже), он предполагает возможность принятия самой организацией решений, изменяющих ход реализации проекта (осуществление выбора) и особую графическую форму представления результатов («дерево решений»). «Дерево решений» может применяться как в условиях риска, так и в условиях неопределенности или полной определенности. Аналитик подсчитывает значения выбранного критерия эффективности (например, NPV) вдоль каждой «ветви» дерева, а при анализе рисков — также и вероятность каждого значения. На основе полученных значений можно построить кривую распределения вероятностей (профиль риска) и выбрать оптимальный вариант реализации проекта. Преимуществом «дерева решений» является наглядность результатов и процесса анализа, а недостатком — его техническая сложность при больших размерах «дерева».
Б. Имитационное моделирование
Имитационное моделирование инвестиционных процессов является наиболее мощным и технически сложным инструментом анализа инвестиционного риска и требует использования соответствующего программного обеспечения. Метод имитационного моделирования состоит из этапов выявления детерминированных и стохастических зависимостей внутренних переменных проекта и переменных внешней среды, построения модели, проведения симуляции путем случайной вариации ключевых переменных, построения кривых распределения вероятности и расчета показателей уровня риска на основе результатов симуляции. Метод дает наиболее точные и обоснованные оценки вероятностей при наименьших трудозатратах по сравнению с прочими методами, однако точность оценок в значительной степени зависит от качества исходных предположений и учета взаимосвязей переменных внешней среды. Современные программные средства позволяют учесть форму распределения вероятности и корреляции десятков внешних переменных, однако оценить эти значения в практическом исследовании обычно не представляется возможным. Инвестиционные аналитики измеряют вариации основных переменных макро- и микросреды, оценивая разброс значений второстепенных переменных и статистические связи между факторами экспертным путем. Поэтому возможности имитационных моделей обычно не бывают полностью задействованы.
В. Метод сценариев
Метод сценариев предполагает прогнозирование вариантов развития внешней среды и расчет оценок эффективности инвестиций для каждого сценария. Если сценариям приписываются определенные вероятности, то можно построить профиль риска, оценить стандартное отклонение и асимметрию распределения. Часто разрабатывают так называемые «пессимистический», «наиболее вероятный» и «оптимистический» сценарии, позволяющие приближенно оценить разброс результатов проекта и его прибыльность (убыточность) при ухудшении экономической ситуации.
В сценарном анализе при определении ключевых факторов проекта используют результаты анализа его чувствительности.
При этом предлагается применять анализ чувствительности по всем факторам (цена реализации, рекламный бюджет, объём продаж, себестоимость продукции и т. д.), используя специализированные пакеты типа Project Expert, что позволит существенно сократить время расчётов.
Анализ сценариев предполагает расчет NPV по каждому из возможных вариантов (наилучшему, наихудшему, наиболее вероятному). В результате получается массив значений NPV (табл. 12) .
Таблица 12
Массив значений NPV
| Сценарий | … | n | |||||
| Вероятность | Р1 | Р2 | Р3 | Р4 | Р5 | … | Рn |
| NPV | npv1 | npv2 | npv3 | npv4 | npv5 | … | npvn |
Далее представляется возможность рассчитать ожидаемое значение NPV, среднее квадратичное отклонение и коэффициент вариации.
Ожидаемое значение NPV рассчитывается по формуле математического ожидания, т.е. М (NPV) = å NPVi*Pi,
Среднее квадратичное отклонение определяется, как было уже показано ранее как
σnpv = [(ki – M(k))2*Pi ] 1\2.
А коэффициент вариации как отношение среднего квадратичного отклонения к величине матожидания:
К вар = σnpv / М (NPV).
Полученный результат используют для сравнения уровня риска альтернативных проектов: чем выше коэффициент вариации, тем и выше риск. При отборе проектов могут использовать предельные значения коэффициента вариации, тогда проекты с превышающими данный предел коэффициентами отклоняют.
В случае отсутствия информации о вероятности сценариев для расчета ожидаемого значения показателя эффективности можно использовать формулу:
NPVож = NPVmax + (1 - l)NPVmin где
l - специальный норматив для учета неопределенности эффекта, отражающий систему предпочтений соответствующего участника проекта в условиях неопределенности. На практике рекомендуется применять коэффициент в размере 0,3;
NPVmax, NPVmin – наибольший и наименьший NPV по рассмотренным сценариям.
Таким образом, метод анализа сценариев позволяет получать достаточно наглядную картину для различных вариантов реализации проектов, а также предоставляет информацию о чувствительности и возможных отклонениях.
К недостаткам метода сценариев, как правило, относят то, что ограничивается рассмотрение только нескольких дискретных исходов проекта, в то время как в действительности существует очень большое число возможностей. Однако, применение программных средств, даже типа Excel позволяет значительно повысить эффективность сценарного анализа путем практически неограниченного увеличения числа сценариев и введения дополнительных переменных.
Если существует множество сценариев развития ситуации, но их вероятности не могут быть оценены, то для выбора инвестиций применяются методы теории игр (критерий максимина, «игра с природой» и др.). Хотя методы теории игр позволяют найти наиболее «безопасное» решение, его принятие значительно снижает доходность инвестиций. Поэтому экономические субъекты предпочитают находить баланс доходности и риска в зависимости от своих рисковых предпочтений. Для этого принимаются меры по снижению неопределенности (получению дополнительной информации). Дополнительная информация может быть получена путем изучения рынка, осуществления пробных капиталовложений и т.п.
Таким образом, анализ рисков инвестиционного проекта позволяет:
1. выявить все возможные риски проекта
2. упорядочить риски на основании избранной классификации, получив наглядную систему рисков проекта
3. выявить риски, способные оказать наибольшее влияние на проект
4. рассчитать количественные показатели риска
5. рассчитать важнейшие показатели эффективности проекта с учетом фактора риска
6. создать основу для выработки мер воздействия на риски
7. выработать убедительные аргументы при заключении договоров на финансирование проекта, т.е. установить точку опоры в конфликте интересов инвестора и остальных участников проекта.
Дата: 2016-09-30, просмотров: 338.