В данной работе рассматривается работа с русской версией среды GeoGebra.
При запуске окно программы имеет вид, приведенный на рис. 7
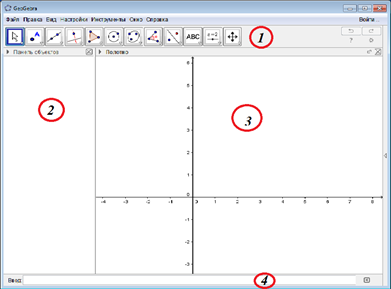
Рис. 7
В отличии от других программ в окне программы находится Панель инструментов(1), Панель объектов(2), Место геометрических построений(3) и Строка ввода(4). Чтобы перейти в полотно 3D необходимо в строке меню нажать в кладку Вид (Рис. 8).
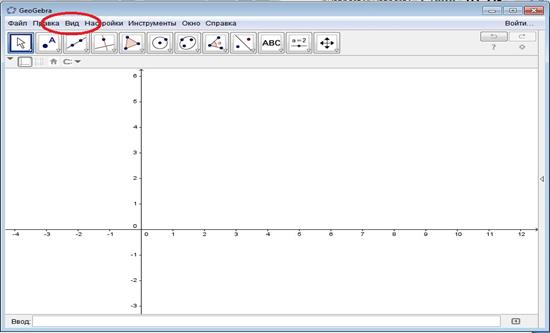
Рис. 8
При нажатии на вкладку Полотно 3D GeoGebra переходит в 3D конструктор (Рис. 9а и 9б).
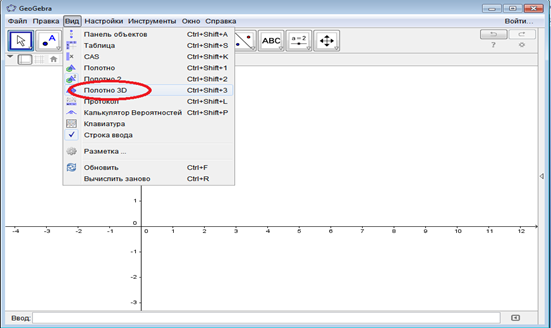
Рис. 9а
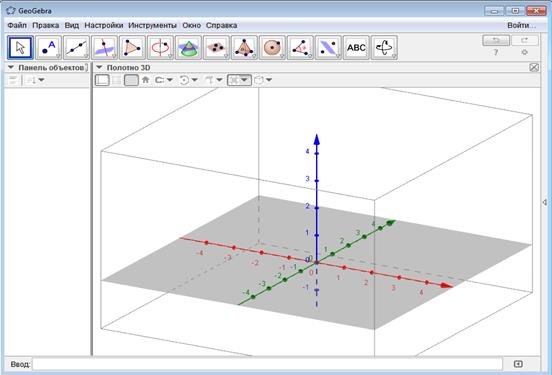
Рис. 9б
Расположение свободных объектов возможно менять как угодно, а зависимые могут меняться только с учетом свободных.
В строку ввода входят две части: это естественно Строка ввода, и Список команд, где есть список команд для ввода. Также можно отключить Отображение Списка команд, перейдя в меню Вид.
Отображение Панели объектов и Строки ввода можно выключить в меню Вид. Здесь же возможно включить отображение другого элемента окна программы – Таблицы и одного типа объектов - вспомогательных.
Рассмотрим обучение геометрии с использованием программы «GeoGebra».
При открытии программы GeoGebra на месте геометрических построений находятся координатные оси. При необходимости можно сделать прорисовку координатной сетки с помощью команды Вид - Сетка. Если необходима подробная настройка рабочего места, то следует выполнить команду Настройки - Полотно.
На вкладках Оси и Сетка можно изменить цвет объектов, способы начертания. Для осей возможно указать их обозначение, единиц измерения и т.д.
Разнообразные инструменты для геометрических построений находятся на Панели инструментов. Они разделены на группы, которые скрыты в маленьком треугольнике в нижнем правом углу. Если на него нажать, то раскроется меню, в котором можно выбрать нужный инструмент. При построении геометрических объектов на Панели объектов вся информация вносится автоматически, а объекты выводятся в Области геометрических построений.
Все объекты делятся на свободные и зависимые. К свободным входят все независимые объекты, что значит построенные произвольно в области построений. Зависимые объекты строятся, исходя из имеющихся свободных или зависимых объектов.

Рис. 10
С целью построения разных объектов применяется Панель инструментов, инструменты в которой разбиты в категории. Рассмотрим поочередно существующие в распоряжении пользователя приборы (Рис. 10).
С помощью инструмента Перемещать (Рис.11) можно менять положение объектов на координатной плоскости. Чтобы выделить сразу пару объектов, необходимо не отпуская клавиши Ctrl последовательно указать на них мышью.

Рис. 11
Для того, чтобы построить точку необходимо воспользоваться инструментом Точка (Рис. 12), и указать расположение на плоскости. Она задается парой координат и обозначается заглавной буквой латинского алфавита. Если навести курсор на область построений, то он примет вид крестика, рядом с ним выводятся текущие координаты. Точка имеет синий цвет.
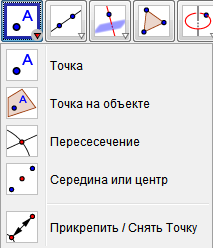
Рис.12
Чтобы построить точку на объекте нужно воспользоваться функцией Точка на объекте (Рис. 12). Когда выбираем этот элемент, необходимо учитывать, что её можно ставить только на объекте, так как не сможет покинуть объекты границы. Зато перемещать точку внутри объекта можно. Эта точка тоже имеет синий цвет.
Для того, чтобы построить точки, которые являются пересечение двух объектов необходимо воспользоваться инструментом Пересечение двух объектов (Рис. 12). После этого нужно выбрать эти два объекта, точки пересечения которых нужно было построить. Они будут иметь серый цвет и являться зависимыми объектами. При построении середины отрезка необходимо воспользоваться инструментом Середина или центр (Рис. 12). Далее показать концы отрезка двумя точками или отрезок, середину которого нужно построить. С помощью этого же инструмента можно построить центр геометрической фигуры.
Чтобы прикрепить или снять прикрепленную точку есть функция Прикрепить/Снять точку (Рис. 12).
Функция Комплексное число (Рис. 12) дает возможность вставить точку на нужную плоскость. Точка окрашивается в синий цвет. Инструменты Прямая по двум точкам, Отрезок по двум точкам, Луч по двум точкам, Вектор по двум точкам (Рис.13) строят прямую, отрезок, луч и вектор соответственно по указанию на две точки, через которые проходит нужная линия. Можно выбирать точки, которые уже имеются на чертеже, или показывать мышью, где будут находиться эти точки.
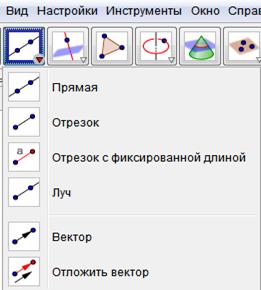
Рис. 13
Чтобы построить прямую перпендикулярную данной, необходимо воспользоваться инструментом Перпендикулярная прямая (Рис. 14), далее показать прямую, к которой будет построена перпендикулярная. И конечно точку, через которую будет проходить прямая. Точно так же строится прямая, параллельная данной, с помощью инструмента Параллельная прямая.
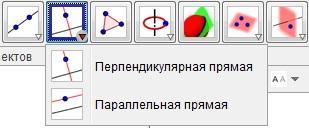
Рис. 14
Для того, чтобы построить произвольный многоугольник нужно использовать инструмент Многоугольник (Рис. 15). Чтобы построить фигуру с его помощью нужно последовательно указать все вершины многоугольника, а дальше указать на вершину, откуда начиналось построение.
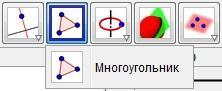
Рис. 15
Есть несколько вариантов, чтобы построить окружность. Первая функция Окружность по точке и оси (Рис. 16) дает возможность построить окружность в нужной оси, но с неизвестным радиус, то есть произвольную окружность. Вторая функция данной подгруппы — это Окружность с центром, радиусом и направлением (Рис. 16) дает возможность построения окружность с фиксированным центром, направлением и с заданным центром. Чтобы использовать эту функцию необходимо мышкой показать, в каком месте находится центр, далее направление радиуса и под конец вести размер радиуса. Последняя функция данной подгруппы дает возможность построения окружности по трем точкам на любой поверхности оси. Эта функция называется Окружность по трем точкам (Рис. 16).

Рис. 16
Данная подгруппа функций позволяет построить плоскости. Функция Плоскость через три точки (Рис. 17) дает возможность построить плоскость на любой оси через любые три точки. Плоскость имеет серый цвет. Plane (Рис. 17).
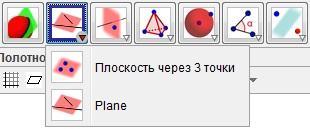
Рис. 17
Перпендикулярная плоскость, Параллельная плоскость. Эти функции дают возможность построить плоскости перпендикулярные и параллельные соответственно. Для того, чтобы построить перпендикулярную плоскость выбирается точка мышью и перпендикулярная прямая к данной точки. Плоскость строится автоматически. Для построения параллельной плоскости выбирается точка и параллельная плоскость, остальные действия аналогичны построению перпендикулярной плоскости (Рис. 18).
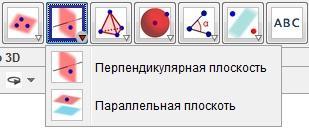
Рис. 18
Главными фигурами в геометрии считаются пирамида и призма, именно поэтому данная подгруппа функций для этих фигур. Функции Пирамида и Призма дают возможность построить данные фигуры через любые точки и в любой плоскости оси координат (Рис. 19).
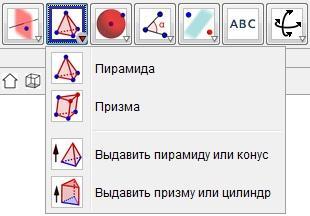
Рис. 19
С помощью функций Выдавить пирамиду или конус и Выдавить призму или цилиндр (Рис. 19) возможности построения увеличиваются в двойне.
Последняя подгруппа функций, которую хочу представить это функции Сфера по точке и центру, Сфера по центру и радиусу, Cone и Cylinder (Рис. 20). Как видно по названиям эта подгруппа специализируется построению сферических фигур. [21, с. 36]
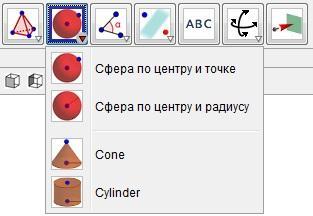
Рис. 20
Рассмотрев все основные элементы для построения, теперь попробуем решить задачу и построение в GeoGebrе:
Дана прямая а, две точки А и В лежат в одной полуплоскости от этой прямой. Требуется найти такую точку С, которая должна лежать на прямой а, и такая должна быть, чтобы АС+ВС принимала бы самое маленькое значение, наименьшее значение из всех других точек, которые лежат на этой прямой.
АА1^а; АМ=А1М
А1В=А1С+СВ=АС+СВ
АХ+ХВ= А1Х+ХВ
А1В<А1Х+ХВ.
АС+СВ<АХ+ХВ
Есть точка А и есть точка В. Возьмем точку А1, симметричную точке А относительно прямой а. Это значит, АА1^а и, если здесь есть точка М, АМ=А1М. Во – первых, перпендикуляр, и, во – вторых, равенство вот этих отрезков.
Берем точку В1, симметричную точке В. То же самое: это равно этому, эти длины равны. Это на самом деле брать необязательно. Важно, что одну точку мы нашли – А1, которая симметрична точке А. Этого достаточно. И соединим точку В и точку А1. Оказывается, получим искомую точку С. (Рис. 21) Осталось только доказать, что именно она – искомая, а не какая – нибудь другая.
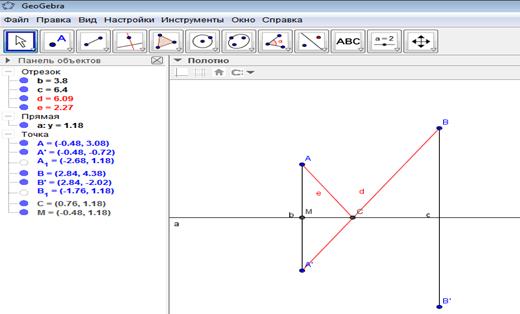
Рис. 21
Мы утверждаем, что сумма этих длин АС+СВ будет меньше, чем длина АХ+ХВ. Почему? В силу симметрии мы утверждаем, что А1В=А1С+СВ. Отрезок А1С=АС – это легко доказать, что этот отрезок равен этому отрезку. Значит, А1В=А1С+СВ=АС+СВ.
Итак, длина вот этой ломаной равна длине отрезка, длине прямолинейного отрезка. А длина второй ломанной? АХ+ХВ= А1Х+ХВ. Учтем, что АХ=А1Х, т.е. длина этой ломаной равна длине вот этой ломаной. Но в силу неравенства треугольника А1В<А1Х+ХВ. Значит, АС+СВ<АХ+ХВ. Причем это для любой другой точки Х на прямой, не совпадающей с точкой С. Итак, задача заключалась в следующем: надо было на прямой а найти такую точку С, сумма расстояний от которой до точек А и В была бы самой наименьшей из всех других точек прямой а. Решение: взяли точку симметричную, получили точку А1. Соединили, на пересечении с прямой а получили искомую точку С. Почему эта точка именно искомая? Потому что длина А1В<А1Х+ХВ, т.е. АС<СВ. Это одна из задач на построение.
Заключение
Систематическое изучение геометрических построений необходимо в школьном курсе, так как в процессе изучения задач они концентрируют в себе знания из других областей математики, развивают навыки практической графики, формируют поисковые навыки решения практических проблем, приобщают к посильным самостоятельным исследованиям, способствуют выработке конкретных геометрических представлений, а также к более тщательной обработке умений и навыков.
В работе рассмотрены:
1. Методы решения задач на построение по геометрии:
• метод геометрических мест;
• методы геометрических преобразований;
• метод симметрии;
• метод параллельного переноса;
• метод поворота;
• метод подобия;
• алгебраический метод;
2. Методика решения задач на построение по геометрии:
• анализ;
• построение;
• доказательство;
• исследование.
Цель исследования – изучить методику решения задач на построение в школьном курсе геометрии была достигнута.
В соответствии с проблемой, объектом, целью были реализованы следующие задачи исследования:
1. Проведен анализ школьных учебников по геометрии разных авторов;
2. Рассмотрены главные этапы решения задач на построение;
3. Рассмотрены методы решения задач на построение;
4. Осуществлено ознакомление с компьютерной программой GeoGebra.
При написании курсовой работы по теме исследования была изучена литература, включающая научные статьи, учебники по математике, рассмотрено практическое применение задач на построение в школьном курсе по геометрии.
Таким образом, необходимо уделять больше внимания изучению задач на построение, так как при грамотном использовании они являются мощным средством развития логического мышления учащихся; геометрические задачи на построение не нужно рассматривать как что – то отдельное, независимое от остального курса геометрии. Процессы обучения решению задач и изучение геометрии неразрывно связаны. Причем связь эта должна быть двусторонней, то есть необходимо не только обучать решению задач на построение, используя ранее полученные знания, но и, наоборот, использовать конструктивные задачи при изучении геометрии.
Список литературы
1. Александров, И.И. Сборник геометрических задач на построение с решениями / И.И.Александров. – М.: Учпедгиз,1994.
2. Аргунов, Б.И. Элементарная геометрия: учеб. пособие для пед. ин-тов / Б.И. Аргунов, М.Б. Балк. – М.: Просвещение, 2008.
3. Белошистая, А.В. Задачи на построение в школьном курсе геометрии / А. В. Белошистая // Математика в школе. – 2011. – №9. – С. 47-50.
4. Геометрия: учеб. для 7-9 кл. общеобразовательных учреждений / А. В. Погорелов. – М.: Просвещение, 2012.
5. Геометрия: учеб. для 7-9 кл. сред. шк. / А. Д. Александров, А. Л. Вернер, В.И. Рыжик. – М.: Просвещение, 2012.
6. Геометрия: учеб. для 7-9 кл. сред. шк / Л. С. Атанасян. – М.: Просвещение, 2012.
7. Геометрия: Планиметрия: 7-9 кл.: учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 2005.
8. Иванчук Н.В., Эйкен О.В., Мартынова Е.В. Использование программы GeoGebra на уроках математики в 7-11 классах: Методическое пособие. – Мурманск: МГПУ, 2008.– 36 с.
9. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ВятГГУ, 2008. – С. 59-69.
10.Мисюркеев, И.В. Геометрические построения. Пособие для учителей / И.В.Мисюркеев. – М: Учпедгиз, 1950.
11.Общая психология: учеб. для студентов пед. ин-тов / под ред. А. В. Петровского. – М.: Просвещение, 1986.
12.Прасолов, В.В. Задачи по планиметрии. Ч.1 / В.В. Прасолов. – М.: Наука, 1991.
13.Прасолов, В.В. Задачи по планиметрии. Ч.2 / В.В. Прасолов. – М.: Наука, 1991.
14.Шарыгин, И.Ф. Задачи по геометрии (Планиметрия) / И.Ф. Шарыгин. – М.: Наука, 2009.
Дата: 2019-11-01, просмотров: 493.