Зачастую построение фигуры делается трудным только лишь потому, что части данной фигуры очень далеки друг от друга, и по этой причине сложно внедрить в чертёж сведения. В таких ситуациях ту или иную часть искомой фигуры переносят либо параллельно себе, либо иным способом, однако на такой промежуток, чтобы снова начерченная фигура имела возможность на построение. Направление подобного перенесения находится в зависимости с требование задачи и обязано подбираться таким образом, чтобы в снова построенную фигуру вошло наибольшее число сведений.

Пример 6:

 Построить трапецию по заданным сторонам. [19, с. 200]

Решение. Анализ. Пусть трапеция АВС D построена, ВС= а, А D = b , AB = c, CD = d (рис. 4)

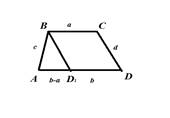
Рис.4

Начертим параллельный перенос, определяемый вектором СВ. Тогда сторона С D перейдёт в BD 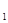. Треугольник АВ D  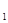можно построить по трём сторонам c , d , b - a ( b > a ).

Далее продолжим отрезок 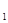А D  на D 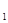D = a. Через точку В проведем прямую, параллельную А D и на ней отложим отрезок ВС= а. Соединим точки С и D. Полученная трапеция АВС D – искомая.

План построения очевиден.

Доказательство. В четырехугольнике АВС D BC параллельна AD, значит ABCD – трапеция в которой AB = c , AD = b, так как AD = b – a + a . BD = CD = d .

Исследование. Треугольник ABD  можно построить по трём сторонам, если c – d < b – a < c + d. При этом условии однозначно выполнимы и все остальные шаги построения. Если же неравенство c – d < b – a < c + d не выполняется, то задача не имеет решения.

Метод поворота

Метод поворота при в решении задач на построения состоит в том, что отдельные элементы фигуры поворачиваются с целью получения новой фигуры, построение которой известно. Приведем пример, иллюстрирующий применение этого метода.

Пример 7:

Даны три параллельные прямые a, b и с. Построить равносторонний треугольник АВС, вершины А, В, С которого лежат на данных прямых.

Решение.

    Анализ. Предположим, что задача решена и D АВС – искомый (рис.5).

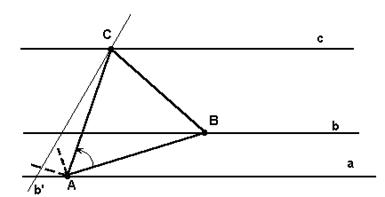
Рис. 5

Так как АВ=АС и Ð ВАС=60⁰, то точка В переходит в точку С при повороте вокруг точки А на угол 60⁰ или на угол –60⁰ (ибо Ð ВАС=+60⁰ или –60⁰). Пусть, например, точка В переходит в точку С при повороте вокруг точки А на угол +60⁰. Точка В лежит на прямой b. Поэтому точка С, получающаяся из нее поворотом вокруг точки А на угол +60⁰ должна лежать на прямой b ¢ , получающейся из прямой b поворотом вокруг точки А на угол +60⁰. Кроме того, точка С лежит, по условию, на прямой с. Поэтому точка С есть точка пересечения прямых b ¢ и с.

Аналогично, если точка В переходит в точку С при повороте на угол –60⁰ вокруг точки А (рис.6), то С есть точка пересечения прямой с и прямой b ¢ , получающейся из прямой b поворотом вокруг точки А на угол –60⁰.

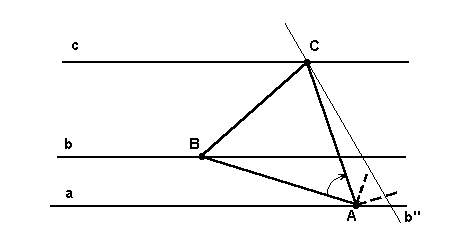
Рис. 6

Построение.

1) Выберем точку А на прямой а произвольно.

2) Построим прямую b ¢ , получающуюся из прямой b поворотом вокруг точки А на угол +60⁰ (Рис. 5).

3) В пересечении прямых b ¢ и с получаем точку С.

4) Третья вершина искомого треугольника АВС получается из точки С поворотом вокруг точки А на угол –60⁰.

Другое построение мы получим, заменяя поворот вокруг точки А на угол +60⁰ поворотом вокруг той же точки на угол –60⁰ (Рис. 6).

    Доказательство. При повороте вокруг точки А на угол –60⁰ прямая b ¢ переходит в прямую b (Рис. 5). Следовательно, точка С прямой b ¢ переходит при этом же повороте в точку, лежащую на прямой b. Иначе говоря, точка В лежит на прямой b. Далее по определению поворота, мы имеем: Ð ВАС=60⁰, АС=АВ. Поэтому D АВС – равнобедренный с углом 60⁰ при вершине; следовательно, он – равносторонний. Точно так же доказывается, что равносторонним является и изображенный на Рис. 6 треугольник.

    Исследование.  Прямая b ¢ (Рис. 5) не параллельна прямой b , т.к. угол между прямыми b и b ¢ равен 60⁰ по свойству поворота. Поэтому прямая b ¢ пересечет прямую с, параллельную прямой b, в некоторой точке С. Следовательно, D АВС всегда существует. Также всегда существует и изображенный на рисунке 132 треугольник. Поэтому при выбранной точке А задача всегда имеет два решения. (Точка А может быть выбрана на прямой а произвольно).

Метод подобия

Главная концепция метода подобия складывается в последующем: сначала строят фигуру, похожую искомой таким образом, чтобы она удовлетворяла абсолютно всем условиям задачи, помимо одного. Далее строят ранее разыскиваемую фигуру, которая похожа на искомую и удовлетворяющую опущенному требованию.

Метод подобия обретает применение, как правило, в случаях, когда из числа сведений только один считается отрезком, а все другие сведения - или углы, или взаимоотношения отрезков.

Обычно уместно дополнительную фигуру создавать таким образом, чтобы она была подобна не только лишь искомой фигуре, но и подобно расположена с ней. Результат решения находится в зависимости от выбора центра подобия. [10, с. 70]

При выполнении заданий на построение методом подобия можно воспользоваться следующим замечанием. Если две фигуры подобны, то коэффициент подобия равен отношению любых двух соответствующих отрезков. Если отрезкам a , b, c… фигуры А соответствуют отрезки a ₁ , b ₁ , c ₁ ,… подобной фигуры 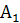, то коэффициент подобия равен также отношениям:

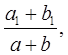
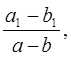
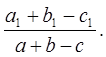
Пример 8:

Построить треугольник АВС, если известно отношение АВ: ВС, Ð АВС и радиус вписанной окружности.[20, с. 43]

Анализ. Так как в искомом треугольнике известен угол и отношение сторон этого угла, то, оставив остальные условия, построим треугольник, подобный искомому. Для этого на сторонах данного угла отложим BD, равную m каких-нибудь равных частей, и ВЕ, равную n таких же частей, и соединим точки D и E. Тогда искомый треугольник и треугольник DBE подобны, так как они имеют по равному углу, заключённому между пропорциональными сторонами. Проводя в угле АВС отрезки, параллельные DE, будем получать треугольники, подобные искомому, но с различными радиусами вписанных окружностей. Из всех этих треугольников надо выбрать один такой, чтобы радиус вписанной окружности равен r. Определив центр О, легко построить сам треугольник.

Построение:

 1. OF ^ DE;

 2. OG = r;

 3. Через G проводим AC ║ DE;

 4. ∆АВС – искомый.

Доказательство. Следует из построения.

Исследование. Возможное решение всегда одно.

Алгебраический метод

Суть метода состоит в последующем. Разрешение задач на построение объединяется к концепции определенного отрезка (либо нескольких отрезков). Значение искомого отрезка выражают посредством величины известных отрезков с поддержкой формулы. Далее создают требуемый отрезок согласно приобретенной формуле.

Пример 9:

 Провести окружность через две точки А и В так, чтобы длина касательной к ней, проведённой из точки С равнялась а. [12, с. 201]

Анализ. Пусть через точки А и В проведена окружность так, что касательная к ней из точки С равняется а. Так как через три точки можно провести окружность, то проведём СВ и определим положение точки К. Полагаем СК = х и СВ = с; тогда по свойству касательной сх = а².

Построение.

1) для построения х чертим полуокружность на ВС и дугу (С, а);

опустим LK ^ BC ;

2) с × КС = а²; поэтому х = КС, и точка К будет искомая;

3) восстановив перпендикуляры из середин АВ и КВ до их пересечения найдём искомый центр О;

4) чертим окружность (О, ОА);

МС – искомая касательная.

Доказательство. МС² = СВ × КС = 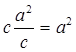 и МС = а, как и требовалось.

Исследование. Выражение a £ с – условие существования решения нашей задачи, так как только при этом условии дуга (С, а) пересечёт окружность С LB .