Метод геометрических мест

Геометрическим местом точек называется совокупность точек, обладающих свойствами, исключительно им принадлежащими. В случае если задача доводится к определению точки, то возможно оставить одно из условий, которому данная точка обязана удовлетворять; в таком случае выискиваемая точка сможет принять колоссальное число поочередных положений, и все данные утверждения составят геометрическое место точек, владеющих абсолютно всеми требуемыми свойствами, помимо откинутого. Фигура данного геометрического места чаще бывает нам заранее известна; в противоположном случае ее нужно установить добавочными построениями. Далее, приняв откинутое требование и забросив то или иное требование задания, снова узнаем, что искомая точка может осуществить колоссальное число новейших положений, производящих новейшее геометрическое место. Найдем фигуру данного новейшего геометрического места, в случае если она нам неведома. В таком случае, выискиваемая точка обязана находиться и на первом и на втором геометрическом месте, а вследствие того обусловливается их пересечением.

Порой с целью установления точки довольно создать одно геометрическое место, вследствие того то что иное предоставлено в условии задачи. В случае если же выискиваемая точка подчинена подобным условиям, которые все в совокупности характеризуют только лишь одно геометрическое место, в таком случае задача делается неопределённой. [10, с. 60]

Отсюда заметно, как немаловажно понимать разные геометрические места. Понимание геометрических мест порой дает возможность мгновенно наблюдать, в каком месте пребывает неизвестная точка.

Пример 4:

 Постройте треугольник, если задана сторона, прилежащий к ней угол и сумма двух других сторон. [19, с. 199]

Анализ. Пусть ∆АВС уже построен, тогда положение вершин В и С можно считать известным. Остаётся найти вершину А. Выясним свойства точки А. Во-первых, точка А принадлежит лучу (BA), так как дан угол АВС, во-вторых, точка А является вершиной ломанной, состоящей из двух звеньев, сумма которых равна длине данного отрезка, являющегося суммой АВ и АС сторон искомого треугольника.

На продолжении стороны ВА за точку А отложим отрезок АА₁, равный отрезку АС. Теперь можно построить треугольник А₁ВС по двум сторонам и углу между ними. В равнобедренном (по построению) треугольнике А₁АС серединный перпендикуляр к стороне А₁С пересечёт луч ВА₁ в точке А.

Построение.

1. Построить ∆ВА₁С по сторонам ВС и ВА₁ = АВ + АС и углу между ними;

2. Провести серединный перпендикуляр к стороне А₁С;

3. Найти точку пересечения луча (BA ) и построенного серединного перпендикуляра. Точка пересечения и будет искомой вершиной А.

Доказательство. В построенном ∆АВС сторона ВС, сумма сторон АВ и АС, угол В – данные.

Исследование проведём по ходу построения. Треугольник ВА₁С по двум сторонам и углу между ними можно построить единственным образом. Провести серединный перпендикуляр к отрезку А₁С – тоже единственным образом. Точка пересечения луча ( BA ) и серединного перпендикуляра существует, и она единственная.

3.2. Методы геометрических преобразований

Некоторые геометрические задачи можно решать несколькими способами. Но в разных случаях решения будут разные по понятности и сложности. Геометрические преобразования значительно упрощают целый ряд геометрических задач на доказательство, вычисление и построение.

В работе приведены решения задач на построение с использованием метода симметрии, метода параллельного переноса, метода поворота и метода подобия.

Метод симметрии

Может случиться, что фигура, которую требуется построить, имеет точки, симметричные относительно некоторой прямой или точки. В таком случае целесообразно выполнить преобразование симметрии относительно этой прямой или точки.

Проиллюстрируем метод симметрии на следующих примерах.

Пример 5:

Дан угол АВС и точка О внутри него. Провести через точку О прямую, отрезок которой заключенный между сторонами угла, делился в точке О пополам.

Решение.

Анализ. Предположим, что задача решена и MN – искомая прямая (рис. 3).

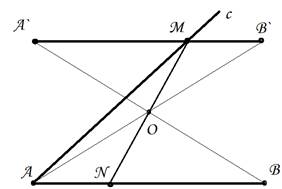
Рис. 3

Примем точку О за центр симметрии. Тогда точки М и N симметричны относительно точки О. Пусть прямая А ¢ В ¢ симметрична АВ относительно точки О. Так как точка М симметрична точке N, лежащей на прямой АВ, то прямая А ¢ В ¢ должна пройти через точку М.

Таким образом, точка М должна быть точкой пересечения прямых ВС и А ¢ В ¢ .

Построение.

1. Строим прямую А ¢ В ¢ , симметричную прямой АВ относительно центра О (для этого находим точку А ¢ , симметричную точке А, и В ¢ , симметричную В относительно точки О).

2. Находим точку пересечения М прямых ВС и А ¢ В ¢ и соединяем её с точкой О. Получим искомую прямую MN.

Доказательство вытекает из анализа и построения, поэтому его опустим.

Исследование.

Из анализа и построения можно сделать вывод о том, что задача всегда имеет только одно решение.