КУРСОВАЯ РАБОТА
Выполнила:
студентка 4 курса очной формы обучения
Цунаева Виктория Сергеевна
Руководитель:
кпн, доцент кафедры математики и МПМД
Ветошкина Е.С.
Итоговая оценка - ______________
Подпись______________________
Коломна – 2019 г.
Содержание
Введение. 4
§ 1. Методические аспекты обучения решению задач и анализ учебной литературы по геометрии. 6
1.1 Значение задач на построение в школьном курсе геометрии. 6
1.2 Сравнительный анализ школьных учебников геометрии. 10
§ 2. Методика решения задач на построение. 19
2.1. Анализ. 19
2.2. Построение. 19
2.3. Доказательство. 20
2.4. Исследование. 21
§ 3. Методы решения задач на построение. 22
3.1. Метод геометрических мест. 22
3.2. Методы геометрических преобразований. 23
3.2.1. Метод симметрии. 24
3.2.2. Метод параллельного переноса. 25
3.2.3. Метод поворота. 26
3.2.4. Метод подобия. 28
3.3. Алгебраический метод. 29
§ 4. Компьютерная поддержка в обучении задач на построение. 31
4.1. Роль компьютерных программ при решении задач на построение. 31
4.2. Динамическая геометрическая среда GeoGebra. 34
Заключение. 45
Список литературы.. 47
Введение
Изменения в науке, технике и производстве предъявляют новые требования к математической подготовке современного ученика ХХI века. Проблема формирования конструктивно – геометрических умений и навыков учащихся является важным фактором, способствующим общекультурному развитию человека, его готовности к непрерывному образованию и профессиональной деятельности как в технической, так и любой другой сфере.
Актуальность выбранной курсовой работы объясняется тем, что как только ученики начинают выполнять геометрические построения, у них улучшается математическое развитие. Задачи на построение вырабатывают и помогают лучше представить конкретную геометрическую фигуру и дополнительные элементы. Все это помогает развивать пространственное мышление школьников. Также геометрические задачи на построение способны повысить уровень логического мышления, интуиции, внимания, целеустремленности, изобретательности, дисциплинированности и трудолюбия.
Исходя из вышесказанного, проблема исследования состоит в следующем: рассмотрение различных методов решения геометрических задач на построение.
Объект исследования – процесс обучения геометрии учащихся 7 – 9 классов.
Предмет исследования – процесс обучения решению задач на построение.
Цель исследования – изучить методику решения задач на построение в школьном курсе геометрии.
В соответствии с проблемой, объектом, целью были намечены следующие задачи исследования:
1. Провести анализ школьных учебников разных авторов;
2. Рассмотреть главные этапы решения задач на построение;
3. Рассмотреть методы решения задач на построение;
4. Осуществить ознакомление с компьютерной программой GeoGebra.
Структура работы: работа состоит из введения, четырех параграфов, заключения, списка использованных источников.
Методические аспекты обучения решению задач и анализ учебной литературы по геометрии
Методика решения задач на построение
Одной из основных проблем методики обучения решению задач на построение является методика введения и изучения этапов решения конструктивных задач. Еще в IV в. до н. э. древнегреческие геометры разработали общую схему решения задач на построение, которой мы пользуемся и теперь. Процесс решения задачи разбивают на 4 этапа: анализ, построение, доказательство и исследование. Рассмотрим каждый этап более подробно.
Анализ
Анализ — это важный этап решения задачи, который мы понимаем, как поиск способа решения задачи на построение. На этом этапе должны быть подмечены такие зависимости между данными фигурами и искомой фигурой, которые позволили бы в дальнейшем построить эту искомую фигуру (если мы знаем, как строить искомую фигуру, то никакой анализ уже не нужен).
Анализ – подготовительный, предварительный этап решения задачи на построение.
Пример 3:
Постройте остроугольный треугольник АВС по сумме углов В и А, высоте В D и стороне АС.
Анализ: дан угол, представляющий сумму углов А и В, отрезок АС и отрезок В D. Требуется построить такой треугольник АВС, в котором угол С1= 1800 – (угол А1+ угол В1), высота B 1 D 1 равна отрезку В D, сторона А1С1 равна отрезку АС. Допустим, что такой треугольник построен. Нам известна сумма углов А и В, следовательно, мы можем найти угол С1. Затем построим ∆СВ D по катету и противолежащему углу. А потом достроим ∆АВС.
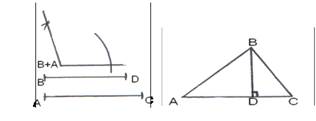
Построение
Второй этап решения задач на построение состоит из двух частей:
· перечисление в определенном порядке всех элементарных построений, которые нужно выполнить, согласно анализу, для решения задачи;
· непосредственное выполнение этих построений на чертеже при помощи чертежных инструментов. Действительно, решить задачу с помощью тех или иных инструментов — значит указать конечную совокупность элементарных, допустимых для данных инструментов, построений, выполнение которых в определенной последовательности позволяет дать ответ на вопрос задачи.
Построение:
1. Построить прямую а.
2. Построить перпендикуляр (прямая b) к прямой а.
3. Отложить отрезок В1 D 1, равный В D.
4. Построить отдельно угол С1= 1800 – (угол А1+ угол В1).
5. Построить угол В1=900 – угол С1.
6. С1 – точка пересечения.
7. На прямой b провести окружность R =АС и с центром С1.
8. А1 - точка пересечения.
9. А1 и В1 соединить.
10. ∆А1В1С1 – искомый.
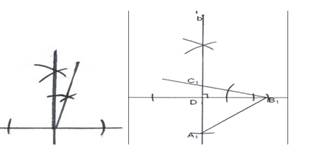
Доказательство
После того как фигура построена, необходимо установить, удовлетворяет ли она условиям задачи, то есть показать, что фигура, полученная из данных элементов определенным построением, удовлетворяет всем условиям задачи. Значит, доказательство существенно зависит от способа построения. Одну и ту же задачу можно решать различными способами, в зависимости от намеченного при анализе плана построения, а поэтому, и доказательство в каждом случае будет свое.
Доказательство:
1. В D = B 1 D 1(по построению).
2. угол С1= 1800 – (угол А1+ угол В1) (по построению).
3. А1С1 = АС (по построению).
4. ∆А1В1С1 – искомый.
Исследование
При построении обычно ограничиваются отысканием одного какого-либо решения, причем предполагается, что все шаги построения действительно выполнимы. Для полного решения задачи нужно еще выяснить следующие вопросы: 1) всегда ли (то есть при любом ли выборе данных) можно выполнить построение избранным способом; 2) можно ли и как построить искомую фигуру, если избранный способ нельзя применить; 3) сколько решений имеет задача при каждом возможном выборе данных? Рассмотрение всех этих вопросов и составляет содержание исследования.
Таким образом, исследование имеет целью установить условия разрешимости и определить число решений.
Исследование: Данная задача всегда имеет решение.
Метод геометрических мест
Геометрическим местом точек называется совокупность точек, обладающих свойствами, исключительно им принадлежащими. В случае если задача доводится к определению точки, то возможно оставить одно из условий, которому данная точка обязана удовлетворять; в таком случае выискиваемая точка сможет принять колоссальное число поочередных положений, и все данные утверждения составят геометрическое место точек, владеющих абсолютно всеми требуемыми свойствами, помимо откинутого. Фигура данного геометрического места чаще бывает нам заранее известна; в противоположном случае ее нужно установить добавочными построениями. Далее, приняв откинутое требование и забросив то или иное требование задания, снова узнаем, что искомая точка может осуществить колоссальное число новейших положений, производящих новейшее геометрическое место. Найдем фигуру данного новейшего геометрического места, в случае если она нам неведома. В таком случае, выискиваемая точка обязана находиться и на первом и на втором геометрическом месте, а вследствие того обусловливается их пересечением.
Порой с целью установления точки довольно создать одно геометрическое место, вследствие того то что иное предоставлено в условии задачи. В случае если же выискиваемая точка подчинена подобным условиям, которые все в совокупности характеризуют только лишь одно геометрическое место, в таком случае задача делается неопределённой. [10, с. 60]
Отсюда заметно, как немаловажно понимать разные геометрические места. Понимание геометрических мест порой дает возможность мгновенно наблюдать, в каком месте пребывает неизвестная точка.
Пример 4:
Постройте треугольник, если задана сторона, прилежащий к ней угол и сумма двух других сторон. [19, с. 199]
Анализ. Пусть ∆АВС уже построен, тогда положение вершин В и С можно считать известным. Остаётся найти вершину А. Выясним свойства точки А. Во-первых, точка А принадлежит лучу (BA), так как дан угол АВС, во-вторых, точка А является вершиной ломанной, состоящей из двух звеньев, сумма которых равна длине данного отрезка, являющегося суммой АВ и АС сторон искомого треугольника.
На продолжении стороны ВА за точку А отложим отрезок АА1, равный отрезку АС. Теперь можно построить треугольник А1ВС по двум сторонам и углу между ними. В равнобедренном (по построению) треугольнике А1АС серединный перпендикуляр к стороне А1С пересечёт луч ВА1 в точке А.
Построение.
1. Построить ∆ВА1С по сторонам ВС и ВА1 = АВ + АС и углу между ними;
2. Провести серединный перпендикуляр к стороне А1С;
3. Найти точку пересечения луча (BA ) и построенного серединного перпендикуляра. Точка пересечения и будет искомой вершиной А.
Доказательство. В построенном ∆АВС сторона ВС, сумма сторон АВ и АС, угол В – данные.
Исследование проведём по ходу построения. Треугольник ВА1С по двум сторонам и углу между ними можно построить единственным образом. Провести серединный перпендикуляр к отрезку А1С – тоже единственным образом. Точка пересечения луча ( BA ) и серединного перпендикуляра существует, и она единственная.
3.2. Методы геометрических преобразований
Некоторые геометрические задачи можно решать несколькими способами. Но в разных случаях решения будут разные по понятности и сложности. Геометрические преобразования значительно упрощают целый ряд геометрических задач на доказательство, вычисление и построение.
В работе приведены решения задач на построение с использованием метода симметрии, метода параллельного переноса, метода поворота и метода подобия.
Метод симметрии
Может случиться, что фигура, которую требуется построить, имеет точки, симметричные относительно некоторой прямой или точки. В таком случае целесообразно выполнить преобразование симметрии относительно этой прямой или точки.
Проиллюстрируем метод симметрии на следующих примерах.
Пример 5:
Дан угол АВС и точка О внутри него. Провести через точку О прямую, отрезок которой заключенный между сторонами угла, делился в точке О пополам.
Решение.
Анализ. Предположим, что задача решена и MN – искомая прямая (рис. 3).
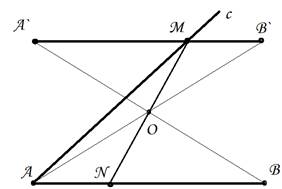
Рис. 3
Примем точку О за центр симметрии. Тогда точки М и N симметричны относительно точки О. Пусть прямая А ¢ В ¢ симметрична АВ относительно точки О. Так как точка М симметрична точке N, лежащей на прямой АВ, то прямая А ¢ В ¢ должна пройти через точку М.
Таким образом, точка М должна быть точкой пересечения прямых ВС и А ¢ В ¢ .
Построение.
1. Строим прямую А ¢ В ¢ , симметричную прямой АВ относительно центра О (для этого находим точку А ¢ , симметричную точке А, и В ¢ , симметричную В относительно точки О).
2. Находим точку пересечения М прямых ВС и А ¢ В ¢ и соединяем её с точкой О. Получим искомую прямую MN.
Доказательство вытекает из анализа и построения, поэтому его опустим.
Исследование.
Из анализа и построения можно сделать вывод о том, что задача всегда имеет только одно решение.
Метод поворота
Метод поворота при в решении задач на построения состоит в том, что отдельные элементы фигуры поворачиваются с целью получения новой фигуры, построение которой известно. Приведем пример, иллюстрирующий применение этого метода.
Пример 7:
Даны три параллельные прямые a, b и с. Построить равносторонний треугольник АВС, вершины А, В, С которого лежат на данных прямых.
Решение.
Анализ. Предположим, что задача решена и D АВС – искомый (рис.5).
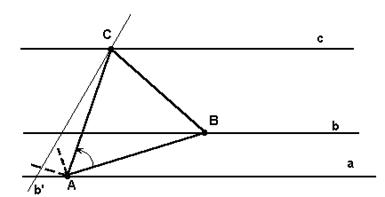
Рис. 5
Так как АВ=АС и Ð ВАС=600, то точка В переходит в точку С при повороте вокруг точки А на угол 600 или на угол –600 (ибо Ð ВАС=+600 или –600). Пусть, например, точка В переходит в точку С при повороте вокруг точки А на угол +600. Точка В лежит на прямой b. Поэтому точка С, получающаяся из нее поворотом вокруг точки А на угол +600 должна лежать на прямой b ¢ , получающейся из прямой b поворотом вокруг точки А на угол +600. Кроме того, точка С лежит, по условию, на прямой с. Поэтому точка С есть точка пересечения прямых b ¢ и с.
Аналогично, если точка В переходит в точку С при повороте на угол –600 вокруг точки А (рис.6), то С есть точка пересечения прямой с и прямой b ¢ , получающейся из прямой b поворотом вокруг точки А на угол –600.
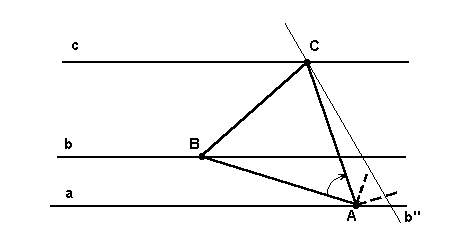
Рис. 6
Построение.
1) Выберем точку А на прямой а произвольно.
2) Построим прямую b ¢ , получающуюся из прямой b поворотом вокруг точки А на угол +600 (Рис. 5).
3) В пересечении прямых b ¢ и с получаем точку С.
4) Третья вершина искомого треугольника АВС получается из точки С поворотом вокруг точки А на угол –600.
Другое построение мы получим, заменяя поворот вокруг точки А на угол +600 поворотом вокруг той же точки на угол –600 (Рис. 6).
Доказательство. При повороте вокруг точки А на угол –600 прямая b ¢ переходит в прямую b (Рис. 5). Следовательно, точка С прямой b ¢ переходит при этом же повороте в точку, лежащую на прямой b. Иначе говоря, точка В лежит на прямой b. Далее по определению поворота, мы имеем: Ð ВАС=600, АС=АВ. Поэтому D АВС – равнобедренный с углом 600 при вершине; следовательно, он – равносторонний. Точно так же доказывается, что равносторонним является и изображенный на Рис. 6 треугольник.
Исследование. Прямая b ¢ (Рис. 5) не параллельна прямой b , т.к. угол между прямыми b и b ¢ равен 600 по свойству поворота. Поэтому прямая b ¢ пересечет прямую с, параллельную прямой b, в некоторой точке С. Следовательно, D АВС всегда существует. Также всегда существует и изображенный на рисунке 132 треугольник. Поэтому при выбранной точке А задача всегда имеет два решения. (Точка А может быть выбрана на прямой а произвольно).
Метод подобия
Главная концепция метода подобия складывается в последующем: сначала строят фигуру, похожую искомой таким образом, чтобы она удовлетворяла абсолютно всем условиям задачи, помимо одного. Далее строят ранее разыскиваемую фигуру, которая похожа на искомую и удовлетворяющую опущенному требованию.
Метод подобия обретает применение, как правило, в случаях, когда из числа сведений только один считается отрезком, а все другие сведения - или углы, или взаимоотношения отрезков.
Обычно уместно дополнительную фигуру создавать таким образом, чтобы она была подобна не только лишь искомой фигуре, но и подобно расположена с ней. Результат решения находится в зависимости от выбора центра подобия. [10, с. 70]
При выполнении заданий на построение методом подобия можно воспользоваться следующим замечанием. Если две фигуры подобны, то коэффициент подобия равен отношению любых двух соответствующих отрезков. Если отрезкам a , b, c… фигуры А соответствуют отрезки a 1 , b 1 , c 1 ,… подобной фигуры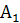 
, то коэффициент подобия равен также отношениям:
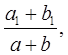
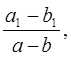
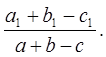
Пример 8:
Построить треугольник АВС, если известно отношение АВ: ВС, Ð АВС и радиус вписанной окружности.[20, с. 43]
Анализ. Так как в искомом треугольнике известен угол и отношение сторон этого угла, то, оставив остальные условия, построим треугольник, подобный искомому. Для этого на сторонах данного угла отложим BD, равную m каких-нибудь равных частей, и ВЕ, равную n таких же частей, и соединим точки D и E. Тогда искомый треугольник и треугольник DBE подобны, так как они имеют по равному углу, заключённому между пропорциональными сторонами. Проводя в угле АВС отрезки, параллельные DE, будем получать треугольники, подобные искомому, но с различными радиусами вписанных окружностей. Из всех этих треугольников надо выбрать один такой, чтобы радиус вписанной окружности равен r. Определив центр О, легко построить сам треугольник.
Построение:
1. OF ^ DE;
2. OG = r;
3. Через G проводим AC ║ DE;
4. ∆АВС – искомый.
Доказательство. Следует из построения.
Исследование. Возможное решение всегда одно.
Алгебраический метод
Суть метода состоит в последующем. Разрешение задач на построение объединяется к концепции определенного отрезка (либо нескольких отрезков). Значение искомого отрезка выражают посредством величины известных отрезков с поддержкой формулы. Далее создают требуемый отрезок согласно приобретенной формуле.
Пример 9:
Провести окружность через две точки А и В так, чтобы длина касательной к ней, проведённой из точки С равнялась а. [12, с. 201]
Анализ. Пусть через точки А и В проведена окружность так, что касательная к ней из точки С равняется а. Так как через три точки можно провести окружность, то проведём СВ и определим положение точки К. Полагаем СК = х и СВ = с; тогда по свойству касательной сх = а2.
Построение.
1) для построения х чертим полуокружность на ВС и дугу (С, а);
опустим LK ^ BC ;
2) с × КС = а2; поэтому х = КС, и точка К будет искомая;
3) восстановив перпендикуляры из середин АВ и КВ до их пересечения найдём искомый центр О;
4) чертим окружность (О, ОА);
МС – искомая касательная.
Доказательство. МС2 = СВ × КС =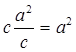 
и МС = а, как и требовалось.
Исследование. Выражение a £ с – условие существования решения нашей задачи, так как только при этом условии дуга (С, а) пересечёт окружность С LB .
Заключение
Систематическое изучение геометрических построений необходимо в школьном курсе, так как в процессе изучения задач они концентрируют в себе знания из других областей математики, развивают навыки практической графики, формируют поисковые навыки решения практических проблем, приобщают к посильным самостоятельным исследованиям, способствуют выработке конкретных геометрических представлений, а также к более тщательной обработке умений и навыков.
В работе рассмотрены:
1. Методы решения задач на построение по геометрии:
• метод геометрических мест;
• методы геометрических преобразований;
• метод симметрии;
• метод параллельного переноса;
• метод поворота;
• метод подобия;
• алгебраический метод;
2. Методика решения задач на построение по геометрии:
• анализ;
• построение;
• доказательство;
• исследование.
Цель исследования – изучить методику решения задач на построение в школьном курсе геометрии была достигнута.
В соответствии с проблемой, объектом, целью были реализованы следующие задачи исследования:
1. Проведен анализ школьных учебников по геометрии разных авторов;
2. Рассмотрены главные этапы решения задач на построение;
3. Рассмотрены методы решения задач на построение;
4. Осуществлено ознакомление с компьютерной программой GeoGebra.
При написании курсовой работы по теме исследования была изучена литература, включающая научные статьи, учебники по математике, рассмотрено практическое применение задач на построение в школьном курсе по геометрии.
Таким образом, необходимо уделять больше внимания изучению задач на построение, так как при грамотном использовании они являются мощным средством развития логического мышления учащихся; геометрические задачи на построение не нужно рассматривать как что – то отдельное, независимое от остального курса геометрии. Процессы обучения решению задач и изучение геометрии неразрывно связаны. Причем связь эта должна быть двусторонней, то есть необходимо не только обучать решению задач на построение, используя ранее полученные знания, но и, наоборот, использовать конструктивные задачи при изучении геометрии.
Список литературы
1. Александров, И.И. Сборник геометрических задач на построение с решениями / И.И.Александров. – М.: Учпедгиз,1994.
2. Аргунов, Б.И. Элементарная геометрия: учеб. пособие для пед. ин-тов / Б.И. Аргунов, М.Б. Балк. – М.: Просвещение, 2008.
3. Белошистая, А.В. Задачи на построение в школьном курсе геометрии / А. В. Белошистая // Математика в школе. – 2011. – №9. – С. 47-50.
4. Геометрия: учеб. для 7-9 кл. общеобразовательных учреждений / А. В. Погорелов. – М.: Просвещение, 2012.
5. Геометрия: учеб. для 7-9 кл. сред. шк. / А. Д. Александров, А. Л. Вернер, В.И. Рыжик. – М.: Просвещение, 2012.
6. Геометрия: учеб. для 7-9 кл. сред. шк / Л. С. Атанасян. – М.: Просвещение, 2012.
7. Геометрия: Планиметрия: 7-9 кл.: учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 2005.
8. Иванчук Н.В., Эйкен О.В., Мартынова Е.В. Использование программы GeoGebra на уроках математики в 7-11 классах: Методическое пособие. – Мурманск: МГПУ, 2008.– 36 с.
9. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ВятГГУ, 2008. – С. 59-69.
10.Мисюркеев, И.В. Геометрические построения. Пособие для учителей / И.В.Мисюркеев. – М: Учпедгиз, 1950.
11.Общая психология: учеб. для студентов пед. ин-тов / под ред. А. В. Петровского. – М.: Просвещение, 1986.
12.Прасолов, В.В. Задачи по планиметрии. Ч.1 / В.В. Прасолов. – М.: Наука, 1991.
13.Прасолов, В.В. Задачи по планиметрии. Ч.2 / В.В. Прасолов. – М.: Наука, 1991.
14.Шарыгин, И.Ф. Задачи по геометрии (Планиметрия) / И.Ф. Шарыгин. – М.: Наука, 2009.
КУРСОВАЯ РАБОТА
Выполнила:
студентка 4 курса очной формы обучения
Цунаева Виктория Сергеевна
Руководитель:
кпн, доцент кафедры математики и МПМД
Ветошкина Е.С.
Итоговая оценка - ______________
Подпись______________________
Коломна – 2019 г.
Содержание
Введение. 4
§ 1. Методические аспекты обучения решению задач и анализ учебной литературы по геометрии. 6
1.1 Значение задач на построение в школьном курсе геометрии. 6
1.2 Сравнительный анализ школьных учебников геометрии. 10
§ 2. Методика решения задач на построение. 19
2.1. Анализ. 19
2.2. Построение. 19
2.3. Доказательство. 20
2.4. Исследование. 21
§ 3. Методы решения задач на построение. 22
3.1. Метод геометрических мест. 22
3.2. Методы геометрических преобразований. 23
3.2.1. Метод симметрии. 24
3.2.2. Метод параллельного переноса. 25
3.2.3. Метод поворота. 26
3.2.4. Метод подобия. 28
3.3. Алгебраический метод. 29
§ 4. Компьютерная поддержка в обучении задач на построение. 31
4.1. Роль компьютерных программ при решении задач на построение. 31
4.2. Динамическая геометрическая среда GeoGebra. 34
Заключение. 45
Список литературы.. 47
Введение
Изменения в науке, технике и производстве предъявляют новые требования к математической подготовке современного ученика ХХI века. Проблема формирования конструктивно – геометрических умений и навыков учащихся является важным фактором, способствующим общекультурному развитию человека, его готовности к непрерывному образованию и профессиональной деятельности как в технической, так и любой другой сфере.
Актуальность выбранной курсовой работы объясняется тем, что как только ученики начинают выполнять геометрические построения, у них улучшается математическое развитие. Задачи на построение вырабатывают и помогают лучше представить конкретную геометрическую фигуру и дополнительные элементы. Все это помогает развивать пространственное мышление школьников. Также геометрические задачи на построение способны повысить уровень логического мышления, интуиции, внимания, целеустремленности, изобретательности, дисциплинированности и трудолюбия.
Исходя из вышесказанного, проблема исследования состоит в следующем: рассмотрение различных методов решения геометрических задач на построение.
Объект исследования – процесс обучения геометрии учащихся 7 – 9 классов.
Предмет исследования – процесс обучения решению задач на построение.
Цель исследования – изучить методику решения задач на построение в школьном курсе геометрии.
В соответствии с проблемой, объектом, целью были намечены следующие задачи исследования:
1. Провести анализ школьных учебников разных авторов;
2. Рассмотреть главные этапы решения задач на построение;
3. Рассмотреть методы решения задач на построение;
4. Осуществить ознакомление с компьютерной программой GeoGebra.
Структура работы: работа состоит из введения, четырех параграфов, заключения, списка использованных источников.
Методические аспекты обучения решению задач и анализ учебной литературы по геометрии
Дата: 2019-11-01, просмотров: 263.
