9.1 Основные понятия и определения
В ряде областей техники приходится иметь дело с движением различных природных жидкостей в естественном грунте. Примерами этого является движение нефти в нефтеносных пластах к нефтяным скважинам, движение грунтовых вод в водоносных пластах, используемых для целей водоснабжения, движение воды под гидротехническими сооружениями (например, плотинами) и т.д. Во всех случаях жидкость просачивается через грунт, т. е. движется внутри пор грунта, перемещаясь по мельчайшим каналам, образующимся между его частицами вследствие их неполного прилегания друг к другу. Такое движение жидкости называют фильтрацией.
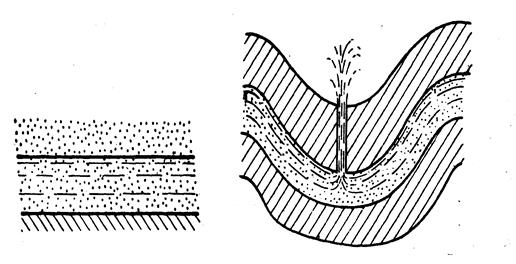
Рис.1 Рис.2
Если проницаемый пласт залегает на непроницаемом основании и не перекрывается сверху непроницаемым слоем, фильтрация происходит с образованием свободной поверхности, давление на котором равно атмосферному (рис.1). Движение в этом случае называется безнапорным. Если же фильтрация происходит в пласте, заключенном между двумя непроницаемыми пластами без образования свободной поверхности (рис.2), движение называют напорным.
Основной задачей при практических расчетах в области фильтрации является определение расхода, т.е. количества фильтрующейся жидкости и скорости фильтрации, под которой понимают расход жидкости через единицу площади поперечного сечения всего фильтрующего слоя (включая как сам грунт, так и поры между его частицами). Следует иметь в виду, что скорость фильтрации, конечно, отлична от физической скорости движения частиц жидкости по поровым каналам.
Скорость фильтрации определяется гидравлическим уклоном и физическими свойствами фильтрующейся жидкости и грунта. Физические свойства жидкости, определяются ее вязкостью и удельным весом. Фильтрационные же свойства грунта зависят от размеров и формы отдельных составляющих его частиц и характеризуются пористостью и просветом грунта.
Пористостью или иначе, коэффициентом пористости т, называется отношение объема пор, т. е. пустот между отдельными частицами грунта ко всему объему грунта:
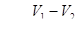 , (9.1)
, (9.1)
где 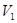 –полный объем грунта;
–полный объем грунта; 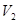 –суммарный объем твердых частиц.
–суммарный объем твердых частиц.
Под просветом, или коэффициентом просветности, понимают отношение площади сечения пор к площади всего сечения грунта. Физически просвет характеризует собой живое сечение потока фильтрующейся жидкости и определяется выражением
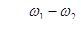 ,
, 
 (9.2)
(9.2)
где 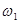 –общая площадь сечения грунта;
–общая площадь сечения грунта; 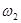 –часть этой площади, приходящаяся на долю частиц грунта.
–часть этой площади, приходящаяся на долю частиц грунта.
Пористость природных естественных грунтов изменяется в весьма широких пределах. Так, нефтеносные рыхлые (несцементированные) пески имеют пористость 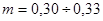 ; для песков же с глинистыми частицами и отложениями солей
; для песков же с глинистыми частицами и отложениями солей 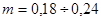 ; для известняков
; для известняков 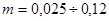 . Величина пористости естественного грунта в каждом отдельном случае может быть установлена опытным путем.
. Величина пористости естественного грунта в каждом отдельном случае может быть установлена опытным путем.
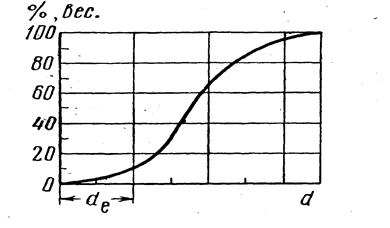
Рис.3
Естественные грунты состоят из частиц неправильной формы различных размеров; это делает теоретическое исследование фильтрации чрезвычайно сложным, и для упрощения обычно исходят из условной модели так называемого фиктивного грунта, состоящего из частиц правильной шарообразной формы одинакового диаметра, гидравлически эквивалентного естественному грунту. Значения пористости и просвета для фиктивного грунта могут быть подсчитаны теоретически. Для перехода от естественного грунта к фиктивному вводится понятие о так называемом эффективном или действующем диаметре, определяемом на основе механического анализа грунта, заключающегося в просеивании грунта через калиброванные сита отверстиями различной величины. По данным анализа строится гранулометрическая (весовая) кривая (рис.3), для чего по оси абсцисс откладывают диаметры d зерен грунта (в мм), а по оси ординат– суммарный вес всех фракций, начиная от нуля до данного диаметра в процентах от общего веса всей пробы. За эффективный диаметр принимается, например, такой диаметр зерен, при котором суммарное процентное содержание фракций более мелкого размера составляет 10% от общего веса.
9.2. Основные законы фильтрации
Первые исследования движения жидкости в пористых телах были проведены в середине ХIХ в. французским гидравликом Дарси. В своих опытах Дарси применял прибор (рис.4), состоящий из вертикального цилиндрического сосуда, заполненного слоем песка, через который при постоянной разности напора пропускалась вода.
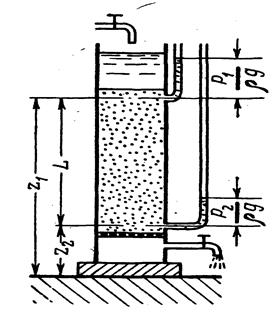
Рис.4
Определяя при помощи пьезометров давления в различных по высоте сечениях фильтрующего слоя, изменяя толщину этого слоя и состав песка и измеряя расход фильтруемом воды, Дарси установил основной закон фильтрации, которому подчиняются различные несжимаемые жидкости (вода, нефть) при своем движении через грунт. Этот закон носит название закона Дарси и имеет следующее математическое выражение:
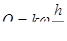 , (9.3)
, (9.3)
где Q –расход жидкости при фильтрации, 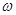 –площадь фильтрации, под которой понимают полное сечение всего фильтрующего слоя, включая как сам грунт, так и поры между отдельными его частицами (для рассматриваемого случая
–площадь фильтрации, под которой понимают полное сечение всего фильтрующего слоя, включая как сам грунт, так и поры между отдельными его частицами (для рассматриваемого случая  есть площадь поперечного сечения сосуда); h –потеря напора, равная
есть площадь поперечного сечения сосуда); h –потеря напора, равная
и определяемая по разности показаний пьезометров (здесь 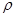 –плотность жидкости); L –толщина слоя грунта в направлении фильтрации;
–плотность жидкости); L –толщина слоя грунта в направлении фильтрации; 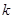 –коэффициент фильтрации, характеризующий одновременно как фильтрационные свойства пористой среды –грунта, так и физические свойства фильтрующейся жидкости.
–коэффициент фильтрации, характеризующий одновременно как фильтрационные свойства пористой среды –грунта, так и физические свойства фильтрующейся жидкости.
Уравнение (9.3) можно представить также в более простой форме
 , (9.4)
, (9.4)
где
есть средняя в сечении фильтрующего слоя скорость фильтрации, а
 ,
,
i –гидравлический уклон, представляющий собой падение напора на единицу длины.Из этой формулы следует, что коэффициент фильтрации имеет размерность
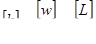 ,
,
т. е. размерность скорости (так как гидравлический уклон i есть величина безразмерная). Обычно он измеряется в см/с. Отсюда видно также, что при 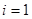
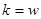 , т. е. физически коэффициент фильтрации представляет собой скорость фильтрации при единичном уклоне.
, т. е. физически коэффициент фильтрации представляет собой скорость фильтрации при единичном уклоне.
Дарси проводил свои опыты с водой. В дальнейшем при исследовании фильтрации других жидкостей было установлено, что скорость фильтрации обратно пропорциональна вязкости. В связи с этим вязкость жидкости была выделена в отдельный параметр.
В то же время скорость фильтрации стали определять не через перепад напора h , а исходя из разности давлений  , соответствующей этому перепаду (
, соответствующей этому перепаду ( 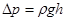 ). Таким образом,
). Таким образом,
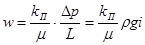 , (9.5)
, (9.5)
где 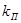 –коэффициент проницаемости, характеризующий фильтрационные свойства самого грунта;
–коэффициент проницаемости, характеризующий фильтрационные свойства самого грунта; 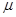 –абсолютная вязкость жидкости.
–абсолютная вязкость жидкости.
Коэффициент проницаемости связан с коэффициентом фильтрации соотношением
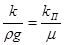 , (9.6)
, (9.6)
легко получаемым из сопоставления формул (9.4) и (9.5).
Размерность коэффициента проницаемости
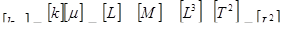 ,
,
т. е. размерность площади.
В международной системе единиц коэффициент проницаемости измеряется в м2; в физической системе единиц –в см2. За практическую же единицу коэффициента проницаемости принимают проницаемость грунта, который при площади фильтрации 
 толщине слоя фильтрации L=1см, абсолютной вязкости фильтрующейся жидкости
толщине слоя фильтрации L=1см, абсолютной вязкости фильтрующейся жидкости 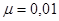 г/см·с (сП –сантипуаз) и потере давления
г/см·с (сП –сантипуаз) и потере давления  (соответствующей потере напора h ) = 1 кгс/см2 (ат) пропускает расход жидкости Q = 1 см3/с Такая единица проницаемости называется дарси (обозначается Д); единица, равная 0,001 дарси носит название миллидарси (мД):
(соответствующей потере напора h ) = 1 кгс/см2 (ат) пропускает расход жидкости Q = 1 см3/с Такая единица проницаемости называется дарси (обозначается Д); единица, равная 0,001 дарси носит название миллидарси (мД):
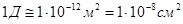 .
.
Закон Дарси часто называют законом ламинарной фильтрации, так как согласно этому закону расход и скорость фильтрации линейно зависят от потери напора, что является первым признаком ламинарного режима, что отмечалось ранее при рассмотрении движения жидкости в трубопроводах. В большинстве случаев движение жидкости в пористых телах действительно происходит с весьма малыми скоростями, и сечения отдельных пор грунта также весьма малы, что делает возможным уподобить фильтрацию ламинарному движению в тонких неправильной формы капиллярных трубках. Поэтому закон Дарси, хорошо согласующийся с действительностью, является основным законом фильтрации и обычно используется при решении различного рода практических задач в этой области.
В отдельных случаях, когда движение жидкости в грунте характеризуется значительными скоростями, что может иметь место в крупнотрещиноватых и крупнопористых породах (например, в галечниках и скальных породах), наблюдается переход к турбулентному режиму. Закон Дарси здесь нарушается, и формулы (9.3) и (9.4) неприменимы.
Закон Дарси неприменим также и при фильтрации в весьма мелких зернистых, глинистых грунтах с очень малыми скоростями, когда начинают заметно сказываться капиллярные силы поверхностного натяжения. Эти случаи не имеют, однако, особенного практического значения, так как даже при весьма малых размерах частиц грунта, диаметром всего лишь около 0,05мм, и небольших скоростях фильтрации закон Дарси все еще оказывается справедливым.
Граница перехода от ламинарного режима к турбулентному устанавливается по критическому значению числа Рейнольдса Re, для определения которого при фильтрации предложен ряд эмпирических формул. Так, по Н. Н. Павловскому.
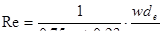 , (9.7)
, (9.7)
по В. Н. Щелкачеву
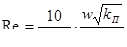 , (9.8)
, (9.8)
где 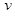 –кинематическая вязкость жидкости, а остальные обозначения те же, что и ранее.
–кинематическая вязкость жидкости, а остальные обозначения те же, что и ранее.
Критическое значение числа Рейнольдса при его определении по формуле Павловского лежит в интервале: 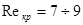 .
.
а по формуле Щелкачева 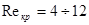 .
.
Для определения скорости фильтрации при турбулентном режиме применяются следующие формулы: формула Краснопольского (в форме, приданной ей Щелкачевым)
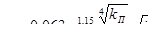 , (9.9)
, (9.9)
где 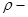 плотность жидкости, и формула Смрекера
плотность жидкости, и формула Смрекера
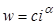 (9.10)
(9.10)
где с –коэффициент пропорциональности, определяемый опытным путем; 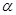 –показатель степени, изменяющийся в зависимости от вида грунта в пределах от 1/3 до 1.
–показатель степени, изменяющийся в зависимости от вида грунта в пределах от 1/3 до 1.
9.3. Определение коэффициента фильтрации
Во все формулы предыдущего параграфа, определяющие скорость фильтрации, входит коэффициент фильтрации 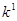 , имеющий исключительно большое значение во всех фильтрационных расчетах. Величина этого коэффициента обычно определяется опытным путем на установке, подобной изображенной на рис.4. Установку загружают опытным образцом грунта и, измеряя расход фильтрации и потерю напора, путем непосредственного вычисления по формуле (9.3) находят коэффициент фильтрации:
, имеющий исключительно большое значение во всех фильтрационных расчетах. Величина этого коэффициента обычно определяется опытным путем на установке, подобной изображенной на рис.4. Установку загружают опытным образцом грунта и, измеряя расход фильтрации и потерю напора, путем непосредственного вычисления по формуле (9.3) находят коэффициент фильтрации:
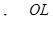 .
.
Для теоретического определения коэффициента фильтрации различными авторами предложен ряд эмпирических расчетных формул. Некоторые из них, применимые только для песчаных грунтов, приводятся ниже. В этих формулах k –коэффициент фильтрации, см/с; 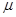 –абсолютная вязкость жидкости, П.
–абсолютная вязкость жидкости, П.
Одной из таких формул является формула Газена
 , (9.11)
, (9.11)
где de –эффективный диаметр, см, определяемый по указанному выше методу; с –некоторый коэффициент, учитывающий пористость грунта и имеющий следующие значения: для очень плотных песков с=0,8, для песков средней пористости с=1,55, для песков, составленных из округленных частиц, почти одинакового диаметра.
Для воды формула Газена может быть представлена в следующем виде:
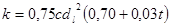 ,
,  (9.12)
(9.12)
где t –температура воды в  С.
С.
Следует иметь в виду, что формула Газена применима для грунтов с эффективным диаметром от 0,1 до 3 мм.
Приведем формулу Слихтера
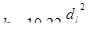 , (9.13)
, (9.13)
где 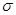 –коэффициент, зависящий от пористости т и просвета
–коэффициент, зависящий от пористости т и просвета 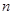 фиктивного грунта и равный
фиктивного грунта и равный  .
.
Под эффективным диаметром de в этой формуле, в отличии от формулы Газена, понимают средний весовой диаметр частиц, определенный по весовой кривой, т. е. такой диаметр, который весовые количества частиц мельче и крупнее его поровну.
Для воды при t = 10° С, когда 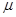 = 0,01333 П, формула Слихтера принимает вид
= 0,01333 П, формула Слихтера принимает вид
 . (9.14)
. (9.14)
При приближенных расчетах можно принимать следующие средние значения коэффициента фильтрации 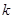 , см/с:
, см/с:
для грунтов очень большой проницаемости (средний и крупный гравий с примесью очень крупного песка) – 0,5-1;
грунтов большой проницаемости (крупный песок с мелким гравием) –0,2-0,5;
грунтов средней проницаемости (среднезернистый песок, чистый мелкий песок) – 0,1-0,2;
грунтов малой проницаемости (слабоглинистый песок, очень мелкий песок) – 0,01-0,02.
Для грунтов очень малой проницаемости Н. Н. Павловский рекомендует следующие значения 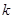 , см/с:
, см/с:
для песчаных грунтов с некоторой примесью глины – 0,006-0,007;
песчано-глинистых грунтов – 0,003-0,004;
проницаемых глин – 0,001.
9.4. Безнапорное движение грунтовых вод
В качестве примера безнапорного движения грунтовых вод paссмотрим откачку воды из колодца или скважины, заложенной в водоносном пласте с горизонтальным непроницаемым подстилающим слоем. До начала откачки грунтовые воды в пласте находятся в покое и поверхность их горизонтальна. Если откачивать воду из колодца, в водоносном слое начнется движение грунтовых вод к колодцу.
При этом уровень воды в колодце понизится. Одновременно произойдет понижение уровня грунтовых вод в пласте; это понижение будет наибольшим у стенок колодца, постепенно убывая по мере отдаления от него (рис.5). Чем интенсивнее будет производиться откачка, тем ниже будет располагаться уровень воды и колодце и тем больше будет его дебит (расход).
Уровень стояния воды в колодце до начала откачки 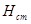 , одинаковый с уровнем во всем водоносном пласте, обычно называют статическим. Уровень
, одинаковый с уровнем во всем водоносном пласте, обычно называют статическим. Уровень 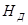 , устанавливающийся в колодце в процессе откачки, носит название динамического, а сечение открытой поверхности уровня воды в пласте вертикальной плоскостью, проходящей через ось колодца, называется кривой депрессии, или кривой падения уровня (схематически показана пунктиром на рис.6).
, устанавливающийся в колодце в процессе откачки, носит название динамического, а сечение открытой поверхности уровня воды в пласте вертикальной плоскостью, проходящей через ось колодца, называется кривой депрессии, или кривой падения уровня (схематически показана пунктиром на рис.6).

Рис.5 Рис.6
В действительности кривая дисперсии выклинивается на стенках колодца несколько выше поверхности воды в нем, образуя так называемый «промежуток высачивания» (рис.6). На этом промежутке ВС вода будет сочиться в атмосферу и стекать в колодец вдоль его стенок. Действительная кривая депрессии изображается кривой АВСС'В'A'.
При откачке из одиночного колодца (скважины) снижение уровня, вызываемое откачкой, на некотором расстоянии от оси колодца практически перестает быть заметным; это расстояние называется радиусом дренирования, или радиусом влияния колодца (скважины). При предварительных расчетах его можно принимать равным для песчаных грунтов от 350 до 500 м, для крупнозернистых грунтов –700 м.
Предполагая этот радиус R известным, зная толщину (мощность) водоносного слоя и задаваясь динамическим уровнем в колодце, можно определить расход воды в колодце и установить приближенную форму депрессионной кривой.
Для этого рассмотрим движение воды через некоторое цилиндрическое сечение водоносного слоя на расстоянии х от оси колодца. Если глубина воды в этом сечении 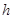 , площадь сечения будет равна
, площадь сечения будет равна
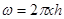 .
.
При этом расход фильтрации

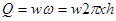 ,
,
где w –скорость фильтрации, определяемая, как обычно, по формуле Дарси (9.4),
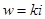 .
.
Подставляя это значение скорости в выражение для расхода, получаем
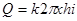 .
.
Гидравлический уклон 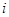 в этом выражении можно заменить через отношение бесконечно малой потери напора, т. е. падения уровня dh , бесконечно малому пути в радиальном направлении dx .
в этом выражении можно заменить через отношение бесконечно малой потери напора, т. е. падения уровня dh , бесконечно малому пути в радиальном направлении dx .

 .
.
Тогда  .
.
Разделив переменные

и проинтегрировав это уравнение в пределах для 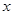 от
от 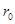 до
до 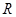 (где
(где 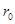 –радиус колодца) и соответственно для
–радиус колодца) и соответственно для 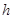 от
от 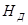 до
до 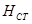 , т. е. пренебрегая участком высачивания
, т. е. пренебрегая участком высачивания
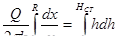 ,
,
получим следующее выражение:
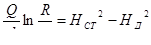 , (9.15)
, (9.15)
известное под названием формулы Дюпюи.
Расход, т.е. искомый дебит колодца, определяется выражением
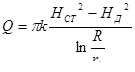 . (9.16)
. (9.16)
Для определения формы кривой депрессии необходимо, задаваясь различными значениями х (вместо R ), определить из уравнения (9.15) соответствующие им значения h ( вместо 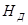 ) и по точкам построить кривую, которая представляет собой параболу в координатах
) и по точкам построить кривую, которая представляет собой параболу в координатах  ,
, 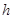 .
.
Опытными проверками установлено, что расход, определяемый по формуле Дюпюи, совпадает с действительным расходом, не смотря на неучет промежутка высачивания; положение же кривой депрессии при этом, естественно, определяется лишь приближенно.
9.5. Напорное движение грунтовых вод
Рассмотрим случай, когда водоносный пласт располагается между двумя водонепроницаемыми слоями и находится под избы точным давлением.
Если в таком пласте заложить колодец (скважину) и из него откачать воду, то толщина водоносного слоя, в отличие от случая, рассмотренного в предыдущем параграфе, не изменится, а изменится давление в пласте, убывая по направлению к колодцу. Отметим, что в тех случаях, когда глубина колодца меньше напора, соответствующего давлению в пласте до начала откачки, колодец будет фонтанировать и вода самоизливаться на поверхность земли.
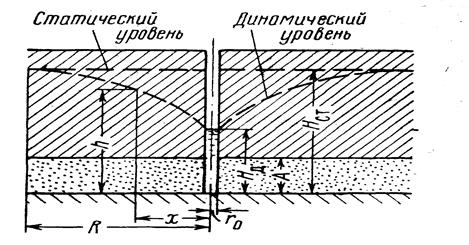
Рис.7
Подобного рода колодцы (скважины) обычно называют артезианскими. Пусть (рис.7). Толщина водоносного слоя будет А, напор в пласте на расстоянии R (радиус влияния) от оси колодца 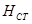 и высота уровня в колодце после откачки
и высота уровня в колодце после откачки 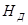 . Тогда, по аналогии с предыдущим, расход воды, проходящей через цилиндрическое сечение водоносного пласта, взятое на расстоянии х от оси колодца, будет
. Тогда, по аналогии с предыдущим, расход воды, проходящей через цилиндрическое сечение водоносного пласта, взятое на расстоянии х от оси колодца, будет
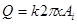 ,
,
где i –по-прежнему гидравлический уклон. Подставляя сюда вместо i его значение, равное 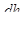 , разделяя переменные и интегрируя выражение
, разделяя переменные и интегрируя выражение
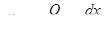
в пределах для х от 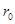 до
до 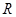 и для h от
и для h от 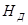 до
до 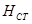 , получаем
, получаем
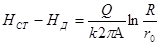 .
.
При этом дебит артезианского колодца при напорной фильтрации определяется выражением
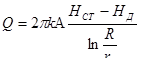 . (9.17)
. (9.17)
Так как последнее уравнение дает прямую линейную зависимость дебита от понижения уровня воды в колодце, для характеристики напорного водоносного пласта иногда вводят также понятие о так называемом удельном дебите, понимая под последним величину дебита при понижении уровня воды в колодце на 1 м.
Удельный дебит обычно определяется опытным путем на основании пробных откачек:
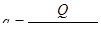 . (9.18)
. (9.18)
Дата: 2019-11-01, просмотров: 470.