В практической деятельности часто приходится сталкиваться с различными случаями истечения жидкости из отверстий и протеканием ее через патрубки, называемые насадками (в эжекторах, т.е. водоструйных насосах, в гидромониторах, гидротурбинах, карбюраторах, пожарных устройствах, при опорожнении различных емкостей и т.д.).
При истечении жидкости через отверстие, сделанное в боковой стенке или дне сосуда, вся жидкость, находящаяся в нем, приходит в движение. Однако потери напора в сосуде будут ничтожны. Поэтому скорость подхода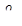 
(рис.1), т.е. средняя скорость в «подходном» плоском живом сечении 1–1 будет также незначительной. Обозначим через 
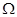площадь «подходного» живого сечения 1–1, а через 
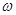–площадь отверстия. В случае, если 
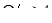, скоростью подхода можно пренебрегать, так как ошибка при этом будет менее 5%.
Тогда можно считать, что
.
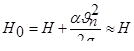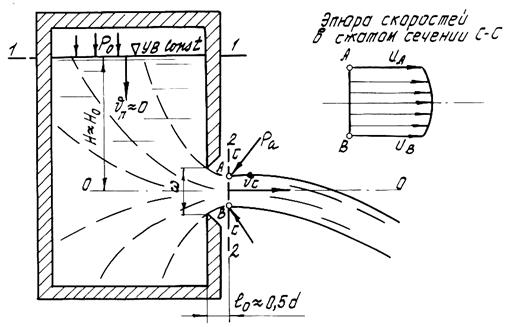
Рис.1
Основным вопросом при изучении истечения жидкости из отверстий и насадков является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.
Рассмотрим случай истечения жидкости через малое отверстие в тонкой стенке (рис.1). Малым будем называть отверстие, которое одновременно удовлетворяет двум условиям:
1) скорость подхода пренебрежимо мала, т.е. соблюдается неравенство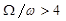 
;
2) скорости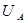 
и 
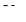(в верхней и нижней точках сжатого живого сечения) примерно равны друг другу, т.е. 
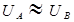(это наблюдается когда 
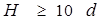, где d –высота отверстия).
Под тонкой стенкой понимается такая стенка, у которой края отверстия имеют заостренную кромку. При этом кромка заострена так, что вытекающая из отверстия струя касается стенки по одной линии. В этом случае возможны только местные сопротивления движению жидкости.
Сжатие струи от 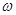до 
обусловлены инерцией частиц жидкости, движущихся при подходе к отверстию по различным криволинейным траекториям.
На пути от выхода из отверстия до сжатого сечения С–С движение резко изменяющееся, а после него – плавно изменяющееся.
Сжатое сечение С–С является первым (после выхода из отверстия) сечением, к которому можно применить уравнение Бернулли, так как линии тока в сжатом сечении близки к параллельном прямым, а скорости здесь распределяются примерно равномерно и эпюра скоростей близка к прямоугольнику.
Введем обозначение
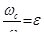, (6.1)
где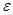 
– коэффициент сжатия струи.
Найдем среднюю скорость 
в сжатом сечении и расход Q жидкости, вытекающей из сосуда. Для решения этой задачи соединим уравнением Бернулли сечения 1–1 и 2–2, первое из которых совпадает с поверхностью жидкости в сосуде (подходное сечение), а второе проходит через сжатое сечение С–С. Плоскость сравнения 0–0 проведем через центр тяжести сечения С–С:
,
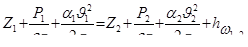где
; 
; 
; 
;
; 
; 
.
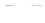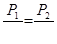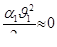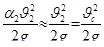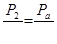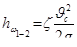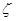–коэффициент сопротивления, учитывающий потери полного напора от сечения 1–1 до сечения 2–2.
Следует иметь в виду, что потери напора сосредотачиваются в основном в районе самого отверстия, где скорости уже достаточно велики:
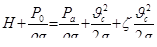. (6.2)
Обозначим
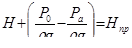, (6.3)
где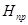 
–приведенный напор.
Тогда
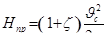, (6.4)
откуда
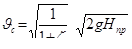, (6.5)
или
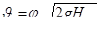, (6.6)
где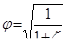 
–коэффициент, учитывающий потери напора и называемый коэффициентом скорости.
При 
, следовательно,
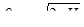. (6.7)
Для идеальной жидкости
,
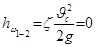т.е. в этом случае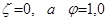 
.
Следовательно, для идеальной жидкости
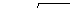. (6.8)
Эта формула называется формулой Торичелли.
Зная скорость в сжатом сечении, найдем расход Q для случая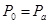 
. Очевидно, что
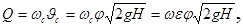
или окончательно
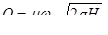(6.9)
Для круглых и квадратичных отверстий (по опытным данным) для квадратичной области сопротивления:
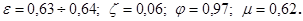
В случае истечения жидкости под уровень (случай затопленного отверстия) в формуле для расхода (6.9) вместо H подставляется Z –разность уровней жидкости в сосудах (рис.2).
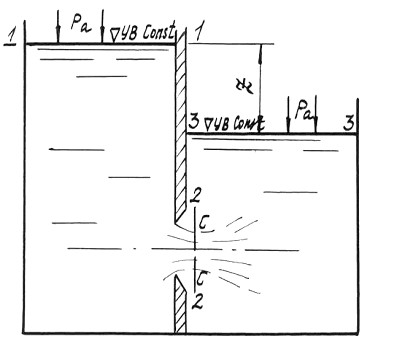
Рис.2
,
,
.
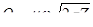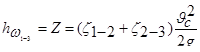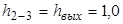6.2. Истечение жидкости из насадков при постоянном напоре
Рассмотрим истечение жидкости в атмосферу через внешний круглоцилиндрический насадок (насадок Вентури) – рис.3:
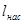–длина насадка;
–площадь поперечного сечения насадка на выходе;
–площадь отверстия, к которому присоединен насадок.
Как видим, при выходе в среду атмосферного давления сжатие струи отсутствует.
Водоворотная область так же, как и транзитная струя в пределах этой области, характеризуется наличием вакуума. Причем максимальный вакуум наблюдается в сечении С–С, где струя имеет наибольшее сжатие и где скорости в транзитной струе, а также кинетическая энергия жидкости оказываются наибольшими.
Известно, что с возрастанием кинетической энергии потока в рассматриваемом сечении потенциальная энергия должна уменьшаться.
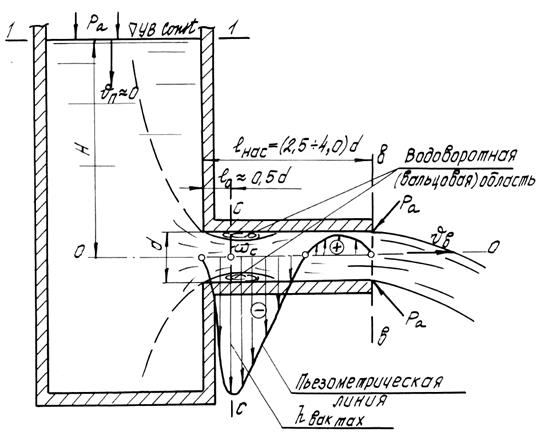
Рис.3
Если в сечении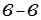 
имеем атмосферное давление, то, двигаясь от этого сечения против течения и попадая в область, где скорости благодаря сжатию струи оказываются большими, чем в сечении 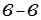, мы получим давление в этой области меньше, чем в сечении 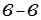, т.е. меньше атмосферного давления.
Пьезометрическая линия для насадка в соответствии со сказанным получает вид, показанный на рис.2.
Найдем расчетные зависимости для и Q. Для этой цели соединим уравнения Бернулли сечения 1–1 и 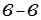(см.рис.3) и , рассуждая точно так же, как и в случае истечения жидкости через отверстия, получаем следующие расчетные формулы:
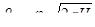, (6.10)
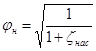. (6.11)
Расход Q при истечении из насадка
,
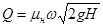где –коэффициент расхода насадка,
,
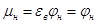так как для насадка коэффициент сжатия, отнесенный к сечению 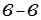, где давление атмосферное, равен единице, то есть 
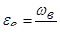=1,0.
Численные значения коэффициентов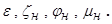 
Коэффициент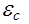 
для сечения С–С равняется коэффициенту сжатия при истечении от отверстия в тонкой стенки, т.е.
.
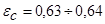Коэффициент сопротивления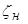 
, при истечении из насадка в атмосферу, равен коэффициенту сопротивления на вход в трубу, т.е.
.
При истечении под уровень
.
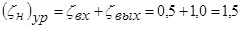Коэффициенты скорости 
и расхода 
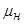насадка как в случае истечения в атмосферу, так и в случае истечения под уровень, равны, т.е.
,
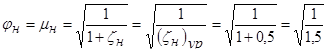или
.
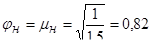Сопоставим расходы и скорости при истечении жидкости через круглое отверстие в тонкой стенке и через насадок Вентури, приставленный к этому отверстию:
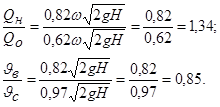
Как видно, внешний цилиндрический насадок, присоединенный к отверстию, дает следующий эффект:
а) расход жидкости, вытекающей из сосуда, увеличивается на 34%;
б) скорость истечения жидкости уменьшается на 15%.
Увеличение расхода обусловлено наличием вакуума в насадке. Благодаря вакууму напор истечения вырастает, становясь равным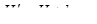 
. Уменьшение же скорости обусловлено увеличением потерь напора в связи с расширением струи в насадке (между сечениями С–С и ).
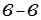Величину вакуума в сечении С–С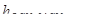 
можно найти, если соединить уравнение Бернулли сечения С–С и .
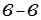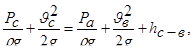(6.12)
где
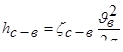; (6.13)
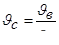. (6.14)
Подставив (6.13) и (6.14) в (6.12), получаем
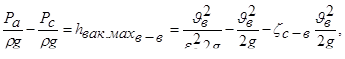(6.15)
или
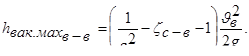(6.16)
Подставив в (16) вместо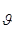 
его значение из формулы (10), будем иметь
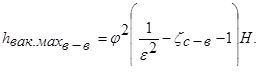(6.17)
Если в (6.17) подставить численные значения коэффициентов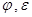 
и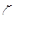 
, получим
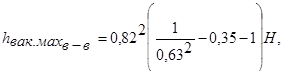
или
(6.18)
6.3. Свободные струи. Общие сведения
Струи движутся по инерции под влиянием начальной скорости, созданной давлением или силой тяжести.
Струя, не ограниченная твердыми стенками, называется свободной. Другими словами, струя жидкости – это поток, живые сечения которого не ограничены твердыми стенками.
Свободные струи бывают затопленными и незатопленными.
Струю считают затопленной, если она распространяется в пространстве, занятом такой же жидкостью. Например, струя воды, выходящая из отверстия в стенке резервуара при истечении «под уровень», или струя воздуха, выходящая из отверстия замкнутого резервуара в атмосферу в условиях одной и той же плотности воздуха. В противном случае струю считают незатопленной (например, струя воды при истечении из резервуара в атмосферу, когда эта струя находится в свободном полете).
К незатопленным свободным струям относятся пожарные и фонтанные струи, а также струи, получаемые при помощи дождевальных аппаратов и гидромониторов, и т.п.
Режим течения струй может быть ламинарным и турбулентным. Чаще всего приходится встречаться с турбулентными струями.
В настоящее время теория свободных струй и методы из практического применения составляют обширный раздел гидравлики. В СССР этот вопрос наиболее подробно исследовался в ЦАГИ (работы Г.Н. Абрамовича и др.).
6.4. Затопленная турбулентная струя
Теоретические и экспериментальные исследования показали, что струя жидкости, выходящая из насадка (при плавном очертании входа в него), постепенно расширяется в виде конуса и благодаря вязкости увлекает в движение окружающую её жидкость. Вместе с тем между струей и жидкостью внешнего пространства происходит обмен масс (вследствие наличия пульсационных скоростей, поперечных по отношению к поверхности раздела). В процессе этого обмена струя захватывает несколько большую массу, так что в направлении движения струи ее масса несколько увеличивается.
Структура струи.
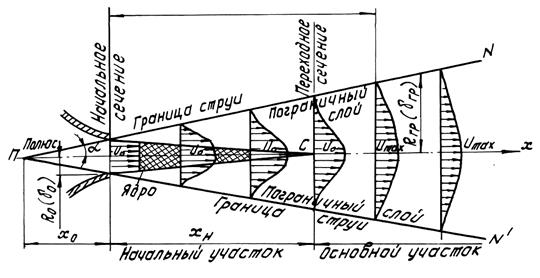Рис.4
Сечение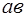 
струи, совпадающее с выходным сечением насадка или трубы, называется начальным сечением струи (рис.4). В этом сечении скорости во всех его точках равны между собой. На протяжении длины 
(на так называемом начальном участке) осевая скорость постоянная по величине и равна скорости 
в выходном сечении. Далее осевая скорость постепенно уменьшается. Участок струи, на котором осевая скорость 
, называется основным, а сечение струи, отделяющее начальный участок от основного, – переходным. В области авс во всех точках струи скорости жидкости равны между собой и равны 
. Эта область называется ядром струи.
Опытами установлено, что ядро с боков ограничено практически прямыми линиями. Эти прямые отделяют ядро от окружающего его турбулентного пограничного слоя, в пределах которого скорости изменяются. Внешние границы турбулентного пограничного слоя считают очерченными прямыми линиями. Точка О пересечения этих прямых называется полюсом струи.
Исследования показали, что при равномерном распределении скоростей в начальном сечении гидродинамическое давление в струе почти равно давлению в окружающей среде (жидкости).
Если на одном и том же чертеже в одном и том же масштабе построить эпюры скоростей для ряда поперечных сечений основного участка, то получим картину, показанную на рис.5.
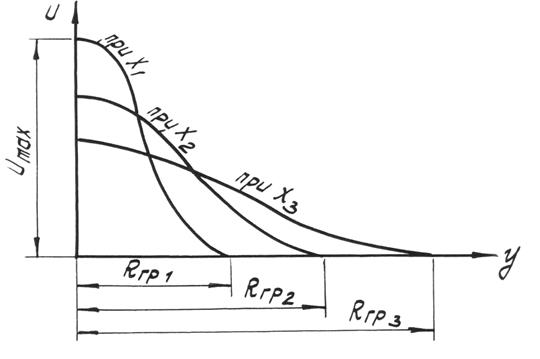
Рис.5
Для всех эпюр скоростей характерно следующее: если вместо абсолютных принять относительные скорости, например, отношение скорости в произвольной точке 1, находящейся на расстоянии от оси струи (рис.6) к скорости, равной половине осевой, т.е. к скорости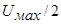 
, в точке, расположенной на расстоянии 
от оси, то эпюры скоростей во всех поперечных сечениях струи будут тождественны.
Алгебраически это будет выглядеть так: функция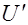 
координаты одна и та же для всех поперечных сечений струи, т.е.
,
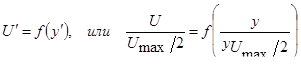что указывает на некоторое подобие между собой всех эпюр скоростей.
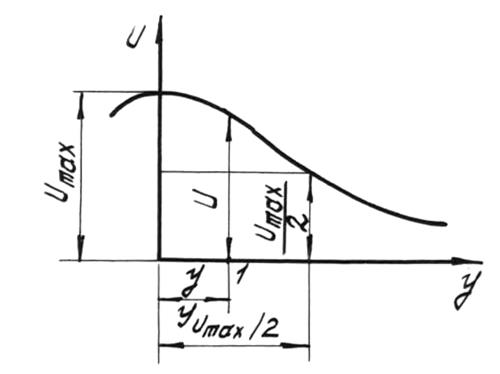
Рис.6
Последнюю зависимость можно прочитать так: для сходственных точек всех поперечных сечений отношение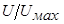 
есть величина постоянная:
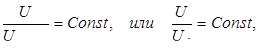
где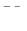 
–скорость в произвольной точке сечения струи.
Однако это подобие эпюр скоростей не следует понимать как простое геометрическое подобие между ними. Это подобие представляет собой некоторое однообразие в форме эпюры. Оно заключается, по существу, в одной и той же закономерности распределения скоростей во всех сечениях основного участка струи. В связи с этим, если известны эпюра скоростей и закономерность изменения скорости в какой-либо характерной точке сечения, например в осевой точке 
, то этим полностью определяется все поле скоростей струи.
Г.Н. Абрамович дает следующее уравнение осевой скорости для круглой струи:
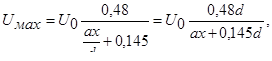(6.19)
где x –расстояние от «полюса» до рассматриваемого сечения струи; d –диаметр выходного отверстия; a –коэффициент турбулентности или коэффициент структуры, учитывающий структуру потока в выходном сечении.
Для практических расчетов можно принимать a=0,08.
Все параметры круглой струи определяются по формулам
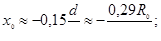(6.20)
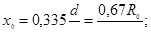(6.21)
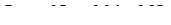; (6.22)
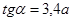. (6.23)
6.5. Незатопленная турбулентная струя
В этой струе можно выделить три характерные части: компактную, раздробленную и распыленную (рис.7).
В пределах компактной части струя сохраняет цилиндрическую форму, а сплошность потока еще не нарушается. В пределах раздробленной части сплошность струи нарушается, причем наблюдается ее постепенное расширение. Наконец, в пределах распыленной части струи происходит распад потока на отдельные капли. Разрушение струи, т.е. ее раздробление, а затем и распыление, объясняется аэрацией струи. Аэрация же, в свою очередь, обусловливается действием сил собственного веса жидкости и сил сопротивления воздуха, вызывающих турбулентный обмен частиц через границу между воздушной и водяной средами.
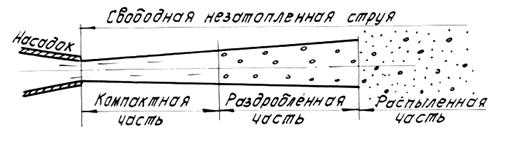
Рис.7
Уравнение теоретической траектории свободной струи выводится из предположения, что все частицы движутся совершенно одинаково, причем каждая, как свободная материальная точка в пустоте. В этом случае уравнение траектории (рис.8) в параметрической форме может быть представлено в виде:
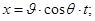(6.24)
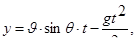(6.25)
где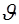 
–начальная скорость; 
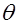–угол наклона вектора начальной скорости к горизонту; 
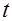–время.
Исключая время, получим
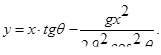(6.26)
Полагая в последней формуле y =0, определим 
–теоретическую дальность полета струи (дальность боя), откуда следует, что теоретическая максимальная дальность боя будет при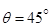 
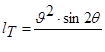, (6.27)
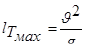. (6.28)
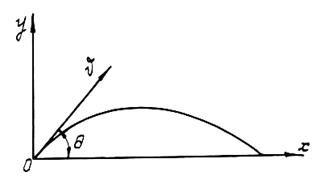
Рис.8
Формула (6.28) дает хорошее совпадение с опытом лишь при напорах истечения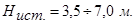 
На дальность боя и высоту подъема струи оказывают влияние сопротивление воздуха и ветер. При этом на дальность боя ветер влияет больше, чем на высоту подъема.
Свободная незатопленная вертикальная струя, покидающая насадок со скоростью 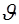, направленной вертикально вверх, теоретически поднимается, как это следует из формулы (6.25), на высоту 
:
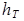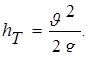
Глава седьмая
Дата: 2019-11-01, просмотров: 228.
