Из формулы потерь напора по длине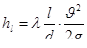 
при турбулентном режиме движения жидкости можно получить выражение для средней скорости при напорном равномерном движении жидкости.
Преобразуем эту формулу, учитывая, что d =4 R :
откуда
.
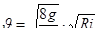Обозначим
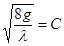. (7.1)
Тогда
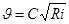, (7.2)
или
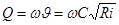. (7.3)
Формула (7.2) так же, как и (7.3), называется формулой Шези.
Эта формула широко применяется в гидротехнической практике для расчета средней скорости потока в каналах, лотках, реках и безнапорных трубах.
Коэффициент с в формуле Шези имеет размерность корня квадратного из ускорения, что непосредственно следует из уравнения (7.1).
В практике расчетов величину с при квадратичной области сопротивления принято определять по эмпирическим и полуэмпирическим формулам. Среди эмпирических формул наибольшее распространение получила формула Н.Н Павловского
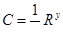, (7.4)
где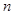 
–коэффициент шероховатости русла, зависящий от материала стенок и их состояния; 
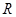–гидравлический радиус, м. 
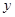–показатель степени, зависящий от 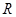и .
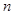Н.Н. Павловский считает возможным применять формулу (7.4) пр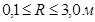и 
и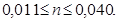 
Из формулы Шези можно получить ряд зависимостей, которые широко применяются при гидравлических расчетах как напорных, так и безнапорных трубопроводов и открытых русл.
Разделив формулы (7.2) и (7.3) на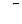 
, получим соответственно
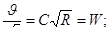(7.5)
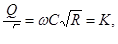(7.6)
откуда следует
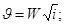(7.7)
(7.8)
Здесь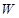 
–модуль скорости (расходная характеристика); 
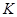– модуль расхода (расходная характеристика).
Решив формулы (7.2) и (7.3) относительно уклона I, получим
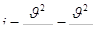; (7.9)
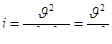. (7.10)
Умножив выражения (7.6) и (7.7) на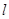 
, найдем
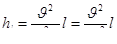; (7.11)
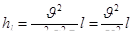. (7.12)
Обозначив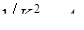 
получим
, (7.13)
или
,
где величина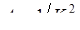 
, равная потере напора на единицу длины трубопровода, при расходе, равном единице, носит название удельного сопротивления трубопровода.
Формулу (7.13) можно записать в виде
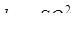, (7.14)
где S –сопротивление трубопровода.
Величины К, А, и S представляют собой обобщенные гидравлические параметры трубопровода, использование которых значительно ускоряет гидравлический расчет.
Зависимости (7.8), (7.12), (7.13) и (7.14) являются основными расчетными формулами простого трубопровода при равномерном движении жидкости.
Если область сопротивления будет отличаться от квадратичной, фактическое значение расходной характеристики К определяется по следующему выражению:
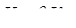, (7.15)
где
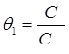. (7.16)
Значения коэффициента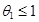 
, полученные Ф. А. Шевелевым для основных видов водопроводных труб, приводятся в справочной литературе.
С учетом (7.15) расчетные зависимости (7.8) и (7.12) примут вид
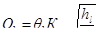(7.17)
и
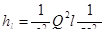. (7.18)
Формулу (7.18) можно также представить в виде
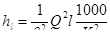, (7.19)
где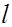 
–длина трубопровода, км, а значение 
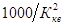приводится также в справочной литературе.
7.2. Гидравлические характеристики трубопроводов
При гидравлическом расчете трубопроводов используются графические методы расчета, в основе которых лежит построение так называемых гидравлических характеристик трубопровода.
Функциональная зависимость потерь напора от расхода h=f(Q) может быть изображена графически (рис.1). Для этого достаточно, задаваясь различными значениями расхода Q, вычислить соответствующие этим значениям потери и напора h по одной из расчетных формул простого трубопровода.
Кривая на рис.1, графически отображающая изменение потерь напора в данном трубопроводе от величины пропускаемого им расхода, называется характеристической кривой, или гидравлической характеристикой трубопровода.
Рассмотрим построение суммарных гидравлических характеристик: а)для простого трубопровода, составленного из труб разного диаметра; б)сложного трубопровода, состоящего из нескольких трубопроводов, соединенных параллельно.
В случае последовательного соединения трубопроводов (см.рис.4) на одном графике строят характеристики отдельных последовательно включенных участков трубопровода.
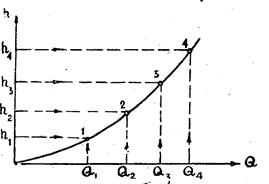
Рис.1
Эти кривые приведены на рис.2, где кривая I –гидравлическая характеристика первого участка с диаметром d1, кривая II –характеристика второго участка с диаметром d2, кривая III –характеристика третьего участка с диаметром d 3.
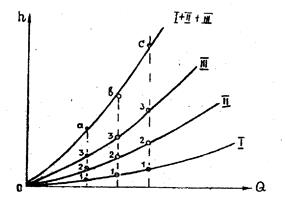
Рис.2
Из ранееизложенного известно, что при последовательном соединении суммируются потери напора. Для построения суммарной гидравлической характеристики всего трубопровода необходимо сложить характеристики отдельных участков по вертикали. Для этого проведем ряд вертикальных прямых, параллельных оси ординат, каждая из которых пересечет все три кривые в точках 1, 2, 3, и сложим при постоянных абсциссах ординаты точек пересечения этих прямых с кривыми.
В результате мы получим ряд точек: а, b, с,..., принадлежащих новой кривой I+II+III, которая и представляет собой искомую суммарную характеристику всего трубопровода.
При параллельном соединении также надо прежде всего построить гидравлические характеристики отдельных параллельно включенных участков (кривые I, II, III на рис.4).
При параллельном соединении общий расход определяется как сумма расходов в отдельных параллельных участках; потери напора в этих участках одинаковы по величине и полная потеря напора определяется как потеря в одном из них.
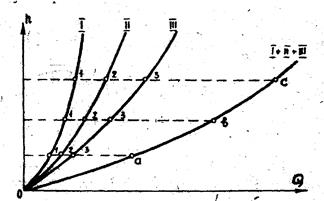
Рис.4
Исходя из этого проводим ряд горизонтальных прямых параллельно оси абсцисс и складываем при постоянных ординатах абсциссы точек их пересечения с характеристиками отдельных участков. В результате сложения получим ряд точек а, в, с..., определяющих суммарную характеристику I+II+III трубопровода три параллельном соединении.
Изложенный метод построения гидравлических характеристик трубопроводов справедлив также и для ламинарного режима, при котором потеря напора графически будет изображаться гидравлическими характеристиками в виде прямых линий с уравнением h=S'Q.
7.3. Понятие о длинных и коротких трубопроводах
При гидравлическом расчете напорные трубопроводы разделяются на длинные и короткие.
К длинным трубопроводам относятся трубопроводы, в которых местные потери напора пренебрежимо малы по сравнению с потерями напора по длине.
При гидравлическом расчете таких трубопроводов местными потерями напора или пренебрегают вовсе, считая, что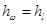 
, или принимают их ориентировочно в размере 5-10% от потерь напора по длине, то есть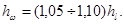 
К коротким трубопроводам относятся трубопроводы небольшой длины, например всасывающие трубы насосных станций и сифоны. В этих трубопроводах местные потери напора являются величинами одного порядка с потерями напора по длине. Поэтому при гидравлическом расчете коротких трубопроводов вычисляются потери отдельно для каждого местного сопротивления.
Длинные напорные трубопроводы подразделяются на простые и сложные. Простым считается трубопровод постоянного или переменного диаметра без ответвлений (рис.5а,б). Сложным является трубопровод постоянного или переменного диаметра, имеющий одно или несколько ответвлений. Сложные трубопроводы, в свою очередь, подразделяются на незамкнутые (тупиковые), рис.6а и на замкнутые (кольцевые), рис.6 б,в.
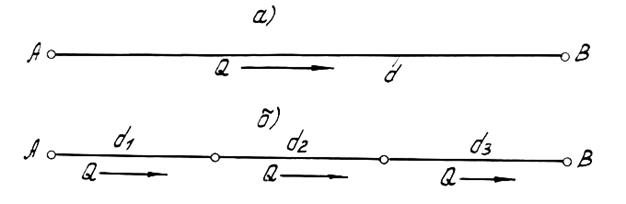
Рис.5
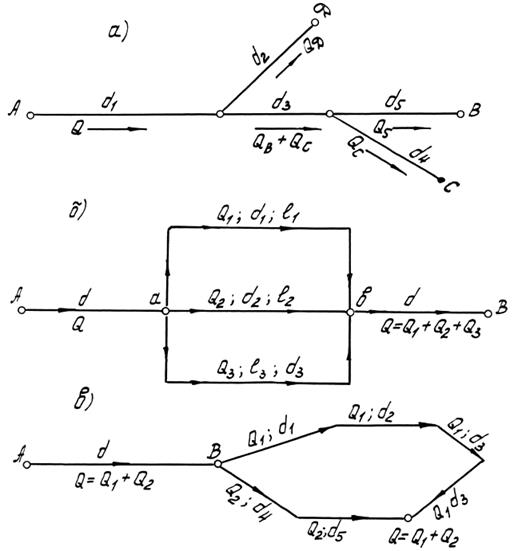
Рис.6
7.4 Гидравлический расчет простого короткого трубопровода
Исходными уравнениями для гидравлического расчета являются уравнение Бернулли и уравнение неразрывности. Рассмотрим истечение жидкости из простого короткого трубопровода в атмосферу. Напишем уравнение Бернулли для сечения 1–1 и 2–2 относительно плоскости отсчета 0–0 (рис.7):
.
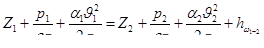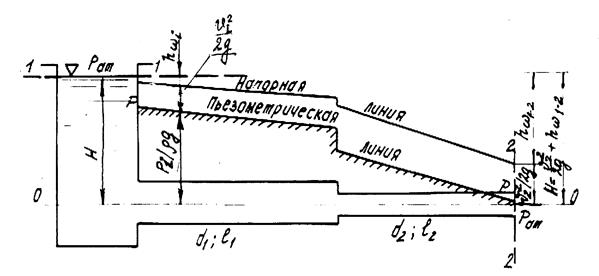
Рис.7
Обозначая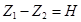 
и учитывая, что 
, 
; 
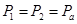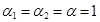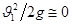, получим:
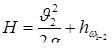, (7.20)
где
.
Таким образом, при истечении жидкости в атмосферу часть действующего напора Н преобразуется в скоростной напор, а часть затрачивается на преодоление гидравлических сопротивлений на участке между рассматриваемыми сечениями 1–1 и 2–2.
Выражая потери по длине и в местных сопротивлениях общими формулами
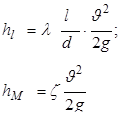
и выражая все потери через скорость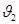 
, получим
.
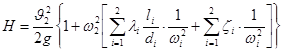Решая это уравнение относительно скорости 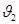, получим:
,
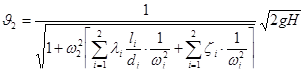а для расхода
,
где
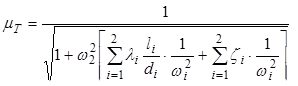
может быть назван коэффициентом расхода трубопровода.
Если участки трубопровода имеют большую длину, то местными потерями или пренебрегают, или учитывают способом эквивалентной длины трубы. Согласно этому способу местные сопротивления с потерей напора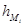 
заменяют в расчете участком трубы длиной 
, выбираемой так, чтобы потеря по длине на ней равнялась бы 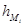. Тогда из условия
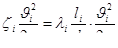
находят эквивалентную длину
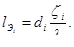
7.5. Основные задачи по расчету простых
Дата: 2019-11-01, просмотров: 255.
