При расчете могут встретиться два случая:
1) расчет новой сети, когда отсутствует заранее заданный напор в начальном пункте ( отметка уровня воды в водонапорной башне);
2) расчет распределительной сети с заданным напором в голове системы, что имеет место при подключении сети к уже имеющемуся водонапорному баку или существующему трубопроводу.
Рассмотрим случай, когда отметка горизонта воды в водонапорной башне неизвестна (рис.11).
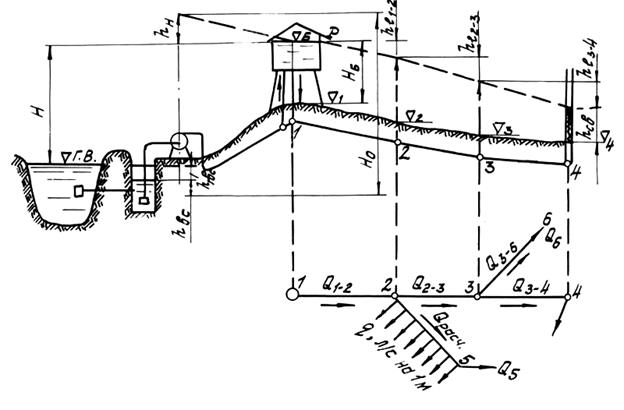 Рис.11
Рис.11
Исходные данные:
а) длины 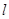 участков сети, их расположение в плане, отметки земли по трассе трубопровода;
участков сети, их расположение в плане, отметки земли по трассе трубопровода;
б) узловые расходы, т.е. расходы, отбираемые в отдельных точках сети ( 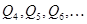 );
);
в) расходы q, отбираемые с 1 м длины того или иного участка сети (в данном случае участка 2-5);
г) свободные напоры 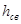 в отдельных точках (узлах) сети, т.е. отсчитываемые от поверхности земли, последние заданы, например,
в отдельных точках (узлах) сети, т.е. отсчитываемые от поверхности земли, последние заданы, например, 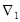 ,
, 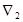 ,
, 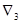 ,
, 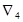 .
.
Задача гидравлического расчета в данном случае:
а) определить диаметры d труб на отдельных участках сети;
б) определить отметку горизонта в водонапорной башне, обеспечивающую подачу требуемых расходов в заданные точки сети.
Порядок расчета
1. Устанавливаем расчетные расходы для отдельных участков сети. Расчетный расход какого-либо участка сети должен равняться сумме расходов, забираемых на сети ниже по течению этого участка. Например, 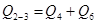 . Расчетный расход для участка 2–5 составляет
. Расчетный расход для участка 2–5 составляет
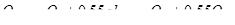 .
.
2. Намечаем в сети линию, которую принимаем за магистральную. Такой линией должна быть линия, по которой пропускается наибольший расход, имеющая наибольшую длину и проходящая по наиболее высоким отметкам поверхности земли. В данном случае это линия 1–2–3–4.
Если в качестве магистральной будет выбрана линия, не отвечающая перечисленным требованиям, то в отдельные конечные точки ответвления не будут поступать требуемые расходы. На это будет указывать то, что в этих конечных пунктах отметки пьезометрической линии будут выше, чем в узлах, расположенных выше (по течению).
3. Рассчитываем магистральную линию, для чего:
а) задаемся для каждого участка магистрали так называемой экономической скоростью 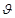 . Величина этой скорости зависит от диаметра труб (чем больше диаметр, тем больше
. Величина этой скорости зависит от диаметра труб (чем больше диаметр, тем больше 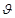 ). Численные значения экономических скоростей для различных диаметров приводятся в справочной литературе, например в таблицах Ф.А. Шевелева или в таблице УП приложения в задачнике по гидравлике А.В. Андреевской, Н.Н. Кременецкого и М.В. Пановой;
). Численные значения экономических скоростей для различных диаметров приводятся в справочной литературе, например в таблицах Ф.А. Шевелева или в таблице УП приложения в задачнике по гидравлике А.В. Андреевской, Н.Н. Кременецкого и М.В. Пановой;
б) задавшись скоростями 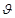 для каждого участка магистрали определяем диаметры труб из соотношения
для каждого участка магистрали определяем диаметры труб из соотношения
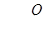 ,
,
где
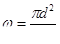 ,
,
откуда
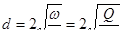 .
.
Найденные значения диаметров округляем до ближайшего (большего или меньшего) стандартного (сортаментного) значения;
в) для полученных значений диаметра, пользуясь таблицей [5], определяем соответствующие значения расходной характеристики К;
г) вычисляем для каждого участка магистрали потери напора по длине 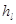 по формуле
по формуле
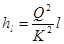 ;
;
д) зная потери напора 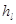 для каждого участка магистрали, строим пьезометрическую линию Р–Р, начиная с конца магистрали, поскольку отметка
для каждого участка магистрали, строим пьезометрическую линию Р–Р, начиная с конца магистрали, поскольку отметка 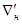 нам задана.
нам задана.
4. Определяем отметку 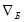 горизонта воды в баке водонапорной башни по формуле
горизонта воды в баке водонапорной башни по формуле
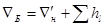 ,
,
где  –суммарные потери напора по длине всей магистрали.
–суммарные потери напора по длине всей магистрали.
Отметка 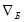 обусловливает высоту водонапорной башни.
обусловливает высоту водонапорной башни.
5. Рассчитываем ответвления. Целью этого расчета является подбор диаметра труб для каждого ответвления, обеспечивающего в конечном пункте свободный напор не меньше требуемого.
Поскольку мы уже построили пьезометрическую линию для магистрали, тем самым мы установили отметки этой линии, т.е. напоры, в начале каждого ответвления, а напоры в концах ответвлений нам заданы.
Порядок расчета ответвлений:
а) вычисляем потери напора по длине 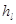 для каждого ответвления по формуле
для каждого ответвления по формуле 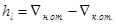 , где
, где 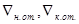 –отметки пьезометрической линии соответственно в начале и конце ответвления;
–отметки пьезометрической линии соответственно в начале и конце ответвления;
б) из формулы для потери напора по длине определяем значения расходной характеристики 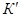 для каждого ответвления
для каждого ответвления
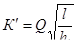 ;
;
в) по таблице для полученных значений 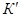 находим соответствующие значения диаметра, причем последние округляются до ближайшего большего стандартного значения;
находим соответствующие значения диаметра, причем последние округляются до ближайшего большего стандартного значения;
г) по найденным округленным значениям диаметра определяем значения расходной характеристики 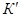 и вычисляем действительные потери напора по длине
и вычисляем действительные потери напора по длине  , после чего уточняем свободные напоры в концах ответвления.
, после чего уточняем свободные напоры в концах ответвления.
7.10. Основы технико-экономического расчета трубопроводов
Из формулы 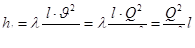 следует, что при заданном расходе жидкости потеря напора по длине трубопровода зависит от диаметра трубы.
следует, что при заданном расходе жидкости потеря напора по длине трубопровода зависит от диаметра трубы.
Увеличение диаметра трубопровода уменьшает потери напора, а следовательно, снижает расход энергии при работе насосной установки. Однако при этом увеличивается стоимость трубопровода (чем больше диаметр, тем больше стоимость).
Учитывая, что устройство длинных напорных трубопроводов связано со значительными капитальными затратами, вопрос о выборе диаметра трубопровода приобретает большое практическое значение и должен решаться с учетом основных факторов, влияющих на стоимость всего сооружения в целом (стоимость трубопровода, насосных установок и других сооружений), а также всех эксплуатационных расходов, связанных с работой насосных установок и самого трубопровода.
Экономически наивыгоднейшим диаметром трубопровода будет такой диаметр, при котором сумма ежегодных денежных затрат (амортизационных и эксплуатационных) по данному комплексу сооружений будет наименьшей.
Задача по определению экономически наивыгоднейшего диаметра трубопровода решается следующим образом: задавшись рядом значений диаметра трубопровода 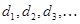 , вычисляют строительную стоимость С всех сооружений в каждом варианте. Затем исходя из расчетного срока окупаемости отдельных сооружений определяют суммарную стоимость всех сооружений в расчете на один год:
, вычисляют строительную стоимость С всех сооружений в каждом варианте. Затем исходя из расчетного срока окупаемости отдельных сооружений определяют суммарную стоимость всех сооружений в расчете на один год:
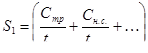 .
.
Подсчитав ежегодные эксплуатационные расходы 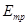 , связанные с работой трубопровода (ремонт, обслуживание), эксплуатационные расходы по насосной станции
, связанные с работой трубопровода (ремонт, обслуживание), эксплуатационные расходы по насосной станции 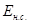 (стоимость энергии, содержание штата, ремонт и т.д.) и другим сооружениям, устанавливают размер полных ежегодных эксплуатационных расходов
(стоимость энергии, содержание штата, ремонт и т.д.) и другим сооружениям, устанавливают размер полных ежегодных эксплуатационных расходов 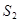 по всему комплексу сооружений:
по всему комплексу сооружений:
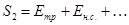
Полная ежегодная стоимость данного варианта трубопровода
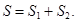
Минимальное значение полной стоимости 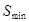 соответствует экономически наивыгоднейшему диаметру трубопровода.
соответствует экономически наивыгоднейшему диаметру трубопровода.
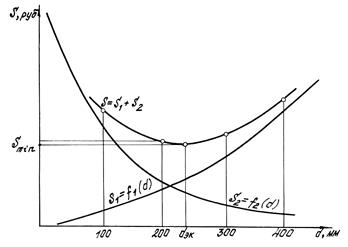
Рис.12
На рис.12 приведен типовой график вида зависимостей
 .
.
Глава восьмая
БЕЗНАПОРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ
8.1 Равномерное движение в открытых каналах
Напомним, что при равномерном движении жидкости средние скорости во всех поперечных сечениях потока равны между собой.
Поэтому равномерное движение жидкости в открытых каналах возможно только в том случае, когда форма и размеры поперечного сечения и уклон дна канала (а также и шероховатость стенок) остаются постоянными па всем его протяжении.
Очевидно, что при этом кривая свободной поверхности жидкости в канале будет параллельна линии дна канала и, следовательно, уклон этой поверхности 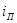 будет равен уклону дна
будет равен уклону дна 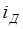 .
.
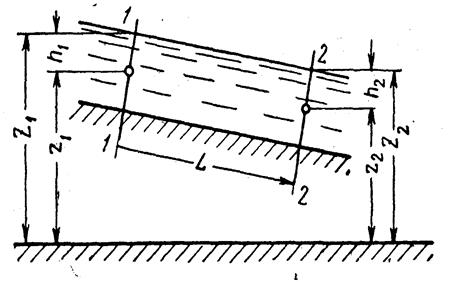
Рис.1
Равномерное движение обычно имеет место, например, в каналах гидростанций, ирригационных и осушительных каналах, трубопроводах, работающих неполным сечением (канализационные трубы, самотечные водоводы), и других потоках со свободной поверхностью.
Рассмотрим сначала движение в открытых каналах. Составим уравнение Бернулли для сечений 1–1 и 2–2 открытого потока (рис.1) при равномерном движении. В общем виде это уравнение имеет вид

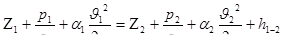 . (8.1)
. (8.1)
Здесь 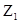 и
и 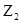 –расстояния до центров тяжести (вертикальные ординаты) сечений 1–1 и 2–2 от некоторой произвольной плоскости сравнения;
–расстояния до центров тяжести (вертикальные ординаты) сечений 1–1 и 2–2 от некоторой произвольной плоскости сравнения; 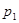 и
и 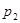 –давления в центрах тяжести названных сечений и
–давления в центрах тяжести названных сечений и 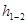 –потеря напора па длине L участка потока между ними.
–потеря напора па длине L участка потока между ними.
Так как в рассматриваемом случае движение равномерное, то
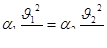
Учтем далее, что 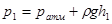 и
и 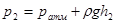 , где
, где 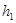 и
и 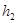 — глубины погружения центров тяжести сечений 1—1 и 2 – 2 под поверхностью жидкости. Поэтому уравнение (8.1) можно переписать следующим образом:
— глубины погружения центров тяжести сечений 1—1 и 2 – 2 под поверхностью жидкости. Поэтому уравнение (8.1) можно переписать следующим образом:
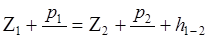 ,
,
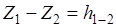 , (8.2)
, (8.2)
где 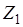 и
и 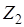 представляют собой расстояния от плоскости сравнения до свободной поверхности жидкости в сечениях 1–1 и 2–2. Представляя потери напора в виде
представляют собой расстояния от плоскости сравнения до свободной поверхности жидкости в сечениях 1–1 и 2–2. Представляя потери напора в виде
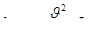 ,
,
вместо уравнения (8.2) получаем
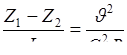 ,
,
откуда
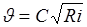 , (8.3)
, (8.3)
где 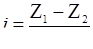 – уклон свободной поверхности, равный при равномерном движении уклону дна потока. Полученная формула (8.3) есть формула Шези, уже рассматривавшаяся ранее, ей часто придают другой вид, обозначая произведение
– уклон свободной поверхности, равный при равномерном движении уклону дна потока. Полученная формула (8.3) есть формула Шези, уже рассматривавшаяся ранее, ей часто придают другой вид, обозначая произведение 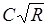 через
через 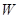
 (так называемая приведенная скорость, или модуль скорости). Тогда
(так называемая приведенная скорость, или модуль скорости). Тогда
 . (8.4)
. (8.4)
Расход жидкости в канале определяется по обычному уравнению расхода
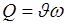 ,
,
или
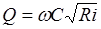 , (8.5)
, (8.5)
и
 , (8.6)
, (8.6)
где
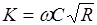 (8.7)
(8.7)
носит название пропускной способности, или модуля расхода.
Приведенная скорость W и пропускная способность К для данного канала могут быть вычислены предварительно по известным размерам, форме сечения и шероховатости стенок канала, что значительно облегчает решение различных практических задач (при этом следует иметь в виду, что, так как гидравлический уклон i –число безразмерное, W и К имеют соответственно те же размерности, что 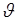 и Q , т. е. измеряются в м/с и м3/с).
и Q , т. е. измеряются в м/с и м3/с).
При расчетах открытых каналов для определения коэффициента С (изменяющегося, как указывалось ранее, в зависимости от размеров и формы сечения канала и шероховатости его стенок) часто применяются, формула Маннинга
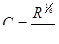 , (8.8)
, (8.8)
формула Н. Н. Павловского
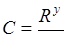 , (8.9)
, (8.9)
а также формула И. И. Агроскина
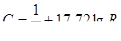 . (8.10)
. (8.10)
где п — коэффициент шероховатости, имеющий те же значения, что и в формуле Маннинга .
Следует иметь в виду, что приведенные формулы (8.8)–(8.10) применимы лишь, для квадратичной области турбулентного режима, что практически обычно имеет место при движении в каналах воды.
В случае безнапорного движения в доквадратичной области турбулентного режима с известным приближением можно пользоваться соотношением
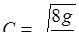 ,
,
определяя коэффициент 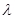 по соответствующим этой области формулам, после замены в них
по соответствующим этой области формулам, после замены в них 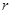 или
или 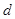 гидравлическим радиусом сечения
гидравлическим радиусом сечения 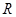 . Более общий характер имеет обобщенная формула А.Д. Альтшуля, действительная для всей области турбулентного режима:
. Более общий характер имеет обобщенная формула А.Д. Альтшуля, действительная для всей области турбулентного режима:
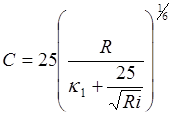 . (8.11)
. (8.11)
При больших уклонах и значительных шероховатостях эта формула упрощается и приводится к виду
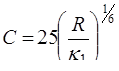 . (8.12)
. (8.12)
Для расчетов безнапорного движения в области ламинарного режима применяются специальные формулы.
8.2. Гидравлические расчеты открытых каналов
При гидравлическом расчете открытых каналов встречаются задачи следующих основных типов:
1. определение расхода жидкости, пропускаемой данным каналом;
2. определение уклона дна, необходимого для пропуска заданного расхода жидкости в канале заданной формы сечения с известной глубиной наполнения;
3. определение глубины наполнения или ширины канала для пропуска данного расхода жидкости при известном уклоне дна.
При решении указанных задач будем исходить из формулы Шези (8.3)
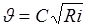 .
.
Подставив в нее значение коэффициента С в его выражении например по Маннингу, получим
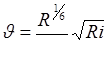 . (8.13)
. (8.13)
При этом для расхода будем иметь следующее выражение:
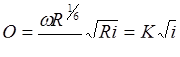 . (8.14)
. (8.14)
Значение площади живого сечения 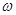 и гидравлического радиуса R в этой формуле зависят от глубины наполнения канала h и от формы его поперечного сечения, коэффициент же шероховатости
и гидравлического радиуса R в этой формуле зависят от глубины наполнения канала h и от формы его поперечного сечения, коэффициент же шероховатости 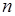 является заданной величиной.
является заданной величиной.
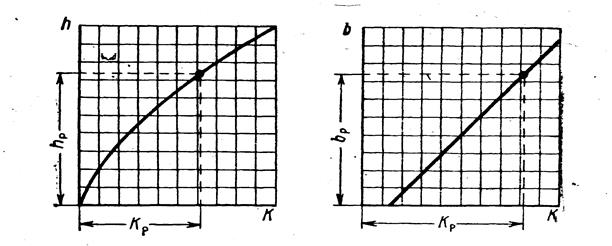
Рис.2 Рис.3
Если заданы форма поперечного сечения канала и глубина его наполнения, находят модуль расхода
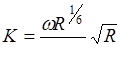 .
.
После этого по формуле (8.14) определяют расход для заданного уклона или уклон, необходимый для пропуска заданного расхода.
Если же известны расход и уклон канала и требуется определить глубину его наполнения, поступают следующим образом: задаются формой поперечного сечения канала и несколькими значениями глубины его наполнения h . Далее вычисляют соответствующие этим наполнениям значения модуля расхода К и строят кривую для К в зависимости от h (рис. 2). Затем откладывают по оси абсцисс значение модуля Кр (соответствующее заданному расходу) и по кривой определяют искомую глубину наполнения hp . В этом случае, когда известна глубина наполнения и необходимо найти ширину канала, поступают аналогично предыдущему –строят график изменения модуля расхода К в зависимости от ширины b и находят по этому графику искомую ширину канала 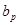 (рис. 3).
(рис. 3).
Подобные задачи могут быть решены также и аналитически, если предварительно выразить через глубину наполнения h величины 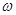 и
и 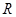 . Так, в случае прямоугольного сечения шириною В имеем
. Так, в случае прямоугольного сечения шириною В имеем
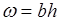
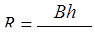 .
.
При трапецеидальном русле (рис.4)
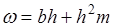
и
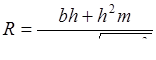 ,
,
где 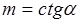
Подставляя эти выражения для 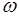 и
и 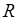 в формулу (8.14), получаем уравнение с одним неизвестным; практически определение глубины h по кривой (описанное выше) оказывается более простым.
в формулу (8.14), получаем уравнение с одним неизвестным; практически определение глубины h по кривой (описанное выше) оказывается более простым.
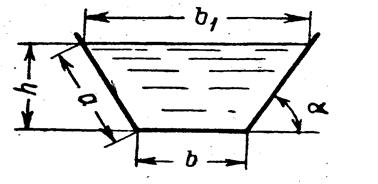
Рис.4
8.3. Допустимые скорости
При больших скоростях движения жидкости в открытых каналах появляется опасность размыва стенок и дна канала. Поэтому скорость приходится ограничивать до определенных предельных значений, устанавливаемых в каждом отдельном случае в зависимости от рода грунта или способа укрепления русла, т.е. от материала стенок и дна канала. В табл.1 приведены примерные значения предельных скоростей для различных грунтов при 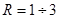 м.
м.
Таблица 1.
| Грунт | Скорость
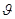 , м/с , м/с
|
| Супесь слабая, пылеватый песок Супесь уплотненная Суглинки легкие (в том числе лессовидные) Суглинки средние Суглинки плотные Глины мягкие Глины нормальные Глины плотные Илистые грунты | 0,7-0,8 1,0 0,7-0,8 1,0 1,1-1,2 0,7 1,2-1,4 1,5-1,8 0,5-0,6 |
Однако при очень малых скоростях взвешенные частицы, (наносы) влекомые потоком (муть, мелкий песок и т. д.), могут выпадать и откладываться на дне канала. Для предотвращения образования осадков на дне капала или, как говорят, заиления канала оказывается необходимым ограничивать также и наименьшую величин средней скорости. Так, средняя скорость для воды, несущей муть должна быть не менее 0,25 м/с, а для воды с мелким песком не менее 0,5 м/с.
Наименьшая допустимая скорость для каналов значительной ширины определяется по эмпирической формуле (8.15), которая может быть представлена также и в более общем виде (8.16):
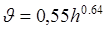 , (8.15)
, (8.15)
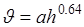 , (8.16)
, (8.16)
В этой формуле h –глубина наполнения капала, 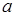 –некоторый коэффициент, значение которого выбирают в зависимости от состава наносов (см.табл.2).
–некоторый коэффициент, значение которого выбирают в зависимости от состава наносов (см.табл.2).
Таблица 2.
| Характеристика наносов | Коэфифциенты |
| Крупные песчано-илистые Средние Мелкие Очень мелкие | 0,60-0,71 0,54-0,57 0,39-0,41 0,34-0,37 |
Для определения величины, пригодная для каналов гидравлически наивыгоднейшего сечения; предельного уклона, при котором может начаться заиление канала, применяется формула
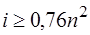 (8.17)
(8.17) 
где п –коэффициент шероховатости по Маннингу.
Необходимо учесть, что ввиду большой сложности указанных явлений приведенные здесь данные следует рассматривать как весьма приближенные, пригодные лишь для ориентировочных (прикидочных) расчетов.
8.4. Движение жидкости в самотечных трубопроводах
К безнапорным (самотечным) трубопроводам относятся канализационные трубы, водосточные каналы (ливнеспуски), самотечные нефтепроводные и водопроводные трубы и т.д.
Наиболее распространенными формами сечений безнапорных трубопроводов являются: круглое (рис.5), овоидальное (рис.5) и лотковое (рис.5). Эти сечения характеризуются интересной гидравлической особенностью: наибольший расход и наибольшая скорость в них имеют место не при полном, а лишь при частичном наполнении.
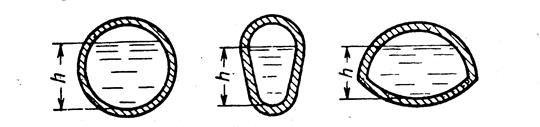
Рис.5
Объясняется это тем, что при заполнении верхней части подобных сечений смоченный периметр растет быстрее, чем площадь, и поэтому начинает уменьшаться гидравлический радиус, что приводит одновременно к уменьшению скорости и расхода.
Гидравлические расчеты безнапорных трубопроводов выполняются аналогично расчетам открытых каналов, что естественно, поскольку безнапорный трубопровод представляет собой по существу также открытый канал; отличием трубопроводов от каналов в гидравлическом смысле является только отмеченное выше уменьшение гидравлического радиуса трубопроводов при заполнении его верхней части, в то время как гидравлический радиус каналом все время возрастает с увеличением наполнения.
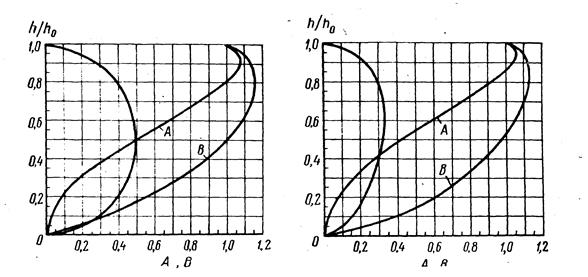
Рис.6 Рис.7
Для упрощения расчетов значения характеристик трубопроводом (площади сечения, гидравлического радиуса и величин 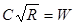 и
и 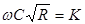 зависящие от глубины наполнения, могут быть вычислены для определенных форм сечения заранее.
зависящие от глубины наполнения, могут быть вычислены для определенных форм сечения заранее.
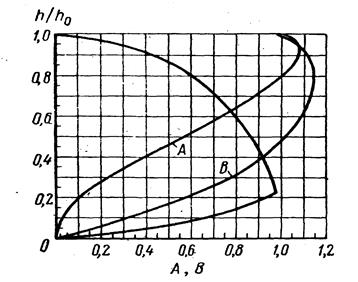
Рис.8
Если обозначить через W 0 и 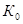 значения модуля скорости и модуля расхода при полном наполнении h 0 трубопровода, а теми же буквами без индекса –их значения при некотором частичном наполнении h , можно вычислить значения отношений
значения модуля скорости и модуля расхода при полном наполнении h 0 трубопровода, а теми же буквами без индекса –их значения при некотором частичном наполнении h , можно вычислить значения отношений
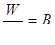 и
и 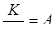
в зависимости от 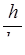 ; получающиеся при этом зависимости для трубопроводов круглого, оваидального и лоткового сечений представлены в виде графиков на рис.6, 7, 8. Пользуясь этими графиками, значения скорости
; получающиеся при этом зависимости для трубопроводов круглого, оваидального и лоткового сечений представлены в виде графиков на рис.6, 7, 8. Пользуясь этими графиками, значения скорости 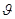 и расхода Q при частичном наполнении можно находить по формулам
и расхода Q при частичном наполнении можно находить по формулам
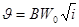 , (8.18)
, (8.18)
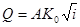 . (8.19)
. (8.19)
8.5. Безнапорное движение при ламинарном режиме
На практике, например при сливе весьма вязких нефтей и нефтепродуктов и их течении в открытых лотках и самотечных трубах, при решении некоторых задач в области химического и нефтезаводского аппаратостроения, иногда приходится встречаться с ламинарным безнапорным движением жидкости.
В этом случае оказывается возможным определить теоретическим путем потери напора (подобно тому, как при ламинарном движении в напорных трубах) и получать расчетные зависимости для расхода. Не приводя здесь соответствующих решений, математически обычно весьма сложных и громоздких, ограничимся лишь сводкой некоторых расчетных формул для каналов наиболее часто применяемых форм поперечных сечении. По И.А.Чарному, для канала прямоугольного сечения при глубине потока h и ширине b расход жидкости может быть подсчитан по формуле
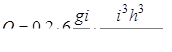 (8.20)
(8.20)
где i –уклон дна канала; g –ускорение силы тяжести; v –кинематическая вязкость жидкости.
Если глубина потока весьма мала по сравнению с шириной, то
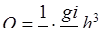 . (8.21)
. (8.21)
Для канала трапецеидальной формы гидравлически наивыгоднейшего сечения с углом 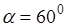
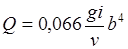 . (8.22)
. (8.22)
Для полукруглого канала
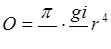 . (8.23)
. (8.23)
Глава девятая
Дата: 2019-11-01, просмотров: 364.