Найдем потери напора на трение при ламинарном движение жидкости в круглой трубе.

С учетом (5.30) можно получить выражение для гидравлического уклона в виде

.

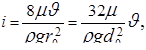
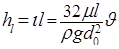Заменяя динамический коэффициент вязкости 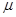 кинематическим 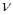, получаем формулу, называемую формулой Пуазейля-Гагена, для потерь напора по длине при ламинарном движении:

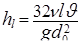.                                (5.31)

Эта формула показывает, что потери напора на трение при ламинарном режиме прямо пропорциональны средней скорости движения. Эти потери не зависят от состояния внутренней поверхности стенок трубы.

Преобразуем формулу (5.31) так, чтобы потери напора 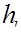 были выражены через скоростной напор :

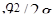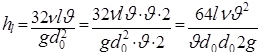.                (5.32)

Сопоставляя формулу (30) с формулой (18), найдем

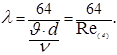                       (5.32)

Полученные зависимости (5.31) и (5.32) с большой точностью подтверждаются опытом только для ламинарных течений в круглых трубах с гладкими стенками. При других режимах коэффициент 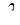 зависит от конфигурации потока и числа Рейнольдса:

.

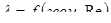 5.7. Структура турбулентного потока

Экспериментальными исследованиями установлено, что при турбулентном режиме движения непосредственно у стенок имеется тонкий ламинарный подслой, далее находится переходный подслой, являющийся переходной зоной от ламинарного движения к турбулентному. Оба подслоя вместе –ламинарный и переходный –составляют пограничный слой. За пределами пограничного слоя располагается ядро течения, в котором движение жидкости является уже турбулентным (рис. 6).

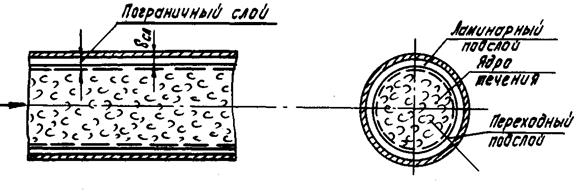
Рис. 6

Исследования также показывают, что скорость в каждой точке турбулентного потока беспорядочно пульсирует около некоторого среднего значения 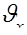 (рис. 7).

Для описания турбулентного потока вместо действительных (мгновенных) значений скорости и давления пользуются осредненными во времени значениями этих величин. Например, осредненное значение продольной составляющей скорости в направлении оси Х в некоторой точке потока определяется соотношением

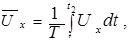                             (5.33)

где 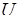 –продольная составляющая мгновенной скорости, зависящая от времени; Т –период осреднения.

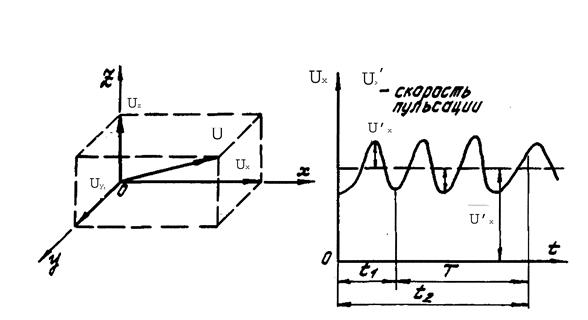
Рис. 7

Действительное значение скорости может быть представлено как сумма осредненной и пульсационной скоростей:

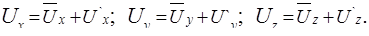   (5.34)

Период осреднения Т должен выбираться достаточно большим по сравнению с периодом пульсаций.

Из равенств (5.34) следует, что осредненные пульсационные скорости должны быть равны нулю. Действительно, подставив под знак интеграла в выражении (5.33) значение 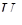, получим

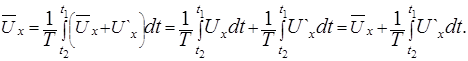(5.35)

Из равенства (5.35) следует, что

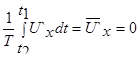.                            (5.36)

Если осредненные величины оказываются для разных последовательных моментов времени постоянными, то такое турбулентное движение считают установившимся.

Уравнение Рейнольдса

Подставив в уравнение Навье-Стокса вместо компонентов скорости их выражения через осредненные и пульсационные величины для установившегося турбулентного движения, получаем уравнения Рейнольдса:

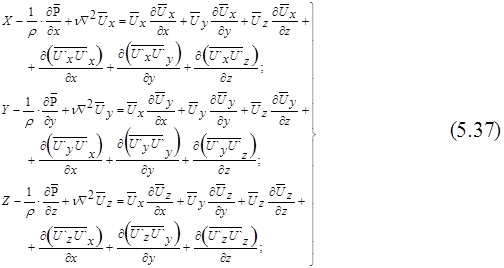
По сравнению с уравнением Навье-Стокса каждое из уравнений движения системы (5.37) включает еще три дополнительных члена, зависящих от пульсаций скорости. Представив каждый из этих членов, например в форме 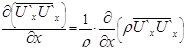, перепишем уравнения Рейнольдса, перенося все члены, зависящие от пульсаций, в левую часть. Для краткости напишем только первое уравнение

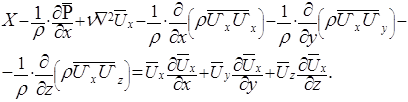
Теперь мы видим, что наряду с членами вида

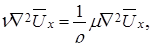
выражающими действие вязкостных напряжений, уравнения Рейнольдса содержат члены вида, которые выражают действие напряжений, присущих только турбулентному потоку:

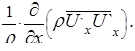
Таким образом, в турбулентном потоке полные касательные напряжения слагаются из вязкостных и турбулентных:

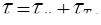                                 (5.38)

причем турбулентные напряжения выражаются формулой и обладают свойством взаимности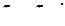

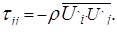
 5.9. Гипотезы Буссинеска и Прандтля

О турбулентных напряжениях

Рассмотрим прямолинейный установившийся турбулентный поток с неравномерным распределением усредненных скоростей (рис. 8).

Одна из существующих гипотез о связи турбулентного напряжения 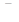 с усредненной скоростью  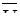заключается в том, что эта связь может быть выражена формулой

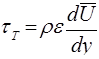.                                (5.39)

Эта формула предложена Буссинеском.

Коэффициент 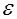, получивший название кинематического коэффициента турбулентной вязкости, имеет размерность 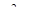. Наиболее простую физическую модель турбулентного потока, позволяющую установить некоторые общие закономерности движения, дает гипотеза Прандтля. Согласно этой гипотезе

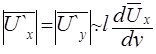                          (5.40)

и, следовательно,

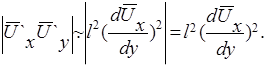
Модуль касательного турбулентного напряжения теперь выражается в виде

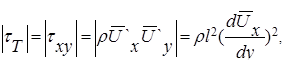                  (40)

где коэффициент 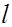, имеющий размерность длины, получил название длины пути перемешивания.

Чтобы пояснить это понятие, допустим, что жидкая частица, имевшая в слое 1 усредненную скорость 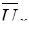 (см. рис. 8), под влиянием турбулентной пульсации  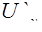перемещается на расстояние 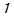, в слой 2, где усредненная скорость равна 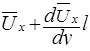. Основное допущение данной теории заключается в том, что путь между слоями 1 и 2 жидкая частица проходит без взаимодействия с другими частицами, т.е. так, как молекула газа проходит путь свободного пробега. Тогда в результате смешения с частицами слоя 2 переместившаяся частица приобретает усредненную скорость этого слоя, т.е. в нем будет иметь место пульсация продольной скорости.

Рис. 8

На рис.8 представлен турбулентный установившийся поток вблизи плоскости стенки.

Используя (5.39) и (5.41), легко установить связь между кинематическим коэффициентом турбулентной вязкости 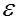 и длиной пути перемешивания :

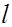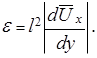                                          (5.42)

Гипотеза Буссинеска, как и гипотеза Прандтля, сводит задачу отыскания связи турбулентных касательных напряжений с полем усредненных скоростей к другой задаче – определению некоторой функции координат 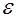 или 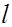, характерной для турбулентного потока.

Решения этой второй задачи основаны или только на экспериментальных данных, или на дополнительных гипотезах. Так, например, Л. Прандтль предположил, что для полубезграничного турбулентного потока вблизи плоской стенки справедлива линейная связь пути перемешивания 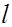 и расстояния от стенки 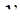: l = ϰy, где ϰ –универсальная постоянная.

 5.10. Турбулентное движение жидкости