При установившемся движении частные производные скорости по времени равны нулю, т.е.

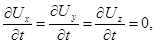
и уравнения (4.17) записываются в виде:

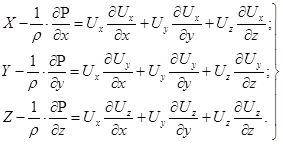              (4.22)

Умножив первое из уравнений (4.22) на проекцию перемещения частицы вдоль элементарной струйки за время dt, т.е. на dx, приведем его к виду

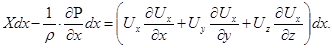       (4.23)

Преобразуем правую часть (4.23) с учетом того, что :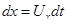

.

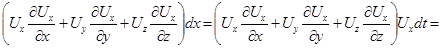
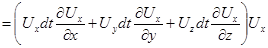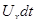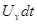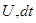Но ,  и  являются проекциями на оси OX , OY и OZ перемещения частицы жидкости вдоль элементарной струйки, т.е. соответственно равны dx , dy и dz, поэтому исследуемое выражение можно представить в виде

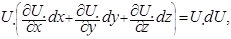
где 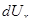 −полный дифференциал компонента  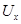скорости частицы, определяемой вдоль элементарной струи.

Если 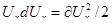, и заменяя на это выражение правую часть уравнения (4.23), получим

.

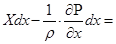
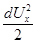Аналогично второе и третье уравнения системы (4.22) можно привести к виду

;

.

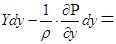
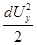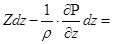
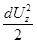Сложим полученные уравнения, группируя слагаемые соответствующим образом, и получим

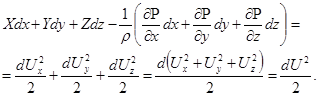
Здесь U −полная скорость в данной точке.

Поскольку, по условию, силы имеют потенциал, то

,

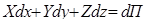где П- силовая функция.

Далее учтем, что при установившемся движении

,

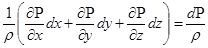и, следовательно,

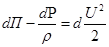.                                    (4.24)

Проинтегрировав уравнение (4.24) вдоль линии тока, получим интеграл Бернулли для установившегося движения в виде

                                (4.25)

Это уравнение пригодно и для трубки тока, если скорости во всех точках сечения одинаковы и зависят только от S. Постоянная в правой части остается таковой вдоль линии тока и меняется при переходе от одной линии тока к другой.

Сравнивая интегралы Эйлера и Бернулли для установившегося движения, можно заметить, что они внешне одинаковы, однако в интеграле Эйлера постоянная одинакова для всего объема жидкости при безвихревом движении, а в интеграле Бернулли- только вдоль лини тока, а движение может быть вихревым.

Если движение происходит под действием силы тяжести, то силовая функция П=- gZ и уравнение (4.25) записываются в виде

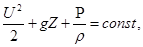                      (4.26)

или, после деления на g,

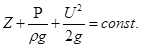                          (4.27)

Это выражение называется уравнением Бернулли для струйки установившегося движения идеальной несжимаемой жидкости.

Здесь Z − геометрическая высота центра тяжести сечения струйки над горизонтальной плоскостью XOY; 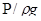 − пьезометрическая высота;  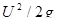− скоростная высота.

 4.8. Геометрическое и энергетическое истолкование

Уравнения Бернулли

Рассмотрим геометрический смысл слагаемых, входящих в уравнение Бернулли.

Напишем уравнение Бернулли для элементарной струйки идеальной жидкости:

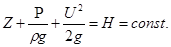
Все слагаемые уравнения имеют размерность длины.

Первый член уравнения Z определят высоту положения центра тяжести рассматриваемого сечения над горизонтальной плоскостью сравнения, его называют геометрической высотой, или геометрическим напором.

Второй член уравнения 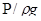 называется пьезометрической высотой, или пьезометрическим напором.

Третий член уравнения 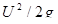называется скоростной высотой, или скоростным напором.

Так как все члены, входящие в уравнение Бернулли, имеют линейную размерность, следовательно, и их сумма, обозначенная через H, также имеет размерность длины. Величину H называют полным (гидродинамическим) напором в данном сечении струйки.

Слагаемые уравнения Бернулли можно изобразить графически, если отнести струйку к системе координат XYZ (рис. 3) и откладывать от горизонтальной плоскости XOY для ряда сечений геометрические напоры Z, пьезометрические − 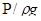 и скоростные −  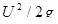высоты. Соединив концы отрезков, выражающих скоростные напоры 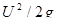, получим горизонтальную линию H - H, расположенную на высоте H от координатной плоскости XOY. Линия H - H называется напорной, или линией полного напора.

Соединив концы отрезков, выражающих пьезометрические высоты 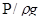, получим линию Р-Р, которая называется пьезометрической. Эта линия изображает изменение суммы геометрической и пьезометрической высот вдоль струйки при движении идеальной жидкости.

Итак, график уравнения дает наглядное представление об изменении всех составляющих полного напора вдоль элементарной струйки при движении идеальной жидкости.

Рассмотрим механический смысл уравнения Бернулли для элементарной струйки идеальной жидкости. Напишем уравнение Бернулли для двух произвольных сечений, например 1-1 и 2-2:

.

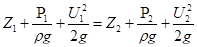Перегруппировав все его члены, этому уравнению можно придать вид:

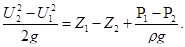                         (4.28)

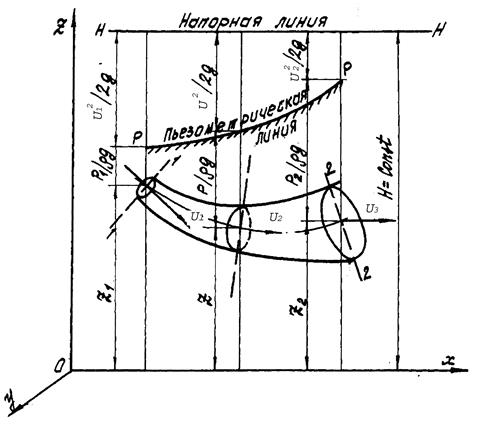
Рис. 3

Получили уравнение кинетической энергии для единицы веса жидкости. Слагаемые в правой части уравнения (4.28) выражают работы удельных сил тяжести и давления, имеют размерность работы. Левая часть уравнения представляет приращение кинетической энергии единицы веса жидкости и также имеет размерность работы. Таким образом, с механической точки зрения слагаемые, входящие в уравнение Бернулли, выражают работу единицы веса жидкости, так как удельные работы можно заменить эквивалентными величинами удельных энергий. Следовательно, можно заключить, что слагаемые, входящие в уравнение Бернулли, выражают удельные энергии струйки, т.е. Z – удельная энергия положения, 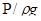 − удельная энергия давления,  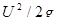− удельная кинетическая энергия и  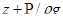− удельная потенциальная энергия.

Из уравнения Бернулли для струйки идеальной жидкости следует, что полная удельная энергия 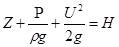 постоянна по длине струйки.

 4.9. Уравнение Д. Бернулли