4.1. Основные дифференциальные уравнения движения
Невязкой жидкости
В потоке жидкости рассмотрим движение элементарного объема в форме параллелепипеда со сторонами dx , dy , dz (рис. 1).
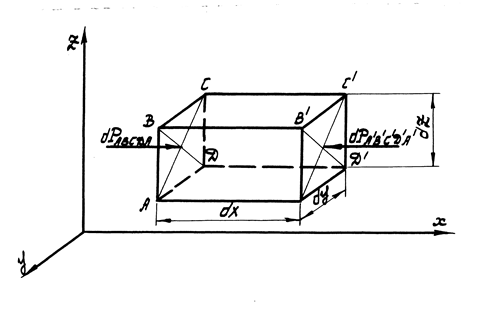
Рис. 1
Напишем второй закон Ньютона для массы жидкости в этом объеме сначала в проекциях на ось Ox:
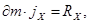(4.1)
где масса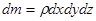 
, а проекция ускорения
.
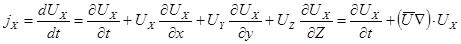Определим проекцию на ось Ox равнодействующих внешних сил. Проекция силы давления на боковую грань АВСД
dP АВСДА = p · dy · dZ ,
где p − среднее давление в пределах указанной грани.
Среднее давление в пределах грани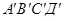 
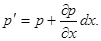
Следовательно, сила давления на эту грань
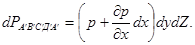
С учетом того что проекция на ось OX силы давления на другие грани параллелепипеда равна нулю, сумма проекций сил давления на боковые грани АВСД и 
будет равна
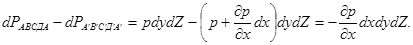
Проекция объемных сил на ось Ox можно представить в виде
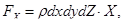
где X –проекция ускорения на ось OX .
Подставляя выражение для проекций сил в формулу (1), получим
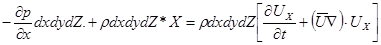
или после сокращения на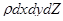 
, т.е. отнеся все члены уравнения к единице массы жидкости в рассматриваемом объеме,
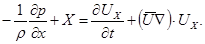
Аналогичные уравнения можно написать и для других координатных осей. В результате получим следующую систему уравнений
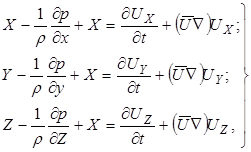(4.2)
которая называется системой уравнений Л.Эйлера для движения сплошной среды.
В систему из трех уравнений входят четыре неизвестные функции:U X , U Y , U Z и p. Поэтому для ее решения необходимо иметь еще одно уравнение, которое связало бы между собой названные функции. Таким уравнением является рассмотренное выше уравнение неразрывности (3.15).
4.2. Дифференциальные уравнения движения
вязкой жидкости (уравнения Навье-Стокса)
Дифференциальные уравнения движения вязкой жидкости могут быть составлены путем дополнения уравнений Л.Эйлера слагаемыми, учитывающими вязкость жидкости. Тогда уравнения Эйлера запишутся в виде
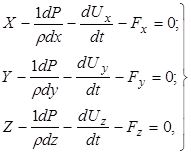(4.3)
где Fx ,Fy, и Fz −проекции сил вязкости, отнесенные к единице массы жидкости, на координатные оси. Найдем силы Fx ,Fy и Fz , предполагая, что жидкость движется слоями, т.е. без перемешивания. Под действием сил вязкости возникают как тангенциальные, так и нормальные напряжения.
Выделим элемент движущейся жидкости в форме параллелепипеда с ребрами, параллельными координатным осям, и определим сумму проекций сил вязкости, действующих только на те три грани параллелепипеда, которые образуют трехгранный угол с вершиной А (рис. 2).
Рис.2
Для удобства дальнейших рассуждений введем двойную индексацию напряжения, например: для нормального напряжения − рхх, касательного напряжения −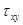 
и т.д. Здесь первый индекс указывает на то, что площадка, для которой определяется напряжение, расположена нормально к данной оси координат, а второй –направление действия напряжения. С учетом этого получим выражение для проекций сил, действующих на грани трехгранного угла с вершиной А:
ось ОХ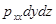 
; 
; 
;
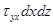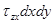ось О Y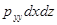 
; 
; 
;
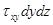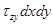ось О Z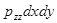 
; 
; 
.
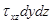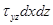Переходя затем к проекциям сил, действующих на грани трехгранного угла с вершиной С, отметим, что напряжения на этих гранях будут отличаться от напряжений на гранях трехгранного угла с вершиной А.
Итак, выражения для проекций сил, действующих на грани трехгранного угла с вершиной С:
ось ОХ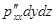 
; 
; 
;
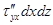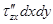ось О Y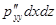 
; 
; 
;
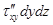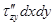ось О Z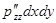 
; 
; 
;
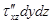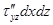где для оси OX
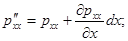
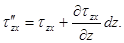
Аналогичные уравнения можно получить и для двух других осей координат.
Составим теперь уравнение для силы, представляющей собой сумму проекций на ось OX сил вязкости.
Полагая, что направление сил, действующих на грани угла с вершиной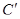 
, противоположно направлению сил, действующих на грани трехгранного угла с вершиной А, получим
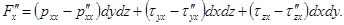
Но
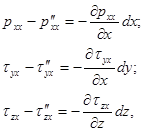
в силу чего, делая соответствующую подстановку, найдем
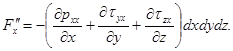
Сила Fx, входящая в уравнение Эйлера, как указано выше, представляет собой проекцию силы вязкости, отнесенной к единице массы жидкости, т.е.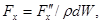 
где в данном случае 
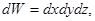а поэтому для силы Fx получим выражение
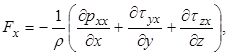(4.4)
где рхх −нормальные,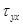 
и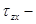 
касательные напряжения.
Касательные напряжения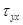 
в пределах грани dxdy остаются одинаковыми для всех ее точек, т.е. не зависят от координат X и Y и изменяются только при перемешивании этой грани вдоль оси OY, т.е. зависят от координаты Y .
Другими словами, 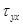−это касательные напряжения, зависящие только от градиента скорости 
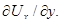Поэтому в соответствии с законом внутреннего трения в жидкости Ньютон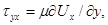а 
а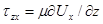 
(по аналогии).
Рассмотрим производную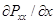 
. Здесь Pxx представляет собой нормальное к площадке dydz напряжение, обусловленное влиянием вязкости (сжатие в условиях торможения и растяжение при ускоренном движении). Поэтому можно допустить, что напряжение Pxx может также определяться по закону Ньютона 
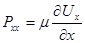, тогда
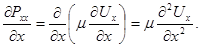
Делая соответствующие подставки в уравнение (4.4), получим
,
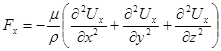или, так как 
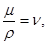
Аналогично для других координатных осей можно записать
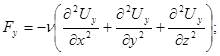
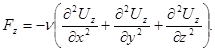
Вводя теперь полученные выражения для сил Fx , Fy , Fz в систему уравнений (4.3), после некоторой перестановки слагаемых получим дифференциальные уравнения движения вязкой жидкости:
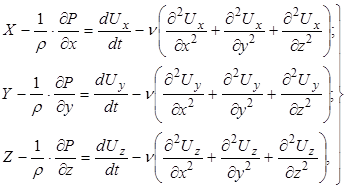(4.5)
или окончательно
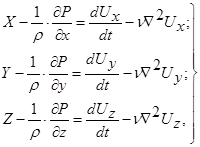(4.6)
где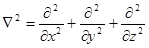 
−оператор Лапласа.
Эти уравнения именуются уравнениями Навье-Стокса. Они составляют основу гидродинамики реальной жидкости.
При решении конкретных задач о движении несжимаемой жидкости к уравнениям Навье-Стокса необходимо добавить уравнение неразрывности в форме
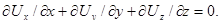
Таким образом, мы получаем замкнутую систему четырех уравнений, достаточную для определения четырех неизвестных величин: трех компонентов скорости Ux , Uy , Uz и давления P.
Кроме того, для определения произвольных постоянных и произвольных функций, появляющихся при интегрировании, должны быть сформулированы так называемые краевые условия, т.е. начальные и граничные условия.
Начальные условия, о которых может идти речь лишь в случае не стационарного движения, указываются посредством задания поля скоростей и давлений в какой-нибудь определенный (начальный) момент времени t = tx.
Задание граничных условий для случая движения вязкости жидкости сводится к признанию того факта, что частицы жидкости, непосредственно соприкасающиеся с поверхностью твердого тела, прилипают к ней и поэтому имеют одинаковую с ней скорость.
В частном случае при обтекании неподвижного тела граничное условие для скорости вязкой жидкости должно быть записано в виде V = 0.
Дифференциальные уравнения движения реальной жидкости представляют собой нелинейные уравнения второй степени в частных производных. В самом общем виде эти уравнения не могут быть проинтегрированы. Их решение возможно лишь для частных случаев, допускающих упрощение этих уравнений путем отбрасывания тех или иных членов. Уравнения движения критериев гидродинамического подобия будут рассмотрены ниже.
4.3. Критерии подобий и моделирование
Гидродинамических процессов
В связи с тем что в большинстве случаев практика решений уравнений Навье-Стокса встречает затруднения, в гидродинамике считают целесообразным прибегать к экспериментированию на моделях. При этом требуется соблюдение одновременного геометрического, кинематического и динамического подобия модели и натурного объекта.
Условимся все величины, относящиеся к модели, обозначать индексом М, а к натуре –Н.
Геометрическое подобие предусматривает пропорциональность сходственных линейных размеров. Если l н –некоторый размер в натуре, а l м−сходственный размер на модели, то при соблюдении геометрического подобия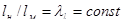 
, где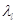 
−геометрический масштаб моделирования. Имея в виду 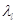, отношение площадей и объемов можно выразить как
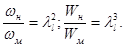
Кинетическое подобие заключается в соблюдении пропорциональности скоростей в сходственных точках натуры и модели в соответствующий момент времени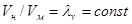 
, где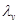 
−кинематический масштаб моделирования. Для кинематически подобных систем соотношение 
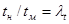также является постоянной величиной. Здесь 
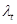−масштаб времени, t н и t м –промежутки времени, в течение которых происходит процесс в натуре и на модели.
Динамическое подобие выражается пропорциональностью векторов сил, действующих в сходственных точках модели и натуры, т.е.
где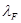 
−масштаб сил. Для всех пар сходственных точек динамически подобных систем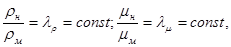 
где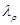 
и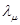 
−соответственно масштабы плотности и вязкости.
Динамически подобные системы могут быть названы механически подобными.
Для получения условий механического подобия применим метод, основанный на анализе дифференциального уравнения движения.
Запишем дифференциальное уравнение движения вязкой жидкости (уравнение Навье-Стокса) для двух сходственных точек натуры и модели:
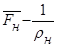
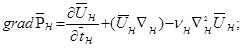(4.7)
; 
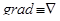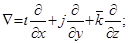
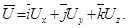
Отнесем все физические величины уравнения (4.7) к соответствующим масштабам и получим выражение
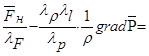
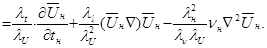(4.8)
Разделив уравнение (4.8) на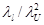 
, получим
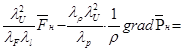
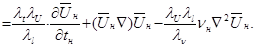(4.9)
Заметим, что для механически подобных систем необходимо, чтобы
движение частиц жидкости в сходственных точках описывалось одинаковыми уравнениями.
Из сопоставления уравнений (4.7) и (4.9) видно, что они будут одинаковыми при равенстве безразмерных множителей в уравнении (4.9) единице, т.е.
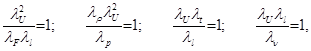
или
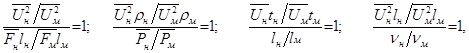
откуда
В общем случае между полученными критериями подобия существует функциональная связь:
(4.10)
При установившемся движении жидкости локальная составляющая инерционной силы в дифференциальном уравнении Навье-Стокса отсутствует и, следовательно, число Струхаля из уравнения (4.9) выпадает, тогда функциональная связь принимает вид
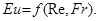(4.11)
Условия моделирования, требующие одновременного соблюдения для натурного объекта и его модели одинаковости критериев Re и Fr не всегда могут быть выполнены:
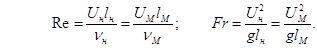
Предположим сначала, что в опытах на модели применяется та же жидкость, что и в натуральном обьекте, так что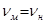 
. Тогда, чтобы удовлетворить условию одинаковости критерия Re, соотношение между скоростями течений в модели и в натурном объекте должно быть равно
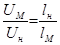, (4.12)
в то время как для соблюдения подобия по критерию Fr необходимо выполнение соотношения
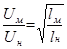. (4.13)
Несовместимость этих двух требований исключает возможность использования для модели жидкости с тем же значением кинематической вязкости, что и в натурном обьекте. Соотношение между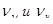 
должно быть определено из критерия Re так, чтобы одновременно было соблюдено соотношение (4.13), вытекающее из критерия Fr.
Находим, что
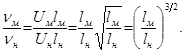
Естественно, что чем меньше будет масштаб модели, тем затруднительнее окажется подбор «модельной» жидкости. Даже при таком, например, сравнительно большом масштабе модели, как ¼ натуральной величины, «модельная» жидкость должна обладать вязкостью в восемь раз меньшей, чем в натурном объекте.
Подбор жидкости со столь отличной вязкостью далеко не всегда оказывается возможным.
В тех случаях, когда строгое моделирование оказывается невыполнимым, прибегают к приближенному моделированию. При этом во внимание принимается лишь один из названных критериев, тот, который для данной задачи имеет наиболее существенное значение.
При больших значениях критерия Рейнольдса, что отвечает значительному преобладанию инерционных сил над силами вязкости, можно в уравнении Навье-Стокса силами вязкости пренебречь. Тем самым критерий Рейнольдса окажется исключением из всех критериев. В таком случае для установившегося движения несжимаемой жидкости (при отсутствии влияния на движение массовых сил) критерий Эйлера Eu становится определяющим:
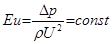. (4.14)
Область значения критерия подобия, в которой он практически перестает быть критерием, называется автомодельной относительно данного критерия.
4.4. Интегралы уравнения движения жидкости
Уравнения Эйлера для общего случая не интегрируются. Интегрирование возможно только в некоторых частных случаях при упрощающих предположениях. В зависимости от принятых допущений различают несколько случаев прямого интегрирования:
1. Интеграл Лагранжа-Коши для безвихревого неустановившегося движения.
2. Интеграл Л. Эйлера для безвихревого установившегося движения.
3. Интеграл Д. Бернулли для установившегося движения вдоль линии тока.
Все интегралы получены при условии, что массовые силы потенциальны.
4.5. Интеграл Лагранжа-Коши
Дата: 2019-11-01, просмотров: 275.
