Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Объем жидкости, протекающей через сечение 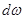 за единицу времени, называют объемным расходом элементарной струйки dQ:

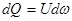.                                          (3.11)

Расход потока жидкости равен алгебраической сумме расходов элементарных струек, составляющих данный поток:

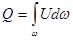.                                          (3.12)

Скорость жидкости U в различных точках поперечного сечения потока, очевидно, может быть неодинаковой, поэтому для характеристики движения всего потока вводится понятие средней скорости потока по сечению (средняя скорость в сечении представляет собой одинаковую для всех точек сечения скорость, при которой проходит тот же расход, какой фактически имеет место при действительных скоростях).

Учитывая, что U = V, получим 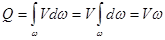, или

,

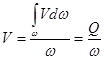из которого следует, что расход потока жидкости равен средней скорости, умноженной на площадь его поперечного сечения:

Q = 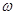V .                                              (3.13)

Живым сечением называют сечение потока с поверхностью, нормальной в каждой своей точке к направлению скорости в этой точке.

Поверхность живого сечения может быть плоской или криволинейной. Величина живого сечения определяется его площадью.

Смоченным периметром называют ту часть полного периметра сечения, по которой жидкость соприкасается с твердыми стенками.

Смоченный периметр обозначают обычно греческой буквой .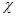

Гидравлическим радиусом называют отношение живого сечения 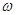 к смоченному периметру, то есть величину

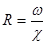.                                               (3.14)

Величина R приближенно характеризует форму и размеры живого сечения.

 

 3.5. Уравнение неразрывности

Внутри движущейся жидкости построим параллелепипед АВСДА₁В₁С₁Д₁ (рис. 4), рассматривая его как некоторое неподвиж­ное относительно координатных осей пространство, через которое протекает жидкость.

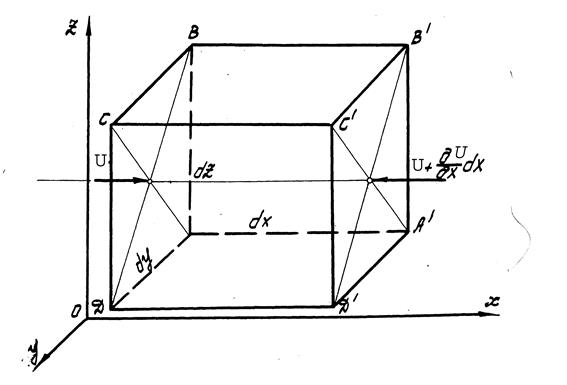
Рис. 4

За время dt через грань АВСДА во внутрь параллелепипеда втекает масса жидкости dM_x , равная

,

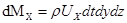а вытекает через грань А₁В₁С₁Д₁ А₁ масса .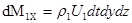

Здесь плотность 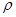 и скорость U на входе в общем случае не равны плотности 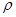₁ и скорости U ₁ на выходе. При этом изменение  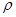и U обусловливается изменением только координаты x, так как втекание и вытекание происходит одновременно. Поэтому

; .

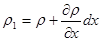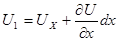следовательно,

.

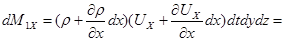
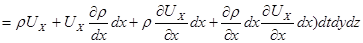Но

,

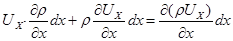а 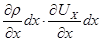 − есть бесконечно малая величина высшего порядка малости относительно других слагаемых и ею можно пренебречь.

Поэтому

.

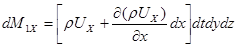Если масса жидкости за время dt внутри параллелепипеда уве­личилась за счет притока на величину dM_X, а уменьшилась за счет вытекания на величину dM _{1 X}, то изменение массы вследствие движения вдоль координатной оси ОХ будет равно:

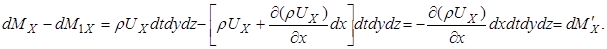Аналогично найдем, что в итоге движения жидкости вдоль осей ОХ и О Z изменение массы за время dt соответственно будет равным:

;

.

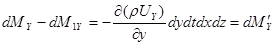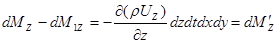Следовательно, общее изменение массы за время dt определяется по формуле:

.

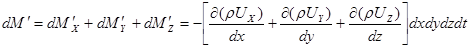Это изменение массы при условии неразрывности движения должно равняться изменению массы, обусловленному изменением плотности. В начальный момент времени t_H масса внутри параллелепипеда

dM_H = 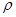dxdydz .

В конечный момент (t + dt) плотность 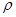 изменяется. Это изменение происходит независимо от координат, поэтому

.

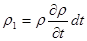Следовательно, в конечный момент времени t_k = t + dt масса жидкости в объеме параллелепипеда

.

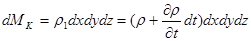Таким образом, приращение массы за время dt находиться по формуле:

.

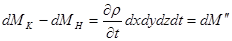При условии неразрывности 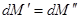, т.е.

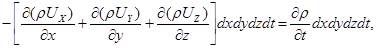
или после сокращения на dxdydzdt

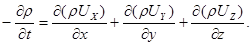                (3.15)

Это и будет искомое уравнение неразрывности. В частном случае –при установившемся движении −плотность 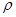 от времени не зависит и .

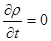Поэтому уравнение неразрывности примет вид

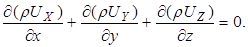                     (3.16)

И, наконец, для несжимаемой жидкости ( 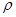= const) уравнение неразрывности примет вид:

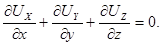                             (3.17)

Посмотрим, каким образом можно интерпретировать принцип сплошности движения применительно к струйке жидкости (см. 3.3 рис.3). Выделим в струйке двумя бесконечно близкими сечениям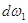и  и 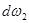, находящимися на расстоянии dS друг от друга, объем

.

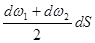Масса жидкости, вошедшая в рассматриваемый объем через сечение 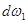, в течение некоторого элементарного промежутка времени dt при расходе в струйке dQ будет равна 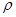dQdt, масса же, вышедшая через противоположное сечение 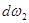, будет равна

.

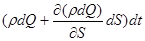Разность между поступающей и вышедшей массой должна, очевидно, равняться изменению за тот же промежуток времени массы 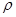d 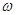dS , первоначально заключавшейся в выделенном объеме, т.е. должна равняться

.

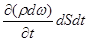Следовательно, имеем равенство

,

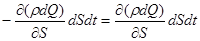откуда

,

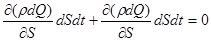или

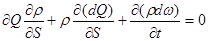.                       (3.18)

В случае мало сжимаемой жидкости изменением плотности 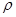 вдоль пути dS можно пренебречь и придать уравнению неразрыв­ности более простое выражение:

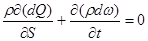.                           (3.19)

Для несжимаемой жидкости ( 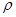 = const) уравнение неразрывности принимает вид

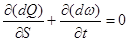.                             (3.20)

В случае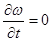

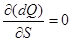,                                   (3.21)

откуда dQ = const или, так как dQ = U ,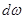

U 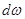 = const .                                  (3.22)

Таким образом, объемный расход жидкости остается неизменным на всем протяжении данной элементарной струйки.

Так как расход потока жидкости равен алгебраической сумме расходов элементарных струек, условие сплошности потока для несжи­маемой жидкости можно записать в виде

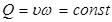.                          (3.23)

 

 3.6. Вихревые и безвихревые движения

Частица жидкости при движении может изменять форму, т.е. де­формироваться. Поэтому движение частицы может быть разложено на поступательное, вращательное и деформационное.

На примере параллелепипеда (рис.5), схематически показаны: поступательное и вращательное; поступательное и деформационное, а также комбинированное (поступательное, вращательное и деформационное движения).

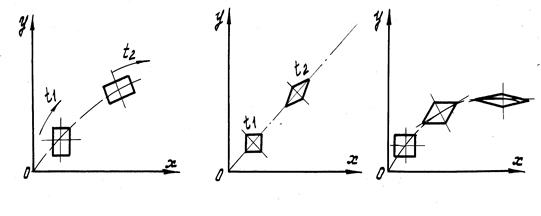
Рис.5

Как видно из схем, вращательное движение характеризуется пово­ротом параллелепипеда вокруг его центра, причем диагонали паралле­лепипеда изменяют свое положение относительно координатных осей. Вращение частицы можно оценивать величиной и направлением угловой скорости при её повороте.

Деформационное движение характеризуется изменением углов между гранями параллелепипеда и оценивается скоростью изменения этих углов.

 3.7 Уравнение компонентов вихря

Вектор 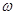 угловой скорости вращения частицы жидкости называется вихрем.

Рассмотрим движение частицы жидкости, имеющей первоначально форму кубика с ребрами, параллельными координатным осям. На (рис.6) этот кубик изображен в проекции на плоскость XOZ квадратом МАСВ.

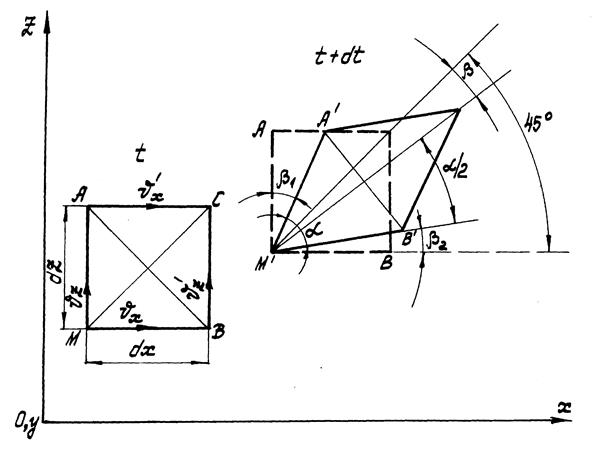
Рис.6

Пусть за время dt кубик переместился и его проекцией стала, фигура 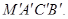 Диагональ МС при этом переместилась в положение 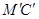, изменив свое начальное направление на угол 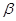. Скорость этого поворота и представляет собой угловую скорость вращения относительно координатной оси Oy, то есть проекцию  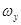вихря.

Найдем выражение угла поворота 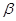. Из (рис.6) следует, что

.

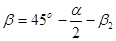Угол 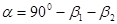, поэтому

.

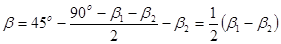Принимая 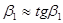 и 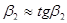  (что допустимо по малости углов), получим

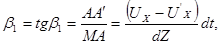
где U _X и 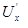− соответственно проекции на ось Ox скоростей точек М и А.

Но 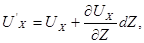 поэтому

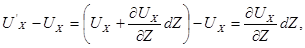
тогда

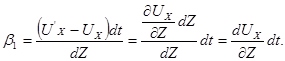
Аналогично получим

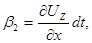
следовательно,

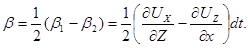
Отсюда компонент вихря – угловая скорость вращения вокруг оси OY

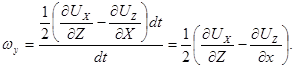
Проводя аналогичные рассуждения по отношению к углам поворота вокруг двух других координатных осей, можно получить следующие выражения для проекций вихря на три оси:

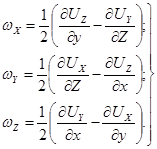                            (3.24)

Величина вихря, т.е. угловая скорость вращения вокруг мгновенной оси,

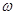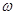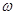Рассмотрим движение при =0 с учетом, что при этом каждый компонент вихря порознь равняется нулю, т.е. _x= _y= 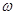_z=0.Такое движение называется безвихревым.

Тогда из (3.24) получается

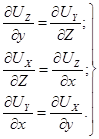                                  (3.25)

Безвихревое движение называют потенциальным (или движение с потенциалом скорости) потому, что при наличие равенства (3.25) существует такая функция 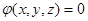, частные производные которой по координатам определяют собой величину проекций скорости. Таким образом,

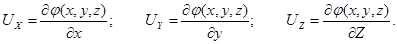      (3.26)

При безвихревом движении функция 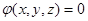 действительно существует.

В самом деле, пусть имеем некоторую функцию 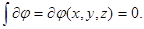 Ее полный дифференциал будет равен

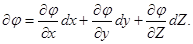
Если существуют равенства (3.26), тогда

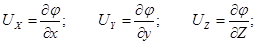
то для полного дифференциала функции 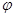 получим

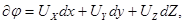                        (3.27)

причем, правая часть уравнения (3.26) должна быть так же полным дифференциалом, а это требует соблюдения равенств (3.25).

Таким образом, если существуют равенства (3.25), то правая часть (3.26) есть полный дифференциал, следовательно, существует функция .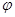

Но эти равенства существуют только при безвихревом движении, следовательно, в этом случае действительно существует и функция 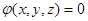, для которой

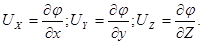
Если для некоторого конкретного случая будет найдена функция 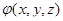, то дальнейшее исследование данного движения уже не встречает затруднений, так как в этом случае путем прямого дифференцирования найденной функции  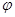можно получить основные уравнения в координатах Эйлера, а именно:

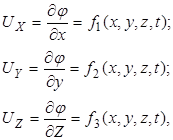
после чего определяются и все иные параметры движения.

Непосредственной подстановкой можно убедиться, что при существовании потенциала скорости уравнение неразрывности (уравнение 3.15) принимает вид

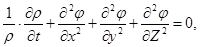
а для случая несжимаемой жидкости (см. уравнение 3.17) оно превращается в уравнение Лапласа:

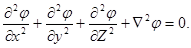
Потенциал скорости 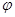, удовлетворяющий этому уравнению, является гармонической функцией.

При изучении потенциальных потоков большое значение имеют эквипотенциальные поверхности, на которых 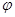=const .

 

 

Глава четвертая