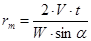Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

, или 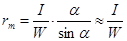.                  (2.43)

где W − объем части тела, погруженной в воду; I − момент инерции плоскости плавания относительно продольной оси; 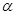 − угол крена; V− объем дополнительно погрузившейся части судна, равный объему обсохшей части судна; t − расстояние по горизонтали от центра тяжести объема V до вертикальной оси плавания.

 

 

Глава третья

 

ГИДРОСТАТИКА.

ОСНОВНЫЕ ПОНЯТИЯ, ОПРЕДЕЛЕНИЯ

И УРАВНЕНИЯ КИНЕМАТИКИ

 3.1. Два метода изучения движения жидкости

Существует два метода изучения движения жидкости: метод Лагранжа и метод Эйлера.

В методе Лагранжа наблюдают за движением каждой отдельной частицы жидкости, исследуя её траекторию. Координаты X ₀ , Y ₀ , Z ₀, соответствующие начальному моменту времени t = t ₀, присва­иваются частице как наименование, позволяющее в любой момент времени отличить её от других частиц.

Положение любой частицы в процессе движения, определяемое значением её радиуса – вектора 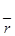 или декартовых координат X , Y , Z, будет функцией её начальных координат (X ₀ , Y ₀ , Z ₀) и времени ( t ):

                                 (3.1)

где X ₀ , Y ₀ , Z ₀ называют переменными Лагранжа.

Чтобы получить скорость определенной частицы и её проекции на координатные оси, следует продифференцировать уравнения (3.1) по времени (t), считая начальные координаты X ₀ , Y ₀ , Z ₀ постоянными:

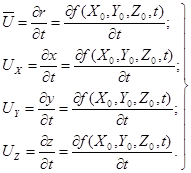                                  (3.2)

Величину ускорения определенной частицы и ее проекции на координатные оси получим, продифференцировав уравнение (3.2) по времени, по-прежнему считая начальные координаты постоянными.

Производная во времени, вычисляемая в переменных Лагранжа, получила название индивидуальной или субстанциональной (поскольку она относится к определенной частице субстанции).

Метод Лагранжа, дающий весьма подробное описание поведения движущейся частицы, не получил, однако, широкого распространения из-за своей громоздкости и сложности:

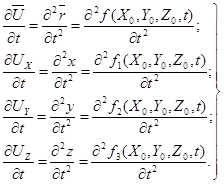                                (3.3)

Для решения большинства практических задач представляет интерес не столько поведение индивидуальной частицы, сколько со­стояние движения в каждый момент времени в каждой точке пространства.

Такое описание движения жидкости проводится при помощи метода Эйлера. В этом методе внимание наблюдателя сосредоточива­ется не на той или иной частице, а на определенной точке пространства, занятого движущейся жидкостью, и исследуется зависимость скорости различных частиц, непрерывно следующих одна за другой через эту точку от координат этой точки X , Y , Z и от времени t:

,

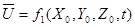или в проекциях на оси координат:

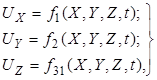                                    (3.4)

где X , Y , Z − называют переменными Эйлера.

Величины X , Y , Z имеют в методах Лагранжа и Эйлера различный смысл. В первом методе эти величины представляют переменные координаты одной и той же движущейся жидкости, во втором являются постоянными координатами одних и тех же точек пространства, через которые в разные моменты времени проходят различные частицы жидкости.

Если в уравнениях (3.4) считать t постоянным, а X , Y , Z переменными, то получим распределение скоростей частиц жид­кости в пространстве для определенного момента времени.

При постоянных значениях X , Y , Z и переменном t получим зависимость скорости жидкости от времени для данной точки пространства, причем в разные моменты времени определяемые значения скорости будут относиться к различным частицам жидкости.

В том случае, когда желательно выяснить, каким образом изменяется скорость с течением времени в данной точке (X , Y , Z) пространства, следует продифференцировать уравнения по време­ни, считая координаты X , Y , Z величинами постоянными.

Если же нас интересует вопрос о том, какое ускорение испытывает определенная частица, проходящая в данный момент времени через точку (X , Y , Z) пространства, то следует рассматривать координаты X , Y , Z как величины переменные, зависящие от времени, ибо за тот бесконечно малый промежуток времени dt ,в течение которого ведется наблюдение за изменением скорости частицы, она успевает перейти из точки (X , Y , Z) в другое положение.

Таким образом, скорость частицы зависит от времени как непосредственно, так и через посредство координат X , Y , Z в свою очередь являющихся функциями времени. Поэтому ускорение частицы следует вычислить, пользуясь уравнением (3.4) по правилу дифференцирования сложной функции:

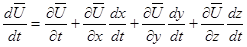.                  (3.5)

Так как

,

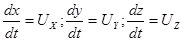имеем

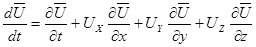.                    (3.6)

Аналогично для компонентов ускорения частицы

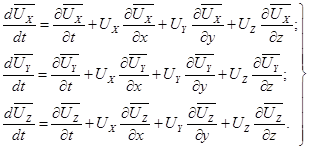                  (3.7)

Первый член правой части уравнения (3.7) 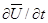  выражает локальное (местное) ускорение частицы. Он характеризует изменение скорости во времени в данной точке пространства, обусловленное нестационарностью скоростного поля. Последующие три члена представляют изменения скорости частицы, обусловленные изменением её координат, и называются конвективными ускорениями.

Вынося из уравнений (3.6) символически за скобку вектор скорости 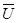, получим

.

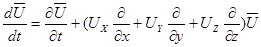Выражение в скобках может быть представлено как скалярное произведение вектора скорости:

,

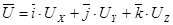на символический вектор 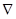 (дифференциальный оператор набла):

,

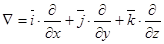и записано в виде

.

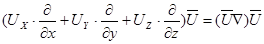Аналогичные преобразования могут быть проведены и в осталь­ных уравнениях (3.7) для компонентов ускорения по координатным осям (X , Y , Z). После этого можно переписать уравнения (3.6) и (3.7) в виде

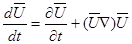;                                     (3.8)

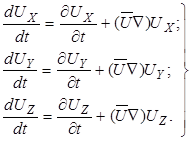                               (3.9)

 

 3.2. Линии тока, трубка тока, траектории и струйка

При анализе движения жидкости методом Эйлера геометрической характеристикой движения служит линия тока. Линия тока −это линия, касательные к которой в любой точке совпадают с направлением вектора скорости частицы жидкости в данной точке. Для её построения выберем в пространстве, занятом движущейся жидкостью, некоторую точку A₁ (рис.1а) и проведем в этой точке отвечающий ей в данный момент времени вектор скорости 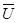₁. Затем возьмем точку А₂, лежащую на векторе 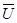₂ вблизи точки A₁, и про­ведем вектор скорости 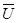₂, относящийся к тому же самому моменту времени, и т.д. Получим ломаную линию А₁А₂А₃….., которая в пределе (при большом количестве точек, бесконечно близких друг к другу) обратится в кривую, которая и будет линией тока. В случае нестационарного потока линии тока отражают мгновенную картину движения жидкости, отвечающую определенному моменту времени. Касательные к линии тока фиксируют направления скорости разных частиц (А_1,А_2,А₃) в последовательных точках пространства в один и тот же момент времени t = t ₁. Касательные к траектории дают направление скорости одной и той же частицы (А₁) в последовательные моменты времени (t _1, t ₂ , t ₃). Траектория частицы А₁ имеет лишь одну общую точку с линией тока, отвечающей моменту времени t = t ₁ (рис.1б).

При стационарном движении линии тока для различных моментов времени совпадают и вместе с тем имеют место их совпадения с траекториями. Это легко понять, если учесть, что каждая частица в любой точке, лежащей на её траектории, имеет то же направление ( и величину ) скорости, что и все остальные частицы, проходящие через эту точку. Действительно, пусть кривая на рис.1 представляет траекторию частицы А₁. В точке I, через которую эта частица проходит в момент времени t ₁ , вектор скорости будет U_{A 1} ( t ₁ ). Но в силу стационарности потока такую же скорость (по величине и направлению) будет иметь и частица A ₂, проходящая через точку I в другой момент времени t ₂, когда частица А₁, следуя вдоль своей траектории, окажется в точке 2. Таким образом, в один и тот же момент времени t ₂ две частицы А₁ и А₂ оказываются на одной и той же траектории, следовательно, эта кривая является одновременно и линией тока.

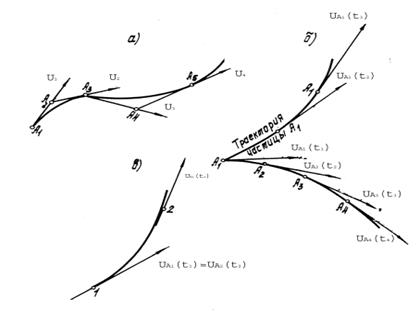
Рис.1

 3.3. Уравнение линии тока

Уравнение линии тока легко составить, пользуясь такими рассуждениями. Допустим, что в данный момент времени имеем плос­кую линию тока а (рис.2).

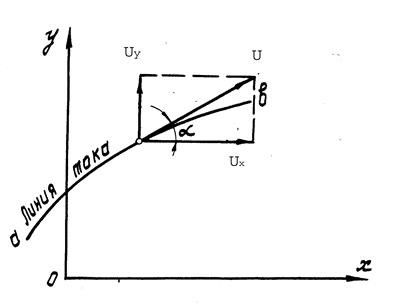
Рис.2

Очевидно, уравнение этой линии можно записать так:

y = f(x),

где x и y − координаты точек данной линии.

Непосредственно из рис.2 имеем U_Y / U_X = tg 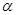, а дифференцируя уравнение линии тока по x, находим

.

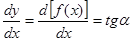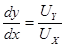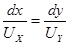Таким образом, , или

, или ,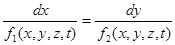

что и является уравнением линии тока в дифференциальном виде.

При пространственном движении дифференциальные уравнения линии тока записываются так: ,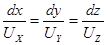

или

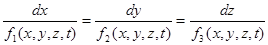.                    (3.10)

Проинтегрировав уравнения (3.10), можно получить уравнение линии тока в конечном виде. Решение этой системы может быть записано в виде двух общих интегралов:

;

,

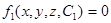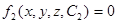где С₁ и С₂ −произвольные постоянные интегрирования.

Каждый из интегралов представляет в геометрическом отношении семейство поверхностей, зависящих от постоянных С₁ и С₂. Линия тока, отвечающая определенным значениям этих постоянных, находится как линия пересечения двух соответствующих поверхностей.

Если внутри движущейся жидкости выделить некоторый замкнутый контур L (рис.3) и через все его точки провести для данного момента времени линии тока, то они образуют поверхность, называемую поверхностью тока. На рис.3 представлена схема струйки в непрерывном потоке.

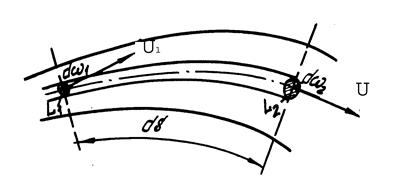
Рис.3

Часть жидкости, ограниченная этой поверхностью, получила название трубки тока.

В нестационарном потоке форма трубок тока непрерывно изменяется, поскольку изменяется направление линии тока. Важнейшим свойством трубки тока является непроницаемость её боковой поверхности для движущихся частиц жидкости, что легко понять, если учесть, что эта поверхность образована линиями тока.

Наряду с трубкой тока в гидродинамике пользуются еще понятием струйки. Струйкой называют часть жидкости, ограниченной поверхностью, образованной совокупностью траекторий, проходящих через все точки замкнутого контура. Для стационарного потока понятия трубки тока и элементарной струйки идентичны, так как линии тока и траекторий в этом случае совпадают.

Струйка имеет малую площадь поперечного сечения 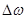 (в пределе 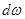), которая может меняться по длине.

Совокупность элементарных струек образует поток жидкости.

 

 3.4. Понятия расхода, средней скорости, живого сечения,