Применяемые в гидравлике
Так как гидравлика изучает законы равновесия и движения жидкостей, логично прежде всего рассмотреть некоторые физические свойства реальных жидкостей. Прежде чем перейти к изучению основных свойств жидкостей, остановимся на единицах измерения, принятых в гидравлике.
За основу принята Международная система единиц измерения (СИ). Кроме того, применяются внесистемные единицы. В инженерной практике используются такие системы МКГСС и СГС.
Основными единицами системы СИ являются:
единица длины – метр (м);
единица массы – килограмм (кг);
единица времени – секунда (с);
единица температуры – градус Кельвина ( К);
единицей силы является Ньютон (Н), т.е. сила, сообщающая массе в 1 кг ускорение в 1 м/с2.
Однако до сих пор в инженерной практике измеряют: давление (напор) в технических атмосферах (атм), метрах водяного столба и миллиметрах ртутного столба (м вод. ст. и мм рт. ст.), температуру в градусах Цельсия(0С), динамическую вязкость в пуазах(Пз) и кинематическую в стоксах (Ст), работу и энергию в киловаттчасах (кВт·ч).
Чтобы оценивать основные физические свойства жидкостей в различных системах единиц измерения, нужно знать соотношения между ними для этих свойств.
В системе СГС за единицу длины принят – см, за единицу времени – с, за единицу массы – г (масса 1 см3 воды при 40С).
Единицей силы в системе СГС служит длина, т.е. сила, которая массе в 1г сообщает ускорение, равное 1 см/с2.
Основные единицы в системе МКГСС:
единица длины – м, единица времени – с, единица силы – килограмм − сила (вес 1 дм3 дистиллированной воды при 40С).
За единицу массы здесь принимается масса, которая под действием силы в 1 кгс получает ускорение, равное 1м/с2. Эту единицу часто называют технической единицей массы (тем).
Назовем некоторые основные соотношения, которые служат для пересчета данных из одной системы единиц в другую
Если принять массу  m=1, ускорение a = 961 см/с2 (ускорение силы тяжести), то получим силу:
m=1, ускорение a = 961 см/с2 (ускорение силы тяжести), то получим силу:
в системе СГС (физической)
Рсгс = 1г · 981 см/с2 = 981 дина;
в системе СИ (международной)
РСИ = 0,001 кг · 9,81 м/с2 = 0,00981 Н;
в системе МКГСС (технической)
РМКГСС = 0,001 кгс.
Отсюда имеем
1Н = 100 000 дин = 0,102 кгс;
1 дина = 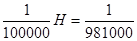 кгс;
кгс;
1 кгс = 9,81 Н = 981 000 дин.
Поступая подобным образом, можно найти также соотношение между единицами измерения массы в различных системах:
1 кг = 1000 г = 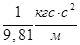 (тем).
(тем).
Размерности и единицы измерения других физических единиц, с которыми приходится иметь дело при гидравлических расчетах, легко получить как производные от установленных выше основных единиц измерения.
1.2. Основные физические свойства жидкостей
Плотность жидкостей
Плотностью жидкости 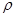 называется ее масса, заключенная в единице объема:
называется ее масса, заключенная в единице объема:
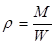 ,
, 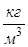 , (1.1)
, (1.1)
где М – масса жидкости; W – объем этой жидкости.
Плотность воды при 40С:
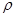 в 40С = 1000
в 40С = 1000 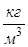 = 102
= 102 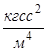 .
.
В практических приложениях о массе жидкости судят по ее весу.
Вес жидкости, приходящийся на единицу объема, называется удельным весом:
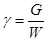 ,
,
где G – вес жидкости; W – объем этой жидкости.
Удельный вес воды при 40С
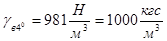 . (1.2)
. (1.2)
Поскольку
G = M · g , (1.3)
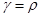 · g , (1.4)
· g , (1.4)
где g – ускорение свободного падения.
Относительным удельным весом жидкости (или относительным весом) 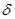 называется отношение удельного веса данной жидкости к удельному весу дистиллированной воды при 40С:
называется отношение удельного веса данной жидкости к удельному весу дистиллированной воды при 40С:
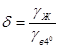 . (1.5)
. (1.5)
Сжимаемость капельных жидкостей под действием давления характеризуется коэффициентом объемного сжатия 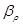 , который представляет собой относительное уменьшение объема жидкости на единицу увеличения напряжения сжатия:
, который представляет собой относительное уменьшение объема жидкости на единицу увеличения напряжения сжатия:
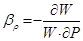 , (1.6)
, (1.6)
где W –первоначальный объем жидкости; 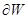 –уменьшение этого объема при увеличении сжимающего напряжения на величину
–уменьшение этого объема при увеличении сжимающего напряжения на величину 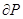 .
.
Коэффициент объемного сжатия в системе СИ имеет размерность 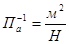 .
.
Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкости:
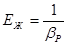 ,
, 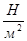 . (1.7)
. (1.7)
Как показывают исследования, при повышении сжимающего напряжения на 9,81 * 104 Па (1 ат) объем воды уменьшается в среднем на 1/20000 часть первоначальной величины.
Для воды
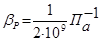 или
или 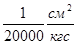 ,
,
ЕВ = 2 · 109 Па.
Вязкость жидкостей
Вязкостью называется свойство жидкостей оказывать сопротивление сдвигу. Все реальные жидкости обладают определенной вязкостью, которая проявляется в виде внутреннего трения при относительном перемещении смежных частиц или слоев жидкости. Таким образом, вязкость характеризует степень текучести жидкости или подвижности ее частиц.
Впервые наличие внутреннего трения в жидкостях было отмечено И. Ньютоном, высказавшем в 1687 г. гипотезу о том, что величина силы внутреннего трения между смежными слоями жидкости зависит от свойств жидкости, пропорциональна площади поверхности соприкасаемых слоев (площади трения) и их относительной скорости перемещения.
Справедливость гипотезы И. Ньютона была доказана русским ученым и инженером Н.П. Петровым в его работе «Трение в машинах и влияние на него смазывающей жидкости», вышедшей в 1883 году. В результате исследования движения жидкости при небольших скоростях в прямолинейной трубе круглого сечения была предложена зависимость
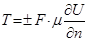 , (1.8)
, (1.8)
или
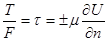 , (1.9)
, (1.9)
где Т – сила внутреннего трения; 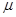 –динамический коэффициент вязкости, т.е. коэффициент, характеризующий сопротивляемость данной жидкости сдвигу. Величина, аналогичная коэффициенту сдвига в твердых телах; F – площадь поверхности соприкасающихся слоев;
–динамический коэффициент вязкости, т.е. коэффициент, характеризующий сопротивляемость данной жидкости сдвигу. Величина, аналогичная коэффициенту сдвига в твердых телах; F – площадь поверхности соприкасающихся слоев; 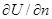 –градиент скорости (относительный сдвиг);
–градиент скорости (относительный сдвиг); 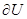 −абсолютный сдвиг (скорость смещения одного слоя относительно другого);
−абсолютный сдвиг (скорость смещения одного слоя относительно другого); 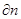 –расстояние между осями двух смежных слоев;
–расстояние между осями двух смежных слоев; 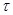 –напряжение сил внутреннего трения, возникающих по поверхности соприкосновения слоев.
–напряжение сил внутреннего трения, возникающих по поверхности соприкосновения слоев.
Знак «+» или «-» принимают в зависимости от знака градиента скорости 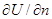 , чтобы
, чтобы 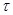 всегда было положительным.
всегда было положительным.
Соотношение 1.8 так же, как и 1.9, называется законом продольного внутреннего трения в жидкостях Ньютона. Поясним этот закон рисунком.
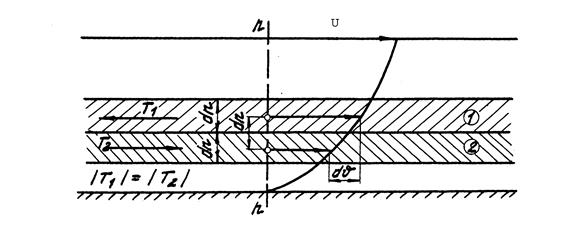
Как видите, трение в жидкости отличается от трения в твердых телах, где сила трения зависит от нормального давления и не зависит от площади трущихся поверхностей и скорости:
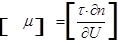 .
.
В системе СИ 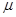 выражается в
выражается в 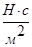 или Па·с.
или Па·с.
В системе МКГСС динамический коэффициент вязкости имеет размерность  .
.
В системе СГС за единицу динамической вязкости принят пуаз (Пз) в честь французского врача Пуазеля, исследовавшего законы движения крови в сосудах человеческого тела, 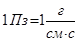 .
.
Соотношение между 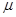 СИ и
СИ и 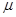 СГС следующее:
СГС следующее:
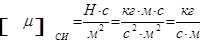 ,
,
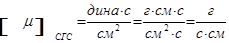 .
.
1Пз = 1 г/см·с = 0,001 кг/0,01 м·с = 0,1 кг/м·с = 0,1 Па · с,
т.е. 1Пз = 0,1 Па·с, 1Пз = 1 дина·с/см2 = 10-5 Н с/10-4м2 = 0,1Н·с/м2 = =0,1 Па·с.
Для пресной воды при t = 100С
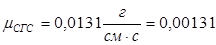 Па·с.
Па·с.
В расчетах часто применяют кинематический коэффициент вязкости 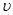 .
.
Связь между 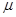 и
и 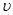 выражается зависимостью:
выражается зависимостью:
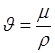 , (1.10)
, (1.10)
где 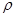 –плотность жидкости.
–плотность жидкости.
Размерность 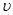 в системе МКГСС – м2/с, в системе СГС – см2/с, в системе СИ –м2/с.
в системе МКГСС – м2/с, в системе СГС – см2/с, в системе СИ –м2/с.
1см2/с = 1 стокс (ст). Для воды при t = 100С
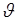 = 0,0131 см2/с = 0,0131 ст = 1,31 сст.
= 0,0131 см2/с = 0,0131 ст = 1,31 сст.
Глава вторая
ГИДРОСТАТИКА
2.1. Силы, действующие в жидкости.
Идеальной жидкости
Умножая уравнения (2.7) соответственно на dx , dy и dz и складывая их, получим
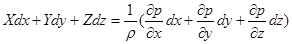 . (2.8)
. (2.8)
Поскольку р = f ( x , y , z ), выражение в скобках в правой части уравнения (2.8) есть полный дифференциал гидростатического давления, следовательно,
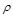 ( Xdx + Ydy + Zdz)= dp . (2.9)
( Xdx + Ydy + Zdz)= dp . (2.9)
Уравнение (2.9) есть основное уравнение гидростатики в дифференциальной форме.
Проинтегрируем уравнение (2.9) для случая, когда жидкость заключена в вертикальном цилиндрическом сосуде и находится в покое под действием силы тяжести и внешнего давления на ее свободной поверхности (рис. 3).
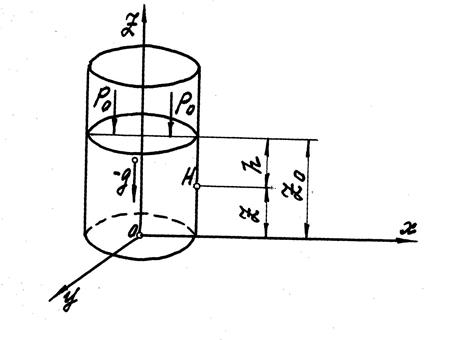
Рис.3
Горизонтальная плоскость XOY называется плоскостью сравнения.
Для рассматриваемого случая, составляющие единичной силы тяжести по координатным осям будут равны:
Х= 0; Y= 0; Z= - g, и отсюда
dp= - 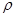 g·dz. (2.10)
g·dz. (2.10)
p= - 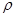 g·Z+C. (2.11)
g·Z+C. (2.11)
При р = р0 и Z = Z 0
C = p0 + 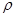 gZ0,
gZ0,
поэтому уравнение (2.11) примет вид
p = - 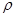 g · Z + р 0 +
g · Z + р 0 + 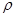 gZ0 , (2.12)
gZ0 , (2.12)
или
p = p0 + 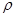 g(Z0 -Z) = p0 +
g(Z0 -Z) = p0 + 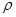 gh, (2.13)
gh, (2.13)
p = p0 + 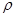 gh, (2.14)
gh, (2.14)
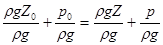 , (2.15)
, (2.15)
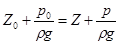 . (2.16)
. (2.16)
Уравнения (2.14) и (2.15) – это две разновидности основного уравнения гидростатики.
Уравнение (2.14) является математическим выражением закона распределения гидростатического давления в жидкости: величина гидравлического давления в некоторой точке, погруженной на глубину h относительно свободной поверхности, равна сумме внешнего давления на свободную поверхность жидкости р0 и давления от веса столба жидкости с площадью основания, равной единице, и высотой, равной глубине погружения h рассматриваемой точки.
Помимо этого уравнение (2.14) показывает, что внешнее давление р0, которое действует на поверхность жидкости, передается всем точкам жидкости без изменения. В этом заключается суть закона Паскаля.
2.4. Полное (абсолютное) и манометрическое давление.
На плоскую стенку
Рассмотрим давление жидкости на плоскую стенку произвольного очертания, наклоненную к горизонту под углом 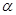 . Давление на поверхности жидкости равно p 0 .
. Давление на поверхности жидкости равно p 0 .
Расположим систему координат так, как показано на рис. 7.
Выделим на смоченной части стенки (на рисунке заштрихована) элементарную площадку 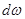 , центр тяжести которой (точка
, центр тяжести которой (точка 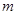 ) погружен под уровень свободной поверхности на глубине h. Абсолютное гидростатическое давление в центре тяжести площадки
) погружен под уровень свободной поверхности на глубине h. Абсолютное гидростатическое давление в центре тяжести площадки 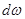 ровно p . Тогда сила гидростатического давления на элементарную площадку
ровно p . Тогда сила гидростатического давления на элементарную площадку 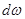 составит
составит
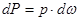 . (2.22)
. (2.22)
Гидростатическое давление согласно уравнению (2.14)
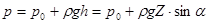 . (2.23)
. (2.23)
Подставляя эти значения p в уравнение (2.22) и интегрируя его, получаем
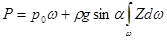 . (2.24)
. (2.24)
Интеграл 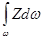 = Sy представляет статистический момент смоченной поверхности стенки
= Sy представляет статистический момент смоченной поверхности стенки 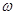 относительно оси Oy.
относительно оси Oy.
Учитывая, что ордината центра тяжести смоченной поверхности равна Zc , глубина его погружения будет 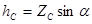 .
.
Тогда статический момент смоченной поверхности относительно оси Oy составит
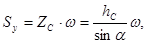 (2.25)
(2.25)
и уравнение (2.24) можно записать в виде
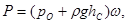
 (2.25)
(2.25)
где 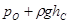 − есть абсолютное гидростатическое давление в центре тяжести смоченной поверхности.
− есть абсолютное гидростатическое давление в центре тяжести смоченной поверхности.
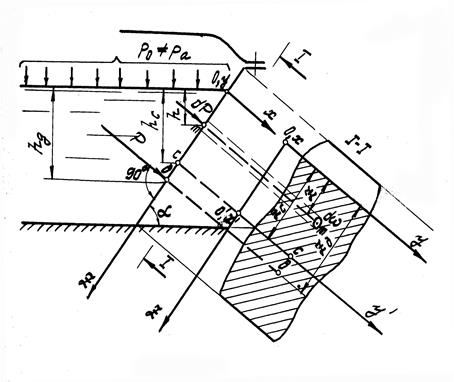
Рис.7
Следовательно, равнодействующая P абсолютного гидростатического давления на плоскую поверхность конечных размеров равна произведению площади смоченной поверхности на абсолютное гидростатическое давление в центре тяжести этой поверхности.
Если p0 равно атмосферному давлению p А, оно уравновешивается таким же давлением на плоскую стенку снизу. В этом случае равнодействующая абсолютного гидростатического давления жидкости будет численно равна силе избыточного (манометрического) давления жидкости на поверхность:
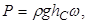 (2.26)
(2.26)
где 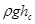 – избыточное (весовое) гидростатическое давление в центре тяжести смоченной поверхности.
– избыточное (весовое) гидростатическое давление в центре тяжести смоченной поверхности.
2.6. Положение центра избыточного давления
Точка приложения силы избыточного гидростатического давления называется центром избыточного давления, или центром давления. Положение центра давления можно определить из условия равенства суммы моментов составляющих силы избыточного давления относительно какой-либо оси моменту равнодействующей силы давления относительно той же оси.
Предположим, что ордината центра давления (ЦД) равна Zg (рис.7). Тогда момент равнодействующей силы давления относительно оси Oy, согласно формуле 2.26,
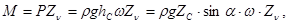 (2.27)
(2.27)
Момент составляющих силы давления относительно той же оси выражается зависимостью:
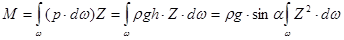 , (2.28)
, (2.28)
где 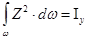 −момент инерции смоченной поверхности
−момент инерции смоченной поверхности 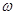 относительно оси Oy.
относительно оси Oy.
Следовательно,
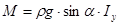 . (2.29)
. (2.29)
Принимая выражения (2.29) и (2.30), получаем
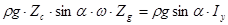 , (2.30)
, (2.30)
откуда
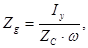 (2.31)
(2.31)
где 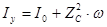 .
.
С учетом этого запишем выражение (32) в таком виде:
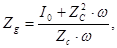
откуда окончательно получим
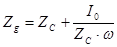 . (2.32)
. (2.32)
2.7. Эпюры гидростатического давления
В ряде случаев для наглядности целесообразно пользоваться диаграммами распределения гидростатического давления по смоченной поверхности. Такие диаграммы называют эпюрами гидростатического давления.
Рассмотрим прямоугольную стенку шириной в, наклоненную под углом 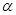 к горизонту. Изобразим эту стенку в аксонометрии (рис.8).
к горизонту. Изобразим эту стенку в аксонометрии (рис.8).
Манометрическое (избыточное) давление р в точке А равно нулю, а в точке В равно 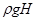 .
.
Поскольку гидростатическое давление всегда нормально к смоченной поверхности стенки, то отрезок, равный 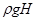 , откладываем на перпендикуляре, восстановленном к стенке в точке В.
, откладываем на перпендикуляре, восстановленном к стенке в точке В.
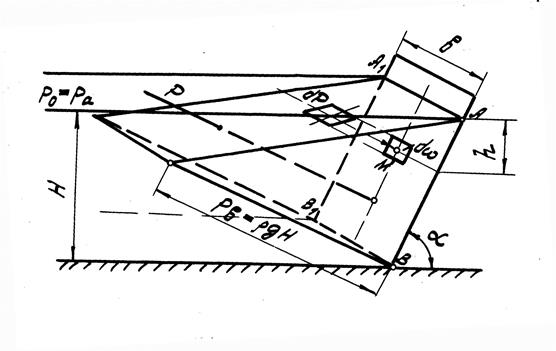 Рис.8
Рис.8
Избыточное гидростатическое давление изменяется пропорционально глубине погружения точки, для которой оно определяется, т.е. по закону прямой линии, поэтому соединим конец отрезка ВС (точку С ) с точкой А прямой. Треугольник ABC будет плоской эпюрой избыточного гидростатического давления. Распределение давления по всей стенке можно представить пространственной эпюрой в виде треугольной призмы ABCC 1 B 1 A 1. Каждая ордината этой призмы представляет в выбранном масштабе избыточное давление в соответствующей точке стенки, а весь объем призмы равен суммарному избыточному давлению жидкости на стенку.
Нетрудно доказать, что линия действия равнодействующей Р сил избыточного гидростатического давления нормальна к стенке ABB 1 A 1 , и проходит через центр тяжести пространственной эпюры, а следовательно, и через центр тяжести плоской эпюры, и встречается со стенкой в центре давления.
С этой целью выделим на плоскости ABB 1 A 1 у точки М элементарную площадку 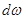 . Избыточное гидростатическое давление в этой точке р =
. Избыточное гидростатическое давление в этой точке р = 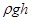 , где h − глубина погружения точки М. Если провести по периметру элементарной площадки нормали, то получим (в пределах эпюры давления) параллелепипед, объем которого р
, где h − глубина погружения точки М. Если провести по периметру элементарной площадки нормали, то получим (в пределах эпюры давления) параллелепипед, объем которого р 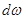 с некоторым приближением можно считать равным элементарной силе dP избыточного давления на площадку
с некоторым приближением можно считать равным элементарной силе dP избыточного давления на площадку 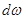 .
.
Если всю эпюру давления разбить на подобные элементарные параллелепипеды, то, очевидно, сумма их объемов будет равна объему всей эпюры, и следовательно, объем эпюры равен равнодействующей всех сил избыточного давления, а линия действия равнодействующей проходит через центр тяжести эпюры.
2.8. Давление жидкости на криволинейные (цилиндрические) (цилиндрические) поверхности
Выделим на некоторой цилиндрической поверхности АВ (рис. 9) элементарную площадку 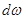 с центром тяжести, погруженным на глубину h под свободную поверхность жидкости. Если давление на поверхности жидкости равно р0, то гидростатическое (абсолютное) давление в центре тяжести площадки составит
с центром тяжести, погруженным на глубину h под свободную поверхность жидкости. Если давление на поверхности жидкости равно р0, то гидростатическое (абсолютное) давление в центре тяжести площадки составит
р=р0 + 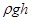 .
.
Тогда d Р − элементарная сила абсолютного гидростатического давления на площадку будет равна
dP = ( p 0 + 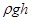 )
) 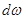 (2.33)
(2.33)
и направлена по нормали к ней, проведенной через центр тяжести.
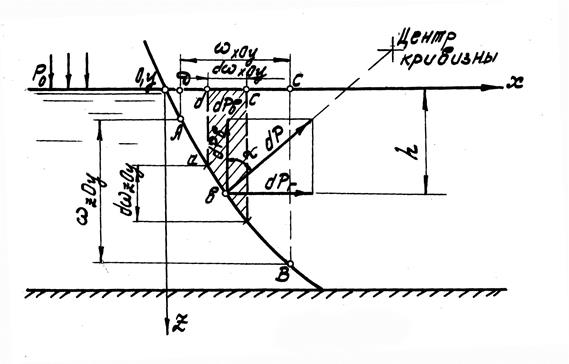
Рис.9
Разложим элементарную силу абсолютного гидростатического давления на вертикальную и горизонтальную составляющие, обозначив угол между элементарной силой dP и вертикалью через 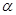 :
:
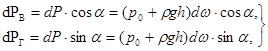 (2.34)
(2.34)
где 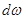 ·cos
·cos 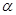 =
= 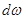 xoy − площадь проекции
xoy − площадь проекции 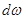 на плоскость XOY;
на плоскость XOY; 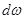 ·sin
·sin 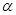 =
= 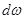 zoy − площадь проекции
zoy − площадь проекции 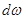 на плоскость ZOY.
на плоскость ZOY.
С учетом приведенных выше равенств уравнение (2.34) можно записать в виде:
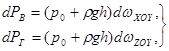 (2.35)
(2.35)
Если всю поверхность АВ разбить на ряд элементарных площадок 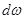 и для каждой из них определить значения dP В и dP Г, то вертикальную РВ и горизонтальную РГ составляющие силы абсолютного гидростатического давления жидкости Р на цилиндрическую поверхность АВ можно найти суммированием всех элементарных сил dP В и dP Г или интегрированием уравнений (2.35):
и для каждой из них определить значения dP В и dP Г, то вертикальную РВ и горизонтальную РГ составляющие силы абсолютного гидростатического давления жидкости Р на цилиндрическую поверхность АВ можно найти суммированием всех элементарных сил dP В и dP Г или интегрированием уравнений (2.35):
 (2.36)
(2.36)
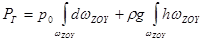 . (2.37)
. (2.37)
Первые интегралы в уравнениях (2.36) и (2.37) равны соответственно площадям проекций цилиндрической поверхности АВ на горизонтальную XOY и вертикальную ZOY плоскости, т.е.
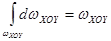 , а
, а 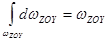 .
.
Проведя вертикальные образующие через различные точки параметра элементарной площадки 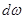 до координатной плоскости XOY, получим некоторый элементарный объем abcd , равный h·
до координатной плоскости XOY, получим некоторый элементарный объем abcd , равный h· 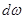 xoy, т.е. объем, записанный под вторым интегралом в уравнении (2.36). Это уравнение теперь можно записать в виде
xoy, т.е. объем, записанный под вторым интегралом в уравнении (2.36). Это уравнение теперь можно записать в виде
РВ=р0 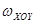 +
+ 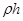 (объем ABC Д). (2.38)
(объем ABC Д). (2.38)
Следовательно, вертикальная составляющая силы абсолютного гидростатического давления равна сумме силы внешнего давления на горизонтальную проекцию цилиндрической поверхности АВ (передающегося от воздействия внешней силы на поверхность жидкости) и веса жидкости в объеме АВСД, ограниченном цилиндрической поверхностью АВ, вертикальными плоскостями АД и ВС свободной поверхности жидкости, а также передней и задней вертикальными плоскостями.
Второй интеграл уравнения (2.37) равен статическому моменту площади проекции цилиндрической поверхности АВ на вертикальную плоскость ZOY относительно оси OY:
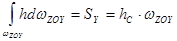 , (2.39)
, (2.39)
где h с − глубина погружения центра тяжести площади 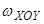 .
.
Из уравнений (2.37) и (2.39) находим
 P Г =(p0+
P Г =(p0+ 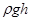 c)·
c)· 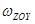 . (2.40)
. (2.40)
Это уравнение идентично уравнению (2.25). Следовательно, горизонтальная составляющая силы полного гидростатического давления на цилиндрическую поверхность АВ равна силе абсолютного гидростатического давления, под воздействием которого находится вертикальная плоская стенка, равная по площади вертикальной проекции цилиндрической поверхности АВ.
Складывая составляющие силы давления РВ и РГ по правилу параллелограмма, получаем силу абсолютного гидростатического давления Р, действующую на цилиндрическую поверхность АВ:
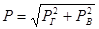 . (2.41)
. (2.41)
Построим эпюру абсолютного гидростатического давления на криволинейную поверхность АВ. Объем АВС1Д1 является эпюрой вертикальной составляющей абсолютного гидростатического давления на рассматриваемую поверхность АВ (рис. 10).
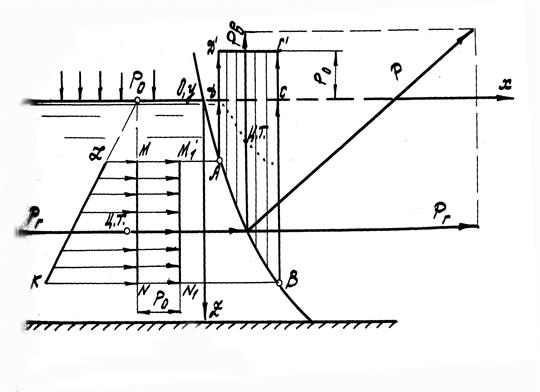
Рис.10
Эту эпюру можно рассматривать как состоящую из двух частей: эпюры АВСД, изобретающей избыточное (весовое) давление на площадь проекции поверхности АВ на плоскость XOY , и эпюры ДСС1Д1, характеризующей внешнее давление р0. Сила давления РВ, равная численно объему АВС1Д1, проходит через центр тяжести этого объема.
Эпюра горизонтальной составляющей абсолютного гидростатического давления на криволинейную поверхность АВ строится так же, как и для плоских стенок. В данном случае она представляется фигурой KZMN , которую можно рассматривать как состоящую из двух частей: эпюры KZM 1 N 1 , изображающей избыточное (весовое) давление жидкости, и эпюры MNN 1 M 1, характеризующей внешнее давление р0. Сила давления Р T , равная объему эпюры KZM 1 N 1 , проходит через центр тяжести этого объема.
2.9. Плавание тел
Закон Архимеда. Открыт за 250 лет до н.э. Характеризует плавучесть тела, погруженного в жидкость. Этот закон гласит: "Результирующая сила давления Р жидкости на погруженное в нее тело равна по величине весу жидкости в объеме погруженного в нее тела и “направлена по вертикали снизу вверх” (рис.11).
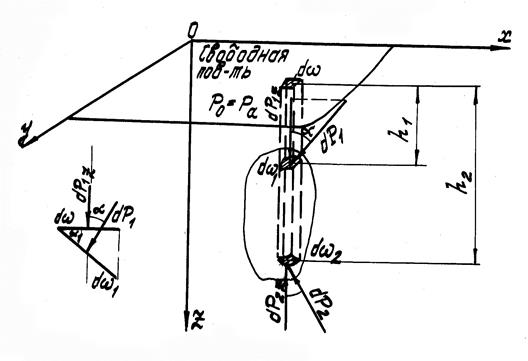
Рис.11
Видно, что 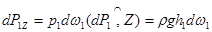 , а
, а
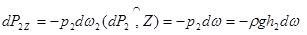 ;
;
dP = dP1Z -dP2Z .
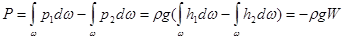 .
.
Знак минус указывает на то, сила P направлена снизу вверх.
Плавучесть тела. Если вес погруженного в жидкость тела G меньше архимедовой силы, т.е. P = 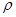 gW > G, тело всплывает. Если Р < G , тело тонет. При P = G =
gW > G, тело всплывает. Если Р < G , тело тонет. При P = G = 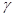 W тело не тонет и не всплывает, находясь в состоянии покоя в любой точке водного пространства.
W тело не тонет и не всплывает, находясь в состоянии покоя в любой точке водного пространства.
Следовательно, когда Р > G, то только часть тела погружена в жидкость, что характеризует его плавучесть. В этом случае архимедова сила Pn равна весу жидкости в объеме погруженной в нее части тела 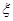 W, где
W, где 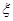 − коэффициент, определяющий часть тела, погруженную в жидкость (
− коэффициент, определяющий часть тела, погруженную в жидкость ( 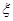 < 1),
< 1),
Pn = 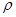 g
g 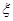 W = Gn . (2.42)
W = Gn . (2.42)
Вес жидкости в объеме погруженной в нее части тела 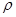 g
g 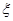 W называется водоизмещением. Центр давления при плавании, т.е. точка приложения архимедовой силы, называется центром водоизмещения. При качке судна центр давления меняет свое положение, т. к. в этом случае одна часть судна погружается в воду, а противоположная, наоборот, выходит из воды. Это меняет форму подводной части судна и, следовательно, положение центра давления. Водоизмещение определяет максимальную величину погружения судна в воду и его грузоподъемность.
W называется водоизмещением. Центр давления при плавании, т.е. точка приложения архимедовой силы, называется центром водоизмещения. При качке судна центр давления меняет свое положение, т. к. в этом случае одна часть судна погружается в воду, а противоположная, наоборот, выходит из воды. Это меняет форму подводной части судна и, следовательно, положение центра давления. Водоизмещение определяет максимальную величину погружения судна в воду и его грузоподъемность.
Водоизмещение некоторых судов и понтонов:
супертанкер "Крым"− 160 000 т (1974 г.),
атомный ледокол "Ленин"− 16000 т,
понтоны для подъемам затонувших судов− от 40 до 400 т.
Линия пересечения свободной поверхности водоема с боковой поверхностью судна при его максимальной нагрузке называется ватерлинией, а плоскость в пределах судна, ограниченная ватерлинией, − плоскостью плавания (рис.12).
Вертикальная ось симметрии 0-0, нормальная к плоскости плавания и обязательно проходящая через центр тяжести с плавающего тела или судна, называется осью плавания. Центр тяжести сухогрузного судна (неналивного) не меняет своего положения при качке. У наливных судов, имеющих свободную поверхность залитой жидкости, центр тяжести при качке перемещается.
Остойчивость плавающего тела. Плавающее тело при качке может наклоняться в ту или другую сторону или, как обычно говорят, давать крен. 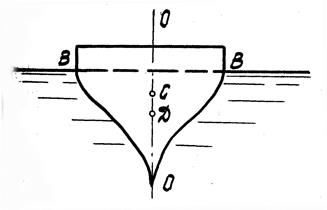 Способность судна возвращаться из крена в первоначальное положение называется остойчивостью судна.
Способность судна возвращаться из крена в первоначальное положение называется остойчивостью судна.
Плавающее тело или судно имеет на оси плавания 0-0 три характерные точки (рис.13): центр тяжести С, центр давления Д и метацентр М. Метацентром называется точка пересечения оси плавания с линией действия архимедовой силы при крене плавающего тела или судна.
Рис.12
Как уже было отмечено, центр давления при крене судна перемещается, поэтому и положение метацентра не может оставаться постоянным. Однако при кренах, не превышающих 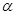 = 15°, положение метацентра почти не меняется и его принимают неизменным. В этом случае центр давления или водоизмещения Д перемещается примерно по дуге (с углом
= 15°, положение метацентра почти не меняется и его принимают неизменным. В этом случае центр давления или водоизмещения Д перемещается примерно по дуге (с углом 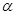 = 15°) окружности радиусом rm, описанной из метацентра М. Радиус rm, называется метацентрическим радиусом.
= 15°) окружности радиусом rm, описанной из метацентра М. Радиус rm, называется метацентрическим радиусом.
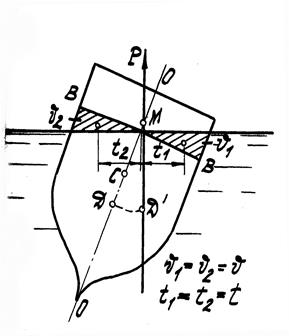 При углах крена
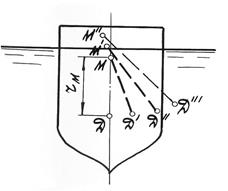
При углах крена 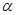 > 15° центр водоизмещения перемещается по некоторой кривой Д' Д" Д"' и т.д., отличной от дуги окружности, и метацентр уже не сохраняет своего постоянного положения (рис.14).
> 15° центр водоизмещения перемещается по некоторой кривой Д' Д" Д"' и т.д., отличной от дуги окружности, и метацентр уже не сохраняет своего постоянного положения (рис.14).
Остойчивость судна зависит от относительного положения центров Д, С и М.
Рассмотрим остойчивость для трех различных случаев относительного Рис.13 положения центров С и М (рис.15).
В случаях а и б судно остойчиво, так как действие пар сил Р и G препятствует крену. В случае же в остойчивость судна не обеспечена (судно опрокинется), т.к. пара сил Р и G увеличивает крен судна.
 Различное влияние этих пар сил на остойчивость плавающих тел зависит от взаимного положения центра тяжести С и метацентра М : если метацентр выше центра тяжести, судно остойчиво, если же метацентр ниже центра тяжести, судно неостойчиво.
Различное влияние этих пар сил на остойчивость плавающих тел зависит от взаимного положения центра тяжести С и метацентра М : если метацентр выше центра тяжести, судно остойчиво, если же метацентр ниже центра тяжести, судно неостойчиво.
Остойчивость можно характеризовать соотношением rm и l: при rm > l судно остойчиво, а при rm < l судно неостойчиво. Заметим, что l > 0 , когда Д ниже С, и l < 0, когда Д выше С. Величина m, выражающая превышение метацентра над центром тяжести (m=rm - l), называется метацентрической высотой.
Рис.14
Для остойчивости судна или тела необходимо, чтобы метацентрическая высота имела положительное значение, т.е., если m > 0 , тело остойчиво, если же m < 0, тело неостойчиво.
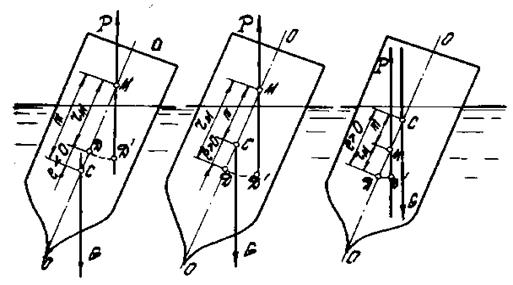
Рис.15
ГИДРОСТАТИКА.
ОСНОВНЫЕ ПОНЯТИЯ, ОПРЕДЕЛЕНИЯ
И УРАВНЕНИЯ КИНЕМАТИКИ
3.1. Два метода изучения движения жидкости
Существует два метода изучения движения жидкости: метод Лагранжа и метод Эйлера.
В методе Лагранжа наблюдают за движением каждой отдельной частицы жидкости, исследуя её траекторию. Координаты X 0 , Y 0 , Z 0, соответствующие начальному моменту времени t = t 0, присваиваются частице как наименование, позволяющее в любой момент времени отличить её от других частиц.
Положение любой частицы в процессе движения, определяемое значением её радиуса – вектора 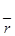 или декартовых координат X , Y , Z, будет функцией её начальных координат (X 0 , Y 0 , Z 0) и времени ( t ):
или декартовых координат X , Y , Z, будет функцией её начальных координат (X 0 , Y 0 , Z 0) и времени ( t ):
 (3.1)
(3.1)
где X 0 , Y 0 , Z 0 называют переменными Лагранжа.
Чтобы получить скорость определенной частицы и её проекции на координатные оси, следует продифференцировать уравнения (3.1) по времени (t), считая начальные координаты X 0 , Y 0 , Z 0 постоянными:
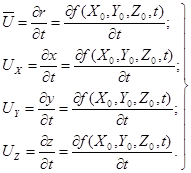 (3.2)
(3.2)
Величину ускорения определенной частицы и ее проекции на координатные оси получим, продифференцировав уравнение (3.2) по времени, по-прежнему считая начальные координаты постоянными.
Производная во времени, вычисляемая в переменных Лагранжа, получила название индивидуальной или субстанциональной (поскольку она относится к определенной частице субстанции).
Метод Лагранжа, дающий весьма подробное описание поведения движущейся частицы, не получил, однако, широкого распространения из-за своей громоздкости и сложности:
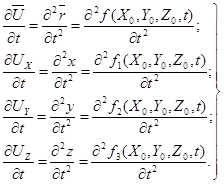 (3.3)
(3.3)
Для решения большинства практических задач представляет интерес не столько поведение индивидуальной частицы, сколько состояние движения в каждый момент времени в каждой точке пространства.
Такое описание движения жидкости проводится при помощи метода Эйлера. В этом методе внимание наблюдателя сосредоточивается не на той или иной частице, а на определенной точке пространства, занятого движущейся жидкостью, и исследуется зависимость скорости различных частиц, непрерывно следующих одна за другой через эту точку от координат этой точки X , Y , Z и от времени t:
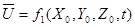 ,
,
или в проекциях на оси координат:
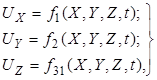 (3.4)
(3.4)
где X , Y , Z − называют переменными Эйлера.
Величины X , Y , Z имеют в методах Лагранжа и Эйлера различный смысл. В первом методе эти величины представляют переменные координаты одной и той же движущейся жидкости, во втором являются постоянными координатами одних и тех же точек пространства, через которые в разные моменты времени проходят различные частицы жидкости.
Если в уравнениях (3.4) считать t постоянным, а X , Y , Z переменными, то получим распределение скоростей частиц жидкости в пространстве для определенного момента времени.
При постоянных значениях X , Y , Z и переменном t получим зависимость скорости жидкости от времени для данной точки пространства, причем в разные моменты времени определяемые значения скорости будут относиться к различным частицам жидкости.
В том случае, когда желательно выяснить, каким образом изменяется скорость с течением времени в данной точке (X , Y , Z) пространства, следует продифференцировать уравнения по времени, считая координаты X , Y , Z величинами постоянными.
Если же нас интересует вопрос о том, какое ускорение испытывает определенная частица, проходящая в данный момент времени через точку (X , Y , Z) пространства, то следует рассматривать координаты X , Y , Z как величины переменные, зависящие от времени, ибо за тот бесконечно малый промежуток времени dt ,в течение которого ведется наблюдение за изменением скорости частицы, она успевает перейти из точки (X , Y , Z) в другое положение.
Таким образом, скорость частицы зависит от времени как непосредственно, так и через посредство координат X , Y , Z в свою очередь являющихся функциями времени. Поэтому ускорение частицы следует вычислить, пользуясь уравнением (3.4) по правилу дифференцирования сложной функции:
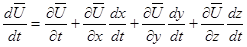 . (3.5)
. (3.5)
Так как
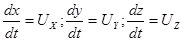 ,
,
имеем
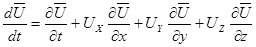 . (3.6)
. (3.6)
Аналогично для компонентов ускорения частицы
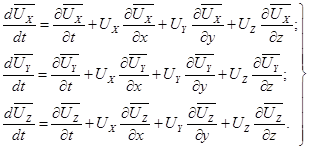 (3.7)
(3.7)
Первый член правой части уравнения (3.7) 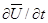 выражает локальное (местное) ускорение частицы. Он характеризует изменение скорости во времени в данной точке пространства, обусловленное нестационарностью скоростного поля. Последующие три члена представляют изменения скорости частицы, обусловленные изменением её координат, и называются конвективными ускорениями.
выражает локальное (местное) ускорение частицы. Он характеризует изменение скорости во времени в данной точке пространства, обусловленное нестационарностью скоростного поля. Последующие три члена представляют изменения скорости частицы, обусловленные изменением её координат, и называются конвективными ускорениями.
Вынося из уравнений (3.6) символически за скобку вектор скорости 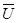 , получим
, получим
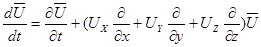 .
.
Выражение в скобках может быть представлено как скалярное произведение вектора скорости:
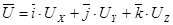 ,
,
на символический вектор 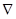 (дифференциальный оператор набла):
(дифференциальный оператор набла):
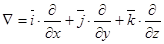 ,
,
и записано в виде
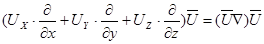 .
.
Аналогичные преобразования могут быть проведены и в остальных уравнениях (3.7) для компонентов ускорения по координатным осям (X , Y , Z). После этого можно переписать уравнения (3.6) и (3.7) в виде
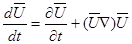 ; (3.8)
; (3.8)
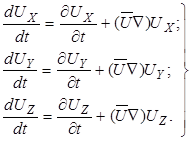 (3.9)
(3.9)
3.2. Линии тока, трубка тока, траектории и струйка
При анализе движения жидкости методом Эйлера геометрической характеристикой движения служит линия тока. Линия тока −это линия, касательные к которой в любой точке совпадают с направлением вектора скорости частицы жидкости в данной точке. Для её построения выберем в пространстве, занятом движущейся жидкостью, некоторую точку A1 (рис.1а) и проведем в этой точке отвечающий ей в данный момент времени вектор скорости 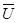 1. Затем возьмем точку А2, лежащую на векторе
1. Затем возьмем точку А2, лежащую на векторе 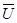 2 вблизи точки A1, и проведем вектор скорости
2 вблизи точки A1, и проведем вектор скорости 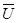 2, относящийся к тому же самому моменту времени, и т.д. Получим ломаную линию А1А2А3….., которая в пределе (при большом количестве точек, бесконечно близких друг к другу) обратится в кривую, которая и будет линией тока. В случае нестационарного потока линии тока отражают мгновенную картину движения жидкости, отвечающую определенному моменту времени. Касательные к линии тока фиксируют направления скорости разных частиц (А1,А2,А3) в последовательных точках пространства в один и тот же момент времени t = t 1. Касательные к траектории дают направление скорости одной и той же частицы (А1) в последовательные моменты времени (t 1, t 2 , t 3). Траектория частицы А1 имеет лишь одну общую точку с линией тока, отвечающей моменту времени t = t 1 (рис.1б).
2, относящийся к тому же самому моменту времени, и т.д. Получим ломаную линию А1А2А3….., которая в пределе (при большом количестве точек, бесконечно близких друг к другу) обратится в кривую, которая и будет линией тока. В случае нестационарного потока линии тока отражают мгновенную картину движения жидкости, отвечающую определенному моменту времени. Касательные к линии тока фиксируют направления скорости разных частиц (А1,А2,А3) в последовательных точках пространства в один и тот же момент времени t = t 1. Касательные к траектории дают направление скорости одной и той же частицы (А1) в последовательные моменты времени (t 1, t 2 , t 3). Траектория частицы А1 имеет лишь одну общую точку с линией тока, отвечающей моменту времени t = t 1 (рис.1б).
При стационарном движении линии тока для различных моментов времени совпадают и вместе с тем имеют место их совпадения с траекториями. Это легко понять, если учесть, что каждая частица в любой точке, лежащей на её траектории, имеет то же направление ( и величину ) скорости, что и все остальные частицы, проходящие через эту точку. Действительно, пусть кривая на рис.1 представляет траекторию частицы А1. В точке I, через которую эта частица проходит в момент времени t 1 , вектор скорости будет UA 1 ( t 1 ). Но в силу стационарности потока такую же скорость (по величине и направлению) будет иметь и частица A 2, проходящая через точку I в другой момент времени t 2, когда частица А1, следуя вдоль своей траектории, окажется в точке 2. Таким образом, в один и тот же момент времени t 2 две частицы А1 и А2 оказываются на одной и той же траектории, следовательно, эта кривая является одновременно и линией тока.
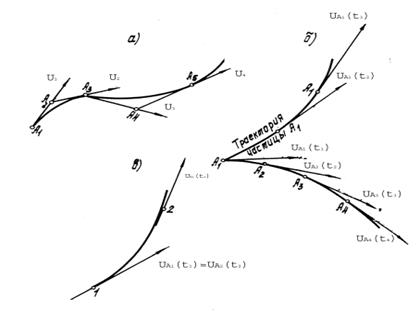
Рис.1
3.3. Уравнение линии тока
Уравнение линии тока легко составить, пользуясь такими рассуждениями. Допустим, что в данный момент времени имеем плоскую линию тока а (рис.2).
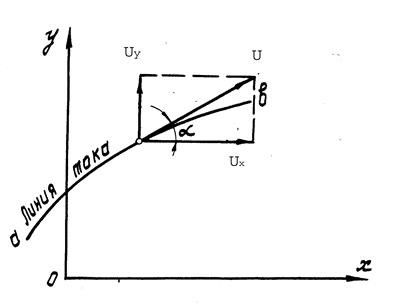
Рис.2
Очевидно, уравнение этой линии можно записать так:
y = f(x),
где x и y − координаты точек данной линии.
Непосредственно из рис.2 имеем UY / UX = tg 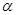 , а дифференцируя уравнение линии тока по x, находим
, а дифференцируя уравнение линии тока по x, находим
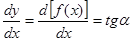 .
.
Таким образом, 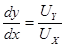 , или
, или
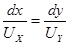 , или
, или 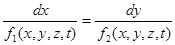 ,
,
что и является уравнением линии тока в дифференциальном виде.
При пространственном движении дифференциальные уравнения линии тока записываются так: 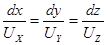 ,
,
или
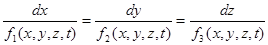 . (3.10)
. (3.10)
Проинтегрировав уравнения (3.10), можно получить уравнение линии тока в конечном виде. Решение этой системы может быть записано в виде двух общих интегралов:
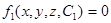 ;
;
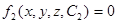 ,
,
где С1 и С2 −произвольные постоянные интегрирования.
Каждый из интегралов представляет в геометрическом отношении семейство поверхностей, зависящих от постоянных С1 и С2. Линия тока, отвечающая определенным значениям этих постоянных, находится как линия пересечения двух соответствующих поверхностей.
Если внутри движущейся жидкости выделить некоторый замкнутый контур L (рис.3) и через все его точки провести для данного момента времени линии тока, то они образуют поверхность, называемую поверхностью тока. На рис.3 представлена схема струйки в непрерывном потоке.
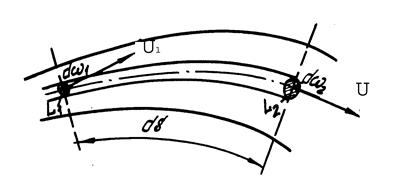
Рис.3
Часть жидкости, ограниченная этой поверхностью, получила название трубки тока.
В нестационарном потоке форма трубок тока непрерывно изменяется, поскольку изменяется направление линии тока. Важнейшим свойством трубки тока является непроницаемость её боковой поверхности для движущихся частиц жидкости, что легко понять, если учесть, что эта поверхность образована линиями тока.
Наряду с трубкой тока в гидродинамике пользуются еще понятием струйки. Струйкой называют часть жидкости, ограниченной поверхностью, образованной совокупностью траекторий, проходящих через все точки замкнутого контура. Для стационарного потока понятия трубки тока и элементарной струйки идентичны, так как линии тока и траекторий в этом случае совпадают.
Струйка имеет малую площадь поперечного сечения 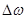 (в пределе
(в пределе 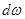 ), которая может меняться по длине.
), которая может меняться по длине.
Совокупность элементарных струек образует поток жидкости.
3.4. Понятия расхода, средней скорости, живого сечения,
Глава четвертая
Невязкой жидкости
В потоке жидкости рассмотрим движение элементарного объема в форме параллелепипеда со сторонами dx , dy , dz (рис. 1).
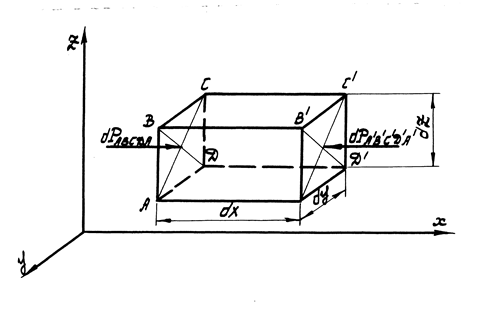
Рис. 1
Напишем второй закон Ньютона для массы жидкости в этом объеме сначала в проекциях на ось Ox:
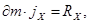 (4.1)
(4.1)
где масса 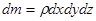 , а проекция ускорения
, а проекция ускорения
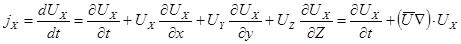 .
.
Определим проекцию на ось Ox равнодействующих внешних сил. Проекция силы давления на боковую грань АВСД
dP АВСДА = p · dy · dZ ,
где p − среднее давление в пределах указанной грани.
Среднее давление в пределах грани 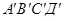
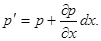
Следовательно, сила давления на эту грань
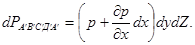
С учетом того что проекция на ось OX силы давления на другие грани параллелепипеда равна нулю, сумма проекций сил давления на боковые грани АВСД и  будет равна
будет равна
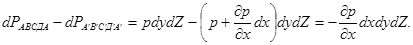
Проекция объемных сил на ось Ox можно представить в виде
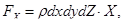
где X –проекция ускорения на ось OX .
Подставляя выражение для проекций сил в формулу (1), получим
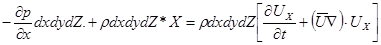
или после сокращения на 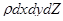 , т.е. отнеся все члены уравнения к единице массы жидкости в рассматриваемом объеме,
, т.е. отнеся все члены уравнения к единице массы жидкости в рассматриваемом объеме,
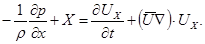
Аналогичные уравнения можно написать и для других координатных осей. В результате получим следующую систему уравнений
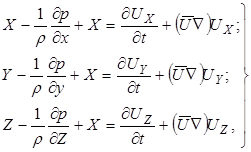 (4.2)
(4.2)
которая называется системой уравнений Л.Эйлера для движения сплошной среды.
В систему из трех уравнений входят четыре неизвестные функции:U X , U Y , U Z и p. Поэтому для ее решения необходимо иметь еще одно уравнение, которое связало бы между собой названные функции. Таким уравнением является рассмотренное выше уравнение неразрывности (3.15).
4.2. Дифференциальные уравнения движения
вязкой жидкости (уравнения Навье-Стокса)
Дифференциальные уравнения движения вязкой жидкости могут быть составлены путем дополнения уравнений Л.Эйлера слагаемыми, учитывающими вязкость жидкости. Тогда уравнения Эйлера запишутся в виде
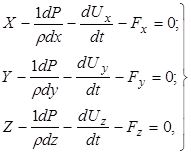 (4.3)
(4.3)
где Fx ,Fy, и Fz −проекции сил вязкости, отнесенные к единице массы жидкости, на координатные оси. Найдем силы Fx ,Fy и Fz , предполагая, что жидкость движется слоями, т.е. без перемешивания. Под действием сил вязкости возникают как тангенциальные, так и нормальные напряжения.
Выделим элемент движущейся жидкости в форме параллелепипеда с ребрами, параллельными координатным осям, и определим сумму проекций сил вязкости, действующих только на те три грани параллелепипеда, которые образуют трехгранный угол с вершиной А (рис. 2).

Рис.2
Для удобства дальнейших рассуждений введем двойную индексацию напряжения, например: для нормального напряжения − рхх, касательного напряжения − 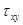 и т.д. Здесь первый индекс указывает на то, что площадка, для которой определяется напряжение, расположена нормально к данной оси координат, а второй –направление действия напряжения. С учетом этого получим выражение для проекций сил, действующих на грани трехгранного угла с вершиной А:
и т.д. Здесь первый индекс указывает на то, что площадка, для которой определяется напряжение, расположена нормально к данной оси координат, а второй –направление действия напряжения. С учетом этого получим выражение для проекций сил, действующих на грани трехгранного угла с вершиной А:
ось ОХ 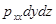 ;
; 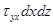 ;
; 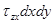 ;
;
ось О Y 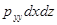 ;
; 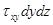 ;
; 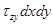 ;
;
ось О Z 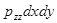 ;
; 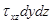 ;
; 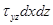 .
.
Переходя затем к проекциям сил, действующих на грани трехгранного угла с вершиной С, отметим, что напряжения на этих гранях будут отличаться от напряжений на гранях трехгранного угла с вершиной А.
Итак, выражения для проекций сил, действующих на грани трехгранного угла с вершиной С:
ось ОХ 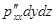 ;
; 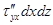 ;
; 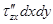 ;
;
ось О Y 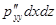 ;
; 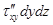 ;
; 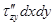 ;
;
ось О Z 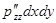 ;
; 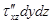 ;
; 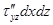 ;
;
где для оси OX
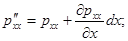

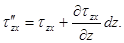
Аналогичные уравнения можно получить и для двух других осей координат.
Составим теперь уравнение для силы, представляющей собой сумму проекций на ось OX сил вязкости.
Полагая, что направление сил, действующих на грани угла с вершиной 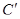 , противоположно направлению сил, действующих на грани трехгранного угла с вершиной А, получим
, противоположно направлению сил, действующих на грани трехгранного угла с вершиной А, получим
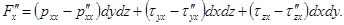
Но
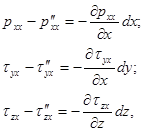
в силу чего, делая соответствующую подстановку, найдем

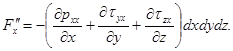
Сила Fx, входящая в уравнение Эйлера, как указано выше, представляет собой проекцию силы вязкости, отнесенной к единице массы жидкости, т.е. 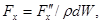 где в данном случае
где в данном случае 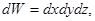 а поэтому для силы Fx получим выражение
а поэтому для силы Fx получим выражение
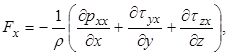 (4.4)
(4.4)
где рхх −нормальные, 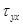 и
и 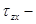 касательные напряжения.
касательные напряжения.
Касательные напряжения 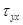 в пределах грани dxdy остаются одинаковыми для всех ее точек, т.е. не зависят от координат X и Y и изменяются только при перемешивании этой грани вдоль оси OY, т.е. зависят от координаты Y .
в пределах грани dxdy остаются одинаковыми для всех ее точек, т.е. не зависят от координат X и Y и изменяются только при перемешивании этой грани вдоль оси OY, т.е. зависят от координаты Y .
Другими словами, 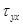 −это касательные напряжения, зависящие только от градиента скорости
−это касательные напряжения, зависящие только от градиента скорости 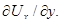 Поэтому в соответствии с законом внутреннего трения в жидкости Ньютона
Поэтому в соответствии с законом внутреннего трения в жидкости Ньютона 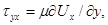 а
а 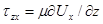 (по аналогии).
(по аналогии).
Рассмотрим производную 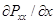 . Здесь Pxx представляет собой нормальное к площадке dydz напряжение, обусловленное влиянием вязкости (сжатие в условиях торможения и растяжение при ускоренном движении). Поэтому можно допустить, что напряжение Pxx может также определяться по закону Ньютона
. Здесь Pxx представляет собой нормальное к площадке dydz напряжение, обусловленное влиянием вязкости (сжатие в условиях торможения и растяжение при ускоренном движении). Поэтому можно допустить, что напряжение Pxx может также определяться по закону Ньютона 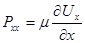 , тогда
, тогда
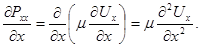
Делая соответствующие подставки в уравнение (4.4), получим
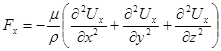 ,
,
или, так как 
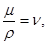

Аналогично для других координатных осей можно записать
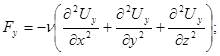
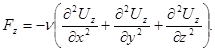
Вводя теперь полученные выражения для сил Fx , Fy , Fz в систему уравнений (4.3), после некоторой перестановки слагаемых получим дифференциальные уравнения движения вязкой жидкости:
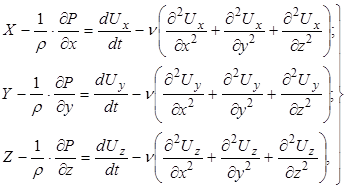 (4.5)
(4.5)
или окончательно
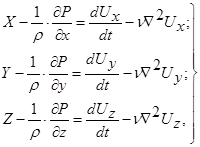 (4.6)
(4.6)
где 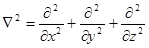 −оператор Лапласа.
−оператор Лапласа.
Эти уравнения именуются уравнениями Навье-Стокса. Они составляют основу гидродинамики реальной жидкости.
При решении конкретных задач о движении несжимаемой жидкости к уравнениям Навье-Стокса необходимо добавить уравнение неразрывности в форме
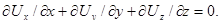
Таким образом, мы получаем замкнутую систему четырех уравнений, достаточную для определения четырех неизвестных величин: трех компонентов скорости Ux , Uy , Uz и давления P.
Кроме того, для определения произвольных постоянных и произвольных функций, появляющихся при интегрировании, должны быть сформулированы так называемые краевые условия, т.е. начальные и граничные условия.
Начальные условия, о которых может идти речь лишь в случае не стационарного движения, указываются посредством задания поля скоростей и давлений в какой-нибудь определенный (начальный) момент времени t = tx.
Задание граничных условий для случая движения вязкости жидкости сводится к признанию того факта, что частицы жидкости, непосредственно соприкасающиеся с поверхностью твердого тела, прилипают к ней и поэтому имеют одинаковую с ней скорость.
В частном случае при обтекании неподвижного тела граничное условие для скорости вязкой жидкости должно быть записано в виде V = 0.
Дифференциальные уравнения движения реальной жидкости представляют собой нелинейные уравнения второй степени в частных производных. В самом общем виде эти уравнения не могут быть проинтегрированы. Их решение возможно лишь для частных случаев, допускающих упрощение этих уравнений путем отбрасывания тех или иных членов. Уравнения движения критериев гидродинамического подобия будут рассмотрены ниже.
4.3. Критерии подобий и моделирование
Гидродинамических процессов
В связи с тем что в большинстве случаев практика решений уравнений Навье-Стокса встречает затруднения, в гидродинамике считают целесообразным прибегать к экспериментированию на моделях. При этом требуется соблюдение одновременного геометрического, кинематического и динамического подобия модели и натурного объекта.
Условимся все величины, относящиеся к модели, обозначать индексом М, а к натуре –Н.
Геометрическое подобие предусматривает пропорциональность сходственных линейных размеров. Если l н –некоторый размер в натуре, а l м−сходственный размер на модели, то при соблюдении геометрического подобия 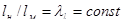 , где
, где 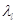 −геометрический масштаб моделирования. Имея в виду
−геометрический масштаб моделирования. Имея в виду 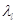 , отношение площадей и объемов можно выразить как
, отношение площадей и объемов можно выразить как
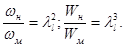
Кинетическое подобие заключается в соблюдении пропорциональности скоростей в сходственных точках натуры и модели в соответствующий момент времени 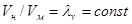 , где
, где 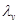 −кинематический масштаб моделирования. Для кинематически подобных систем соотношение
−кинематический масштаб моделирования. Для кинематически подобных систем соотношение 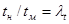 также является постоянной величиной. Здесь
также является постоянной величиной. Здесь 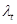 −масштаб времени, t н и t м –промежутки времени, в течение которых происходит процесс в натуре и на модели.
−масштаб времени, t н и t м –промежутки времени, в течение которых происходит процесс в натуре и на модели.
Динамическое подобие выражается пропорциональностью векторов сил, действующих в сходственных точках модели и натуры, т.е.
 где
где 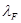 −масштаб сил. Для всех пар сходственных точек динамически подобных систем
−масштаб сил. Для всех пар сходственных точек динамически подобных систем 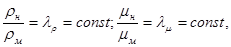
где 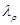 и
и 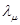 −соответственно масштабы плотности и вязкости.
−соответственно масштабы плотности и вязкости.
Динамически подобные системы могут быть названы механически подобными.
Для получения условий механического подобия применим метод, основанный на анализе дифференциального уравнения движения.
Запишем дифференциальное уравнение движения вязкой жидкости (уравнение Навье-Стокса) для двух сходственных точек натуры и модели:
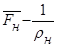
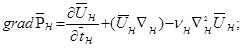 (4.7)
(4.7)
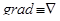 ;
; 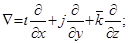
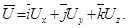
Отнесем все физические величины уравнения (4.7) к соответствующим масштабам и получим выражение
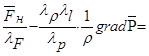
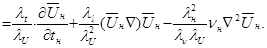 (4.8)
(4.8)
Разделив уравнение (4.8) на 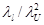 , получим
, получим
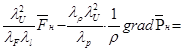

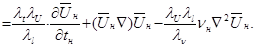 (4.9)
(4.9)
Заметим, что для механически подобных систем необходимо, чтобы
движение частиц жидкости в сходственных точках описывалось одинаковыми уравнениями.
Из сопоставления уравнений (4.7) и (4.9) видно, что они будут одинаковыми при равенстве безразмерных множителей в уравнении (4.9) единице, т.е.
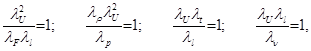
или
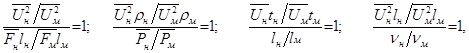
откуда

В общем случае между полученными критериями подобия существует функциональная связь:
 (4.10)
(4.10)
При установившемся движении жидкости локальная составляющая инерционной силы в дифференциальном уравнении Навье-Стокса отсутствует и, следовательно, число Струхаля из уравнения (4.9) выпадает, тогда функциональная связь принимает вид
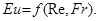 (4.11)
(4.11)
Условия моделирования, требующие одновременного соблюдения для натурного объекта и его модели одинаковости критериев Re и Fr не всегда могут быть выполнены:
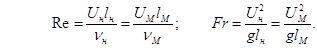
Предположим сначала, что в опытах на модели применяется та же жидкость, что и в натуральном обьекте, так что 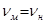 . Тогда, чтобы удовлетворить условию одинаковости критерия Re, соотношение между скоростями течений в модели и в натурном объекте должно быть равно
. Тогда, чтобы удовлетворить условию одинаковости критерия Re, соотношение между скоростями течений в модели и в натурном объекте должно быть равно
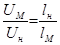 , (4.12)
, (4.12)
в то время как для соблюдения подобия по критерию Fr необходимо выполнение соотношения
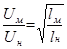 . (4.13)
. (4.13)
Несовместимость этих двух требований исключает возможность использования для модели жидкости с тем же значением кинематической вязкости, что и в натурном обьекте. Соотношение между 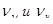 должно быть определено из критерия Re так, чтобы одновременно было соблюдено соотношение (4.13), вытекающее из критерия Fr.
должно быть определено из критерия Re так, чтобы одновременно было соблюдено соотношение (4.13), вытекающее из критерия Fr. 
Находим, что
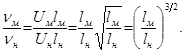
Естественно, что чем меньше будет масштаб модели, тем затруднительнее окажется подбор «модельной» жидкости. Даже при таком, например, сравнительно большом масштабе модели, как ¼ натуральной величины, «модельная» жидкость должна обладать вязкостью в восемь раз меньшей, чем в натурном объекте.
Подбор жидкости со столь отличной вязкостью далеко не всегда оказывается возможным.
В тех случаях, когда строгое моделирование оказывается невыполнимым, прибегают к приближенному моделированию. При этом во внимание принимается лишь один из названных критериев, тот, который для данной задачи имеет наиболее существенное значение.
При больших значениях критерия Рейнольдса, что отвечает значительному преобладанию инерционных сил над силами вязкости, можно в уравнении Навье-Стокса силами вязкости пренебречь. Тем самым критерий Рейнольдса окажется исключением из всех критериев. В таком случае для установившегося движения несжимаемой жидкости (при отсутствии влияния на движение массовых сил) критерий Эйлера Eu становится определяющим:
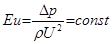 . (4.14)
. (4.14)
Область значения критерия подобия, в которой он практически перестает быть критерием, называется автомодельной относительно данного критерия.
4.4. Интегралы уравнения движения жидкости
Уравнения Эйлера для общего случая не интегрируются. Интегрирование возможно только в некоторых частных случаях при упрощающих предположениях. В зависимости от принятых допущений различают несколько случаев прямого интегрирования:
1. Интеграл Лагранжа-Коши для безвихревого неустановившегося движения.
2. Интеграл Л. Эйлера для безвихревого установившегося движения.
3. Интеграл Д. Бернулли для установившегося движения вдоль линии тока.
Все интегралы получены при условии, что массовые силы потенциальны.
4.5. Интеграл Лагранжа-Коши
Уравнения Бернулли
Рассмотрим геометрический смысл слагаемых, входящих в уравнение Бернулли.
Напишем уравнение Бернулли для элементарной струйки идеальной жидкости:
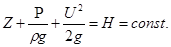
Все слагаемые уравнения имеют размерность длины.
Первый член уравнения Z определят высоту положения центра тяжести рассматриваемого сечения над горизонтальной плоскостью сравнения, его называют геометрической высотой, или геометрическим напором.
Второй член уравнения 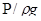 называется пьезометрической высотой, или пьезометрическим напором.
называется пьезометрической высотой, или пьезометрическим напором.
Третий член уравнения 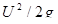 называется скоростной высотой, или скоростным напором.
называется скоростной высотой, или скоростным напором.
Так как все члены, входящие в уравнение Бернулли, имеют линейную размерность, следовательно, и их сумма, обозначенная через H, также имеет размерность длины. Величину H называют полным (гидродинамическим) напором в данном сечении струйки.
Слагаемые уравнения Бернулли можно изобразить графически, если отнести струйку к системе координат XYZ (рис. 3) и откладывать от горизонтальной плоскости XOY для ряда сечений геометрические напоры Z, пьезометрические − 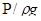 и скоростные −
и скоростные − 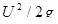 высоты. Соединив концы отрезков, выражающих скоростные напоры
высоты. Соединив концы отрезков, выражающих скоростные напоры 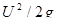 , получим горизонтальную линию H - H, расположенную на высоте H от координатной плоскости XOY. Линия H - H называется напорной, или линией полного напора.
, получим горизонтальную линию H - H, расположенную на высоте H от координатной плоскости XOY. Линия H - H называется напорной, или линией полного напора.
Соединив концы отрезков, выражающих пьезометрические высоты 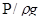 , получим линию Р-Р, которая называется пьезометрической. Эта линия изображает изменение суммы геометрической и пьезометрической высот вдоль струйки при движении идеальной жидкости.
, получим линию Р-Р, которая называется пьезометрической. Эта линия изображает изменение суммы геометрической и пьезометрической высот вдоль струйки при движении идеальной жидкости.
Итак, график уравнения дает наглядное представление об изменении всех составляющих полного напора вдоль элементарной струйки при движении идеальной жидкости.
Рассмотрим механический смысл уравнения Бернулли для элементарной струйки идеальной жидкости. Напишем уравнение Бернулли для двух произвольных сечений, например 1-1 и 2-2:
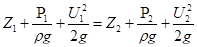 .
.
Перегруппировав все его члены, этому уравнению можно придать вид:
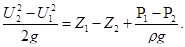 (4.28)
(4.28)
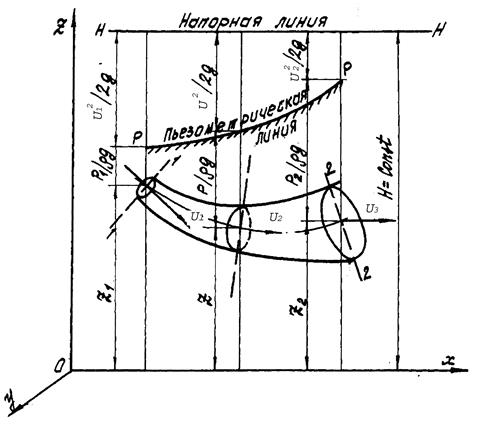
Рис. 3
Получили уравнение кинетической энергии для единицы веса жидкости. Слагаемые в правой части уравнения (4.28) выражают работы удельных сил тяжести и давления, имеют размерность работы. Левая часть уравнения представляет приращение кинетической энергии единицы веса жидкости и также имеет размерность работы. Таким образом, с механической точки зрения слагаемые, входящие в уравнение Бернулли, выражают работу единицы веса жидкости, так как удельные работы можно заменить эквивалентными величинами удельных энергий. Следовательно, можно заключить, что слагаемые, входящие в уравнение Бернулли, выражают удельные энергии струйки, т.е. Z – удельная энергия положения, 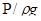 − удельная энергия давления,
− удельная энергия давления, 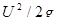 − удельная кинетическая энергия и
− удельная кинетическая энергия и 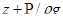 − удельная потенциальная энергия.
− удельная потенциальная энергия.
Из уравнения Бернулли для струйки идеальной жидкости следует, что полная удельная энергия 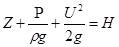 постоянна по длине струйки.
постоянна по длине струйки.
4.9. Уравнение Д. Бернулли
Для турбулентного движения
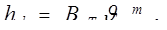
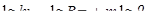 .
.
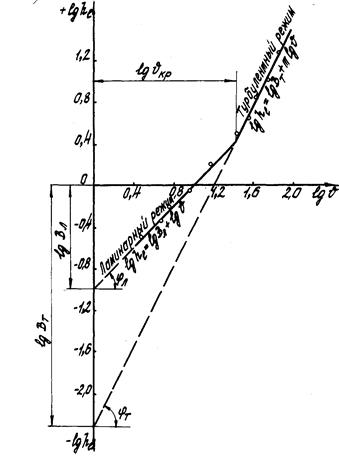
Рис.2
Здесь также получили прямую, но угловой коэффициент этой прямой другой и равен 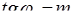 , в то время как в первом случае мы имели
, в то время как в первом случае мы имели 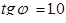 (см. рис. 2).
(см. рис. 2).
Различие кинематической структуры ламинарного и турбулентного потоков изменяет характер зависимости потери по длине 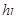 от средней скорости
от средней скорости 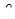 .
.
Турбулентные пульсации порождают дополнительные касательные напряжения, которые обуславливают увеличение потерь энергии в турбулентных потоках, по сравнению с ламинарными, при сопоставимых условиях.
5.4. Основное уравнение равномерного движения
В цилиндрической трубе
Равномерное движение возможно лишь в трубах постоянного сечения, так как при равномерном движении величина средней скорости и распределение скоростей по сечению должны оставаться неизменными по длине трубопровода.
Найдем выражение для равномерного движения жидкости в трубах, справедливое как для ламинарного, так и турбулентного режимов.
Пусть в наклонном трубопроводе имеем равномерное движение со средней скоростью 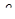 .
.
Сечениями 1-1 и 2-2 в трубопроводе выделим соосную цилиндрическую струйку радиусом 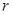 и длиной
и длиной  (рис. 3).
(рис. 3).
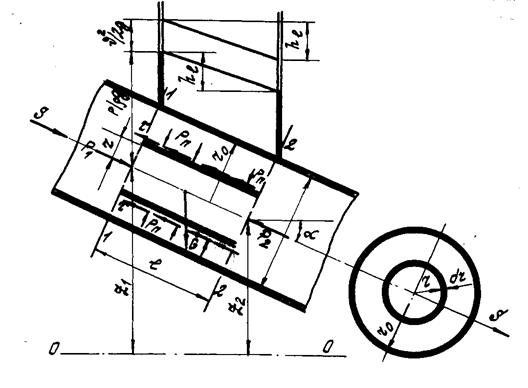
Рис.3
Для выделенного отсека уравнение динамического равновесия относительно оси движения S - S можно записать в виде
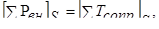
где 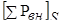 –сумма проекций внешних сил на ось движения;
–сумма проекций внешних сил на ось движения; 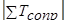 –сумма проекций сил сопротивления на ось движения.
–сумма проекций сил сопротивления на ось движения.
Внешние силы:
1. Сила тяжести 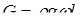 проекция которой на ось равна:
проекция которой на ось равна:
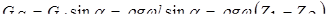 , (5.7)
, (5.7)
где 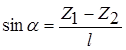
2. Силы давления на торцевые поверхности отсека: 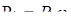 и
и 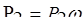 .
.
Сумма проекций этих сил на ось S - S будет
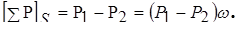 (5.8)
(5.8)
3. Силы давления на боковую поверхность направлены перпендикулярно к оси движения S - S, поэтому проекции этих сил будут равны нулю.
4. Суммарная сила сопротивления (трения) спроектируется на ось движения в натуральную величину и может быть выражена зависимостью
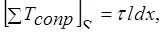 (5.9)
(5.9)
где 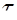 –сила сопротивления трения, приходящаяся на единицу боковой поверхности выделенного жидкого цилиндра (среднее касательное напряжение). Таким образом, с учетом выражений (5.7)–(5.9) уравнение динамического равновесия (5.6) можно представить в виде
–сила сопротивления трения, приходящаяся на единицу боковой поверхности выделенного жидкого цилиндра (среднее касательное напряжение). Таким образом, с учетом выражений (5.7)–(5.9) уравнение динамического равновесия (5.6) можно представить в виде
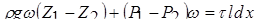 . (5.10)
. (5.10)
Разделив уравнение (10) на произведение 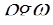 , получим
, получим
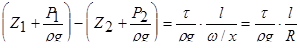 . (5.11)
. (5.11)
Поскольку левая часть уравнения (11) представляет собой в случае равномерного движения потерю напора по длине 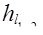 , можно это уравнение окончательно записать в виде
, можно это уравнение окончательно записать в виде
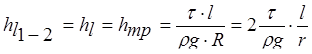 (5.12)
(5.12)
или
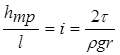 , (5.13)
, (5.13)
где 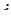 –гидравлический или пьезометрический уклоны, так как при равномерном движении эти уклоны равны.
–гидравлический или пьезометрический уклоны, так как при равномерном движении эти уклоны равны.
Уравнение (5.13) является основным уравнением равномерного движения жидкости в цилиндрической трубе.
5.5. Общее выражение потерь напора на трение
Рис.5
У стенок трубы ( 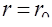 ) скорость равняется нулю, на оси трубы (
) скорость равняется нулю, на оси трубы (  0) скорость имеет максимальное значение, равное
0) скорость имеет максимальное значение, равное
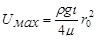 . (5.28)
. (5.28)
Рис. 7
Действительное значение скорости может быть представлено как сумма осредненной и пульсационной скоростей:
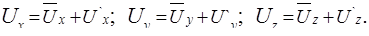 (5.34)
(5.34)
Период осреднения Т должен выбираться достаточно большим по сравнению с периодом пульсаций.
Из равенств (5.34) следует, что осредненные пульсационные скорости должны быть равны нулю. Действительно, подставив под знак интеграла в выражении (5.33) значение 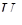 , получим
, получим
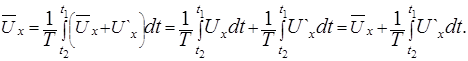 (5.35)
(5.35)
Из равенства (5.35) следует, что
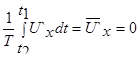 . (5.36)
. (5.36)
Если осредненные величины оказываются для разных последовательных моментов времени постоянными, то такое турбулентное движение считают установившимся.
Уравнение Рейнольдса
Подставив в уравнение Навье-Стокса вместо компонентов скорости их выражения через осредненные и пульсационные величины для установившегося турбулентного движения, получаем уравнения Рейнольдса:
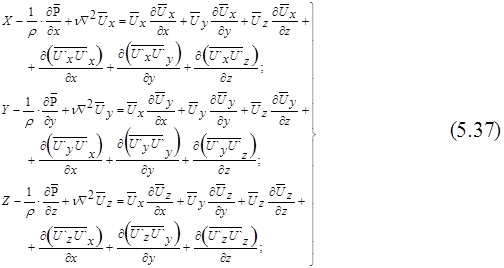
По сравнению с уравнением Навье-Стокса каждое из уравнений движения системы (5.37) включает еще три дополнительных члена, зависящих от пульсаций скорости. Представив каждый из этих членов, например в форме 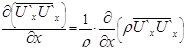 , перепишем уравнения Рейнольдса, перенося все члены, зависящие от пульсаций, в левую часть. Для краткости напишем только первое уравнение
, перепишем уравнения Рейнольдса, перенося все члены, зависящие от пульсаций, в левую часть. Для краткости напишем только первое уравнение
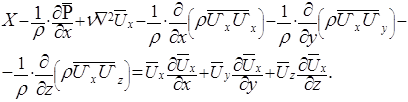
Теперь мы видим, что наряду с членами вида
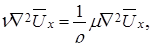
выражающими действие вязкостных напряжений, уравнения Рейнольдса содержат члены вида, которые выражают действие напряжений, присущих только турбулентному потоку:
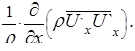
Таким образом, в турбулентном потоке полные касательные напряжения слагаются из вязкостных и турбулентных:
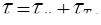 (5.38)
(5.38)
причем турбулентные напряжения выражаются формулой и обладают свойством взаимности 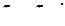
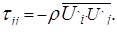
5.9. Гипотезы Буссинеска и Прандтля
О турбулентных напряжениях
Рассмотрим прямолинейный установившийся турбулентный поток с неравномерным распределением усредненных скоростей (рис. 8).
Одна из существующих гипотез о связи турбулентного напряжения 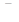 с усредненной скоростью
с усредненной скоростью 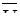 заключается в том, что эта связь может быть выражена формулой
заключается в том, что эта связь может быть выражена формулой
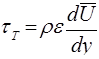 . (5.39)
. (5.39)
Эта формула предложена Буссинеском.
Коэффициент 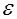 , получивший название кинематического коэффициента турбулентной вязкости, имеет размерность
, получивший название кинематического коэффициента турбулентной вязкости, имеет размерность 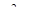 . Наиболее простую физическую модель турбулентного потока, позволяющую установить некоторые общие закономерности движения, дает гипотеза Прандтля. Согласно этой гипотезе
. Наиболее простую физическую модель турбулентного потока, позволяющую установить некоторые общие закономерности движения, дает гипотеза Прандтля. Согласно этой гипотезе
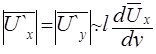 (5.40)
(5.40)
и, следовательно,
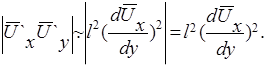
Модуль касательного турбулентного напряжения теперь выражается в виде
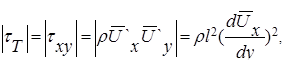 (40)
(40)
где коэффициент 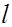 , имеющий размерность длины, получил название длины пути перемешивания.
, имеющий размерность длины, получил название длины пути перемешивания.
Чтобы пояснить это понятие, допустим, что жидкая частица, имевшая в слое 1 усредненную скорость 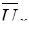 (см. рис. 8), под влиянием турбулентной пульсации
(см. рис. 8), под влиянием турбулентной пульсации 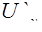 перемещается на расстояние
перемещается на расстояние 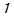 , в слой 2, где усредненная скорость равна
, в слой 2, где усредненная скорость равна 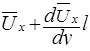 . Основное допущение данной теории заключается в том, что путь между слоями 1 и 2 жидкая частица проходит без взаимодействия с другими частицами, т.е. так, как молекула газа проходит путь свободного пробега. Тогда в результате смешения с частицами слоя 2 переместившаяся частица приобретает усредненную скорость этого слоя, т.е. в нем будет иметь место пульсация продольной скорости.
. Основное допущение данной теории заключается в том, что путь между слоями 1 и 2 жидкая частица проходит без взаимодействия с другими частицами, т.е. так, как молекула газа проходит путь свободного пробега. Тогда в результате смешения с частицами слоя 2 переместившаяся частица приобретает усредненную скорость этого слоя, т.е. в нем будет иметь место пульсация продольной скорости.

Рис. 8
На рис.8 представлен турбулентный установившийся поток вблизи плоскости стенки.
Используя (5.39) и (5.41), легко установить связь между кинематическим коэффициентом турбулентной вязкости 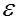 и длиной пути перемешивания
и длиной пути перемешивания 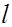 :
:
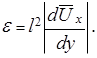 (5.42)
(5.42)
Гипотеза Буссинеска, как и гипотеза Прандтля, сводит задачу отыскания связи турбулентных касательных напряжений с полем усредненных скоростей к другой задаче – определению некоторой функции координат 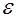 или
или 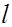 , характерной для турбулентного потока.
, характерной для турбулентного потока.
Решения этой второй задачи основаны или только на экспериментальных данных, или на дополнительных гипотезах. Так, например, Л. Прандтль предположил, что для полубезграничного турбулентного потока вблизи плоской стенки справедлива линейная связь пути перемешивания 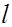 и расстояния от стенки
и расстояния от стенки 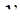 : l = ϰy, где ϰ –универсальная постоянная.
: l = ϰy, где ϰ –универсальная постоянная.
5.10. Турбулентное движение жидкости
Рис.11
На рис. 10 представлена схема движения потока жидкости при резком изменении поперечного сечения трубопровода: а)резком расширении потока; б)сужении потока.
Результаты экспериментальных исследований разных авторов показывают, что при больших числах Re имеет место область квадратичного сопротивления, где значение коэффициента 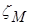 зависит только от конфигурации граничных поверхностей и не зависит от рода жидкости и скорости течения.
зависит только от конфигурации граничных поверхностей и не зависит от рода жидкости и скорости течения.
При малых же числах Re значение коэффициента 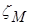 зависит не только от Re, но и от размеров потока и геометрических форм, граничных поверхностей.
зависит не только от Re, но и от размеров потока и геометрических форм, граничных поверхностей.
Численные значения коэффициентов 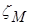 для различных местных сопротивлений, наиболее часто встречающихся в инженерной практике, приводятся в гидравлических справочниках.
для различных местных сопротивлений, наиболее часто встречающихся в инженерной практике, приводятся в гидравлических справочниках.
Рассмотрим подробнее местное сопротивление в виде внезапного расширения трубы (см. рис. 11). Наблюдения показывают, что при выходе струи из узкой части трубы образуется отрыв потока от стенок и пространство между струей и стенками заполняется вихрями. На некотором расстоянии 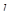 струя полностью расширяется, но может иметь в сечении
струя полностью расширяется, но может иметь в сечении 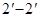 резко неравномерную эпюру скоростей, что обусловлено нарушением оссемметричности (искривлением) потока на участке
резко неравномерную эпюру скоростей, что обусловлено нарушением оссемметричности (искривлением) потока на участке 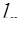 . Выравнивание эпюры скоростей происходит на участке
. Выравнивание эпюры скоростей происходит на участке 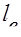 , в конце которого (сечение 2–2) устанавливается распределение скоростей, характерное для стабилизированного турбулентного потока. Поскольку перестройка эпюры скоростей сопровождается дополнительными потерями (помимо потерь на трение), то в расчетный участок местного сопротивления
, в конце которого (сечение 2–2) устанавливается распределение скоростей, характерное для стабилизированного турбулентного потока. Поскольку перестройка эпюры скоростей сопровождается дополнительными потерями (помимо потерь на трение), то в расчетный участок местного сопротивления 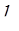 включает
включает 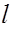 , полагая
, полагая 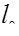 =
= 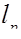 +
+ 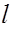 . Выбрав расчетные сечения 1–1 и 2–2, как показано на рис.11а, выразим потери на внезапное расширение по уравнению Бернулли
. Выбрав расчетные сечения 1–1 и 2–2, как показано на рис.11а, выразим потери на внезапное расширение по уравнению Бернулли
 (5.63)
(5.63)
В дальнейшем (для простоты) будем полагать, что  =
= 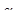 =1.
=1.
Чтобы исключить разность давлений, применим к отсеку жидкости, ограниченному сечениями 1–1 и 2–2 и боковой поверхностью трубы (контрольная поверхность на рис.2 показана штриховой линией), уравнение количества движения
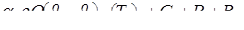 (5.64)
(5.64)
где 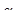 –корректив количества движения, который для сечений 1–1 и 2–2 можно принять равным единице;
–корректив количества движения, который для сечений 1–1 и 2–2 можно принять равным единице; 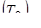 –проекция на направление движения внешней силы трения
–проекция на направление движения внешней силы трения 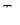 , действующей со стороны стенок трубы на рассматриваемый отсек жидкости. Так как длина участка потока между сечениями 1–1 и 2–2 невелика, то силой
, действующей со стороны стенок трубы на рассматриваемый отсек жидкости. Так как длина участка потока между сечениями 1–1 и 2–2 невелика, то силой 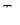 пренебрегаем и считаем
пренебрегаем и считаем 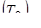 =0 (1-е допущение).
=0 (1-е допущение). 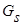 –проекция собственного веса отсека на направление движения,
–проекция собственного веса отсека на направление движения, 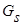 =0;
=0; 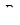 –сумма проекций на ось S сил гидродинамического давления
–сумма проекций на ось S сил гидродинамического давления  и
и 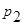 , действующих соответственно на торцевые сечения 1–1 и 2–2 выделенного отсека транзитной струи; R – проекция реакции стенок; величина
, действующих соответственно на торцевые сечения 1–1 и 2–2 выделенного отсека транзитной струи; R – проекция реакции стенок; величина 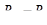 , где R –давление вертикальной стенки, имеющей кольцевую форму.
, где R –давление вертикальной стенки, имеющей кольцевую форму.
Величину 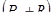 можно представить в виде
можно представить в виде
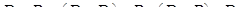 (5.65)
(5.65)
Измерения показывают, что в сечении 2–2 давление распределяется по гидростатическому закону, а в пределах кольцевой площади мало отличается от давления 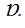 . При этом можем написать:
. При этом можем написать:
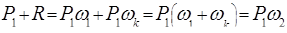 ;
;
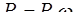 .
.
Упростив уравнение (5.65) и учтя уравнение неразрывности  , находим
, находим
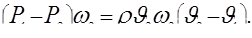
Следовательно,
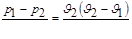 .
.
Теперь уравнение Бернулли (5.63) можно записать в виде
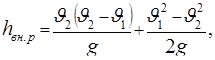
или, после упрощений
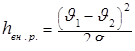 .
.
Эта формула, называемая формулой Борда, показывает, что потеря напора при внезапном расширении потока равна скоростному напору, вычисленному по потерянной скорости ( 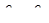 ). Учитывая уравнение неразрывности, формулу Борда нетрудно привести к виду, аналогичному формуле Вейсбаха (5.17), и получить теоретическое выражение для коэффициента сопротивления
). Учитывая уравнение неразрывности, формулу Борда нетрудно привести к виду, аналогичному формуле Вейсбаха (5.17), и получить теоретическое выражение для коэффициента сопротивления 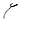 .
.
Действительно, поскольку 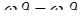 , то
, то
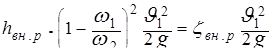 ,
,
и, следовательно,
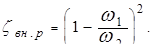 (5.66)
(5.66)
В частном случае, когда 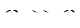 , т.е. имеет место сопряжение трубы с большим резервуаром, будет
, т.е. имеет место сопряжение трубы с большим резервуаром, будет 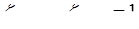 или
или 
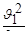 .При пользовании формулой (5.66) необходимо иметь в виду допущения, исходя из которых она выведена. Одним из них является предположение о близости к единице коэффициентов
.При пользовании формулой (5.66) необходимо иметь в виду допущения, исходя из которых она выведена. Одним из них является предположение о близости к единице коэффициентов 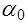 и
и 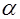 . Поэтому при значительной неравномерности распределения скоростей перед расширением (когда эти коэффициенты существенно отличны от единицы) формула (5.66) требует уточнения. Такое уточнение можно получить, если при выходе не делать допущения о том, что
. Поэтому при значительной неравномерности распределения скоростей перед расширением (когда эти коэффициенты существенно отличны от единицы) формула (5.66) требует уточнения. Такое уточнение можно получить, если при выходе не делать допущения о том, что 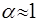 . Другое ограничение формулы Борда связано с влиянием на числа Рейнольдса. Оно проявляется при
. Другое ограничение формулы Борда связано с влиянием на числа Рейнольдса. Оно проявляется при 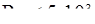 , а при малых числах Re становится преобладающим, поэтому формула (5.66) может давать удовлетворительные результаты лишь при квадратичной области сопротивления.
, а при малых числах Re становится преобладающим, поэтому формула (5.66) может давать удовлетворительные результаты лишь при квадратичной области сопротивления.
Заметим, наконец, что согласно выводу формулой Борда учитываются только потери на расширение, т.е. то превышение местных потерь над потерями по длине на участке, равном расчетному участку 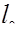 , которое вызвано увеличением диссипации энергии в местном сопротивлении. Если расчетный участок
, которое вызвано увеличением диссипации энергии в местном сопротивлении. Если расчетный участок 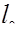 =
= 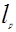 +
+ 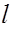 велик, то потери на трение здесь могут быть сопоставимы с потерями на расширение, и пренебрегать ими нельзя. Поэтому при постановке опыта для определения потерь на расширение следует из потерь, измеренных в опыте, вычесть потери по длине на участке эквивалентной длины.
велик, то потери на трение здесь могут быть сопоставимы с потерями на расширение, и пренебрегать ими нельзя. Поэтому при постановке опыта для определения потерь на расширение следует из потерь, измеренных в опыте, вычесть потери по длине на участке эквивалентной длины.
Это замечание относится и к другим видам местных сопротивлений.
5.13. Определение длины влияния местных сопротивлений
В качестве основной характеристики взаимного влияния местных сопротивлений принимается длина влияния, под которой понимают длину прямого участка трубопровода после местного сопротивления, в пределах которого прекращается возмущающее влияние сопротивления на поток. Установлено, что в общем случае величина длины влияния зависит от вида (геометрии) местного сопротивления, числа Рейнольдса, диаметра и относительной шероховатости трубопровода.
По А.Д. Альтштулю длина влияния для всей области турбулентного режима может быть определена по формуле
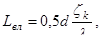 (5.67)
(5.67)
где 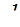 –диаметр трубопровода в квадратичной области;
–диаметр трубопровода в квадратичной области; 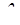 –коэффициент гидравлического сопротивления трубопровода.
–коэффициент гидравлического сопротивления трубопровода.
При больших числах Рейнольдса для ориентировочной оценки длины влияния приближенно можно принимать
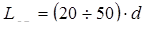 . (5.68)
. (5.68)
Глава шестая
СВОБОДНЫЕ СТРУИ
6.1. Истечение жидкости через малые отверстия
Рис.6
Последнюю зависимость можно прочитать так: для сходственных точек всех поперечных сечений отношение 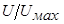 есть величина постоянная:
есть величина постоянная:
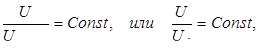
где 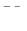 –скорость в произвольной точке сечения струи.
–скорость в произвольной точке сечения струи.
Однако это подобие эпюр скоростей не следует понимать как простое геометрическое подобие между ними. Это подобие представляет собой некоторое однообразие в форме эпюры. Оно заключается, по существу, в одной и той же закономерности распределения скоростей во всех сечениях основного участка струи. В связи с этим, если известны эпюра скоростей и закономерность изменения скорости в какой-либо характерной точке сечения, например в осевой точке  , то этим полностью определяется все поле скоростей струи.
, то этим полностью определяется все поле скоростей струи.
Г.Н. Абрамович дает следующее уравнение осевой скорости для круглой струи:
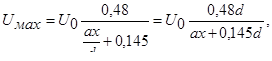 (6.19)
(6.19)
где x –расстояние от «полюса» до рассматриваемого сечения струи; d –диаметр выходного отверстия; a –коэффициент турбулентности или коэффициент структуры, учитывающий структуру потока в выходном сечении.
Для практических расчетов можно принимать a=0,08.
Все параметры круглой струи определяются по формулам
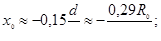 (6.20)
(6.20)
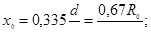 (6.21)
(6.21)
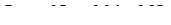 ; (6.22)
; (6.22)
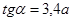 . (6.23)
. (6.23)
6.5. Незатопленная турбулентная струя
В этой струе можно выделить три характерные части: компактную, раздробленную и распыленную (рис.7).
В пределах компактной части струя сохраняет цилиндрическую форму, а сплошность потока еще не нарушается. В пределах раздробленной части сплошность струи нарушается, причем наблюдается ее постепенное расширение. Наконец, в пределах распыленной части струи происходит распад потока на отдельные капли. Разрушение струи, т.е. ее раздробление, а затем и распыление, объясняется аэрацией струи. Аэрация же, в свою очередь, обусловливается действием сил собственного веса жидкости и сил сопротивления воздуха, вызывающих турбулентный обмен частиц через границу между воздушной и водяной средами.
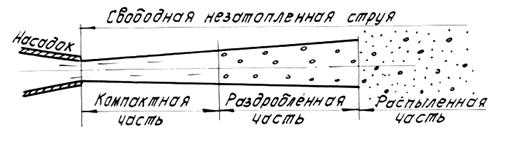
Рис.7
Уравнение теоретической траектории свободной струи выводится из предположения, что все частицы движутся совершенно одинаково, причем каждая, как свободная материальная точка в пустоте. В этом случае уравнение траектории (рис.8) в параметрической форме может быть представлено в виде:
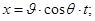 (6.24)
(6.24)
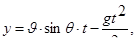 (6.25)
(6.25)
где 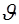 –начальная скорость;
–начальная скорость; 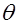 –угол наклона вектора начальной скорости к горизонту;
–угол наклона вектора начальной скорости к горизонту; 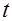 –время.
–время.
Исключая время, получим
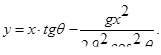 (6.26)
(6.26)
Полагая в последней формуле y =0, определим  –теоретическую дальность полета струи (дальность боя), откуда следует, что теоретическая максимальная дальность боя будет при
–теоретическую дальность полета струи (дальность боя), откуда следует, что теоретическая максимальная дальность боя будет при 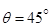
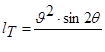 , (6.27)
, (6.27)
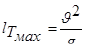 . (6.28)
. (6.28)
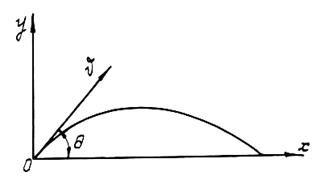
Рис.8
Формула (6.28) дает хорошее совпадение с опытом лишь при напорах истечения 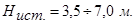
На дальность боя и высоту подъема струи оказывают влияние сопротивление воздуха и ветер. При этом на дальность боя ветер влияет больше, чем на высоту подъема.
Свободная незатопленная вертикальная струя, покидающая насадок со скоростью 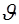 , направленной вертикально вверх, теоретически поднимается, как это следует из формулы (6.25), на высоту
, направленной вертикально вверх, теоретически поднимается, как это следует из формулы (6.25), на высоту 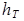 :
:
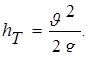
Глава седьмая
Разделив переменные

и проинтегрировав это уравнение в пределах для 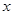 от
от 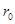 до
до 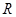 (где
(где 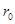 –радиус колодца) и соответственно для
–радиус колодца) и соответственно для 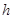 от
от 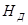 до
до 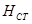 , т. е. пренебрегая участком высачивания
, т. е. пренебрегая участком высачивания
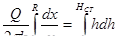 ,
,
получим следующее выражение:
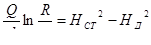 , (9.15)
, (9.15)
известное под названием формулы Дюпюи.
Расход, т.е. искомый дебит колодца, определяется выражением
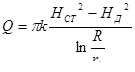 . (9.16)
. (9.16)
Для определения формы кривой депрессии необходимо, задаваясь различными значениями х (вместо R ), определить из уравнения (9.15) соответствующие им значения h ( вместо  ) и по точкам построить кривую, которая представляет собой параболу в координатах
) и по точкам построить кривую, которая представляет собой параболу в координатах  ,
, 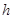 .
.
Опытными проверками установлено, что расход, определяемый по формуле Дюпюи, совпадает с действительным расходом, не смотря на неучет промежутка высачивания; положение же кривой депрессии при этом, естественно, определяется лишь приближенно.
9.5. Напорное движение грунтовых вод
Рассмотрим случай, когда водоносный пласт располагается между двумя водонепроницаемыми слоями и находится под избы точным давлением.
Если в таком пласте заложить колодец (скважину) и из него откачать воду, то толщина водоносного слоя, в отличие от случая, рассмотренного в предыдущем параграфе, не изменится, а изменится давление в пласте, убывая по направлению к колодцу. Отметим, что в тех случаях, когда глубина колодца меньше напора, соответствующего давлению в пласте до начала откачки, колодец будет фонтанировать и вода самоизливаться на поверхность земли.
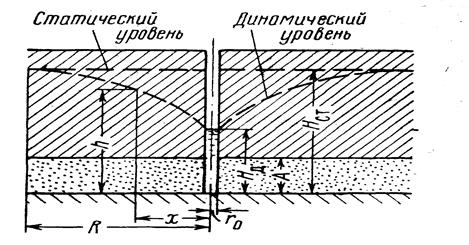
Рис.7
Подобного рода колодцы (скважины) обычно называют артезианскими. Пусть (рис.7). Толщина водоносного слоя будет А, напор в пласте на расстоянии R (радиус влияния) от оси колодца 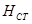 и высота уровня в колодце после откачки
и высота уровня в колодце после откачки 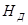 . Тогда, по аналогии с предыдущим, расход воды, проходящей через цилиндрическое сечение водоносного пласта, взятое на расстоянии х от оси колодца, будет
. Тогда, по аналогии с предыдущим, расход воды, проходящей через цилиндрическое сечение водоносного пласта, взятое на расстоянии х от оси колодца, будет
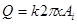 ,
,
где i –по-прежнему гидравлический уклон. Подставляя сюда вместо i его значение, равное  , разделяя переменные и интегрируя выражение
, разделяя переменные и интегрируя выражение
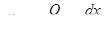
в пределах для х от 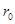 до
до 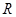 и для h от
и для h от 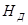 до
до 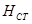 , получаем
, получаем
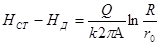 .
.
При этом дебит артезианского колодца при напорной фильтрации определяется выражением
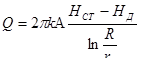 . (9.17)
. (9.17)
Так как последнее уравнение дает прямую линейную зависимость дебита от понижения уровня воды в колодце, для характеристики напорного водоносного пласта иногда вводят также понятие о так называемом удельном дебите, понимая под последним величину дебита при понижении уровня воды в колодце на 1 м.
Удельный дебит обычно определяется опытным путем на основании пробных откачек:
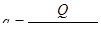 . (9.18)
. (9.18)
Применяемые в гидравлике
Так как гидравлика изучает законы равновесия и движения жидкостей, логично прежде всего рассмотреть некоторые физические свойства реальных жидкостей. Прежде чем перейти к изучению основных свойств жидкостей, остановимся на единицах измерения, принятых в гидравлике.
За основу принята Международная система единиц измерения (СИ). Кроме того, применяются внесистемные единицы. В инженерной практике используются такие системы МКГСС и СГС.
Основными единицами системы СИ являются:
единица длины – метр (м);
единица массы – килограмм (кг);
единица времени – секунда (с);
единица температуры – градус Кельвина ( К);
единицей силы является Ньютон (Н), т.е. сила, сообщающая массе в 1 кг ускорение в 1 м/с2.
Однако до сих пор в инженерной практике измеряют: давление (напор) в технических атмосферах (атм), метрах водяного столба и миллиметрах ртутного столба (м вод. ст. и мм рт. ст.), температуру в градусах Цельсия(0С), динамическую вязкость в пуазах(Пз) и кинематическую в стоксах (Ст), работу и энергию в киловаттчасах (кВт·ч).
Чтобы оценивать основные физические свойства жидкостей в различных системах единиц измерения, нужно знать соотношения между ними для этих свойств.
В системе СГС за единицу длины принят – см, за единицу времени – с, за единицу массы – г (масса 1 см3 воды при 40С).
Единицей силы в системе СГС служит длина, т.е. сила, которая массе в 1г сообщает ускорение, равное 1 см/с2.
Основные единицы в системе МКГСС:
единица длины – м, единица времени – с, единица силы – килограмм − сила (вес 1 дм3 дистиллированной воды при 40С).
За единицу массы здесь принимается масса, которая под действием силы в 1 кгс получает ускорение, равное 1м/с2. Эту единицу часто называют технической единицей массы (тем).
Назовем некоторые основные соотношения, которые служат для пересчета данных из одной системы единиц в другую
Если принять массу  m=1, ускорение a = 961 см/с2 (ускорение силы тяжести), то получим силу:
m=1, ускорение a = 961 см/с2 (ускорение силы тяжести), то получим силу:
в системе СГС (физической)
Рсгс = 1г · 981 см/с2 = 981 дина;
в системе СИ (международной)
РСИ = 0,001 кг · 9,81 м/с2 = 0,00981 Н;
в системе МКГСС (технической)
РМКГСС = 0,001 кгс.
Отсюда имеем
1Н = 100 000 дин = 0,102 кгс;
1 дина = 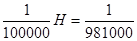 кгс;
кгс;
1 кгс = 9,81 Н = 981 000 дин.
Поступая подобным образом, можно найти также соотношение между единицами измерения массы в различных системах:
1 кг = 1000 г = 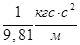 (тем).
(тем).
Размерности и единицы измерения других физических единиц, с которыми приходится иметь дело при гидравлических расчетах, легко получить как производные от установленных выше основных единиц измерения.
1.2. Основные физические свойства жидкостей
Плотность жидкостей
Плотностью жидкости 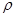 называется ее масса, заключенная в единице объема:
называется ее масса, заключенная в единице объема:
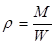 ,
, 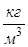 , (1.1)
, (1.1)
где М – масса жидкости; W – объем этой жидкости.
Плотность воды при 40С:
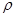 в 40С = 1000
в 40С = 1000 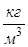 = 102
= 102 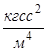 .
.
В практических приложениях о массе жидкости судят по ее весу.
Вес жидкости, приходящийся на единицу объема, называется удельным весом:
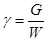 ,
,
где G – вес жидкости; W – объем этой жидкости.
Удельный вес воды при 40С
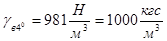 . (1.2)
. (1.2)
Поскольку
G = M · g , (1.3)
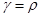 · g , (1.4)
· g , (1.4)
где g – ускорение свободного падения.
Относительным удельным весом жидкости (или относительным весом) 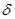 называется отношение удельного веса данной жидкости к удельному весу дистиллированной воды при 40С:
называется отношение удельного веса данной жидкости к удельному весу дистиллированной воды при 40С:
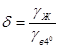 . (1.5)
. (1.5)
Сжимаемость капельных жидкостей под действием давления характеризуется коэффициентом объемного сжатия 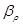 , который представляет собой относительное уменьшение объема жидкости на единицу увеличения напряжения сжатия:
, который представляет собой относительное уменьшение объема жидкости на единицу увеличения напряжения сжатия:
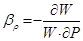 , (1.6)
, (1.6)
где W –первоначальный объем жидкости; 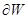 –уменьшение этого объема при увеличении сжимающего напряжения на величину
–уменьшение этого объема при увеличении сжимающего напряжения на величину 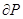 .
.
Коэффициент объемного сжатия в системе СИ имеет размерность 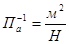 .
.
Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкости:
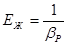 ,
, 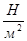 . (1.7)
. (1.7)
Как показывают исследования, при повышении сжимающего напряжения на 9,81 * 104 Па (1 ат) объем воды уменьшается в среднем на 1/20000 часть первоначальной величины.
Для воды
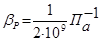 или
или 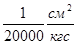 ,
,
ЕВ = 2 · 109 Па.
Вязкость жидкостей
Вязкостью называется свойство жидкостей оказывать сопротивление сдвигу. Все реальные жидкости обладают определенной вязкостью, которая проявляется в виде внутреннего трения при относительном перемещении смежных частиц или слоев жидкости. Таким образом, вязкость характеризует степень текучести жидкости или подвижности ее частиц.
Впервые наличие внутреннего трения в жидкостях было отмечено И. Ньютоном, высказавшем в 1687 г. гипотезу о том, что величина силы внутреннего трения между смежными слоями жидкости зависит от свойств жидкости, пропорциональна площади поверхности соприкасаемых слоев (площади трения) и их относительной скорости перемещения.
Справедливость гипотезы И. Ньютона была доказана русским ученым и инженером Н.П. Петровым в его работе «Трение в машинах и влияние на него смазывающей жидкости», вышедшей в 1883 году. В результате исследования движения жидкости при небольших скоростях в прямолинейной трубе круглого сечения была предложена зависимость
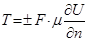 , (1.8)
, (1.8)
или
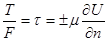 , (1.9)
, (1.9)
где Т – сила внутреннего трения; 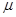 –динамический коэффициент вязкости, т.е. коэффициент, характеризующий сопротивляемость данной жидкости сдвигу. Величина, аналогичная коэффициенту сдвига в твердых телах; F – площадь поверхности соприкасающихся слоев;
–динамический коэффициент вязкости, т.е. коэффициент, характеризующий сопротивляемость данной жидкости сдвигу. Величина, аналогичная коэффициенту сдвига в твердых телах; F – площадь поверхности соприкасающихся слоев; 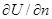 –градиент скорости (относительный сдвиг);
–градиент скорости (относительный сдвиг); 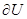 −абсолютный сдвиг (скорость смещения одного слоя относительно другого);
−абсолютный сдвиг (скорость смещения одного слоя относительно другого); 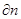 –расстояние между осями двух смежных слоев;
–расстояние между осями двух смежных слоев; 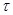 –напряжение сил внутреннего трения, возникающих по поверхности соприкосновения слоев.
–напряжение сил внутреннего трения, возникающих по поверхности соприкосновения слоев.
Знак «+» или «-» принимают в зависимости от знака градиента скорости 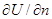 , чтобы
, чтобы 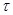 всегда было положительным.
всегда было положительным.
Соотношение 1.8 так же, как и 1.9, называется законом продольного внутреннего трения в жидкостях Ньютона. Поясним этот закон рисунком.

Как видите, трение в жидкости отличается от трения в твердых телах, где сила трения зависит от нормального давления и не зависит от площади трущихся поверхностей и скорости:
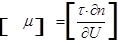 .
.
В системе СИ 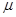 выражается в
выражается в 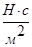 или Па·с.
или Па·с.
В системе МКГСС динамический коэффициент вязкости имеет размерность  .
.
В системе СГС за единицу динамической вязкости принят пуаз (Пз) в честь французского врача Пуазеля, исследовавшего законы движения крови в сосудах человеческого тела, 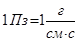 .
.
Соотношение между 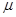 СИ и
СИ и 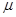 СГС следующее:
СГС следующее:
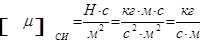 ,
,
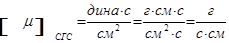 .
.
1Пз = 1 г/см·с = 0,001 кг/0,01 м·с = 0,1 кг/м·с = 0,1 Па · с,
т.е. 1Пз = 0,1 Па·с, 1Пз = 1 дина·с/см2 = 10-5 Н с/10-4м2 = 0,1Н·с/м2 = =0,1 Па·с.
Для пресной воды при t = 100С
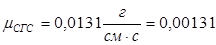 Па·с.
Па·с.
В расчетах часто применяют кинематический коэффициент вязкости 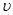 .
.
Связь между 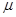 и
и 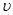 выражается зависимостью:
выражается зависимостью:
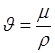 , (1.10)
, (1.10)
где 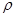 –плотность жидкости.
–плотность жидкости.
Размерность 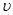 в системе МКГСС – м2/с, в системе СГС – см2/с, в системе СИ –м2/с.
в системе МКГСС – м2/с, в системе СГС – см2/с, в системе СИ –м2/с.
1см2/с = 1 стокс (ст). Для воды при t = 100С
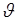 = 0,0131 см2/с = 0,0131 ст = 1,31 сст.
= 0,0131 см2/с = 0,0131 ст = 1,31 сст.
Глава вторая
ГИДРОСТАТИКА
2.1. Силы, действующие в жидкости.
Гидростатическое давление и его свойства
Силы, действующие в жидкости, могут быть подразделены на поверхностные и массовые.
Поверхностные силы действуют на поверхностях, отделяющих рассматриваемый объем жидкости от окружающей среды. К этой категории относятся силы гидравлического давления, являющиеся нормальными (как будет показано ниже), и силы внутреннего трения, являющиеся касательными.
Массовые силы действуют на каждую частичку рассматриваемого объема жидкости и поэтому пропорциональны его массе. К категории этих сил относятся сила тяжести и сила инерции. Массовые силы характеризуются ускорениями, которые они сообщают единице массы жидкости. Например, ускорение силы тяжести направлено вертикально вниз и равно g = 9,81 м/сек2.
Под влиянием воздействий этих сил в жидкости возникают механические напряжения. Чтобы выяснить характер этих напряжений и выявить законы их изменения рассмотрим некоторый объем жидкости (рис. 1), находящийся в равновесии под действием сил Р1, Р2 и т.д. Если рассечь мысленно этот объем произвольно выбранной плоскостью АВСД и отбросить его верхнюю часть, то для сохранения равновесия его нижней части необходимо к плоскости АВСД приложить силы, эквивалентные действию верхней отброшенной части на нижнюю.
Пусть сила Р представляет собой равнодействующую всех сил, которые определяют воздействие верхней части объема жидкости на нижнюю. Эта сила приложена в точке А плоскости АВСД, площадь которой 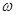 .
.
Тогда отношение Р/ 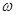 = рср представляет собой среднее гидростатическое давление на площадку
= рср представляет собой среднее гидростатическое давление на площадку  или среднее гидростатическое напряжение давления. Если
или среднее гидростатическое напряжение давления. Если  стремится к нулю, то отношение Р/
стремится к нулю, то отношение Р/  стремится к некоторому пределу, величина которого выражает напряжение давления в данной точке жидкости:
стремится к некоторому пределу, величина которого выражает напряжение давления в данной точке жидкости:
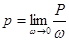 . (2.1)
. (2.1)
В гидравлике силу Р называют общей или суммарной силой давления на площадку (гидравлической силой), рср – средним гидростатическим давлением на площадку, а р – гидростатическим давлением в точке или просто гидростатическим давлением.
Поскольку в покоящейся жидкости касательные силы отсутствуют, гидростатическое давление является результатом действия нормальных сжимающих сил, т.е. поверхностных сил давления и массовых сил.
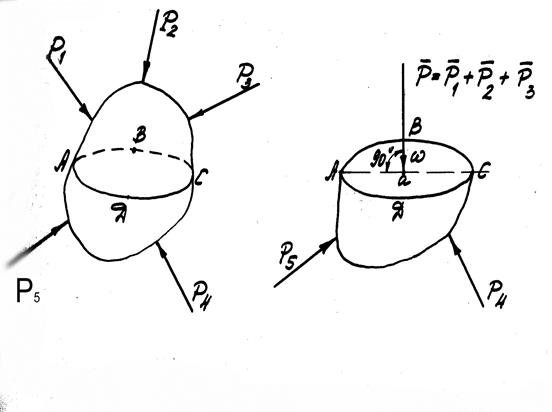
Рис.1
Гидростатическое давление имеет размерность напряжения (отношение силы к площади): в системе МКГСС – кгс/м2, а в системе СИ – н/м2, или 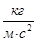 ; 1н/м2 = 1 Па (паскаль), 1·105 н/м2 называется баром (1бар=750,1 мм рт.ст.).
; 1н/м2 = 1 Па (паскаль), 1·105 н/м2 называется баром (1бар=750,1 мм рт.ст.).
Гидростатическое давление идеальной жидкости обладает тремя характерными свойствами, которые можно распространить и на давление реальных, но не очень вязких жидкостей.
1.Гидростатическое давление действует нормально к площадке, воспринимающей его, внутрь объема жидкости.
2.Гидростатическое давление в любой точке жидкости не зависит от ориентировки площадки, на которую оно действует, т.е. гидростатическое давление действует одинаково по всем направлениям.
3.Гидростатическое давление в точке зависит от ее координат в пространстве.
Очевидно, что по мере увеличения погружения в рассматриваемой точке под уровень, давление в ней будет возрастать и, наоборот, по мере уменьшения погружения – уменьшаться. Это свойство гидростатического давления можно записать в виде
р = f(x, y, z) . (2.2)
2.2. Дифференциальные уравнения равновесия
идеальной жидкости (уравнения Л. Эйлера)
 Выделим в покоящейся жидкости элементарный прямоугольный параллелепипед (рис.2), т.е. длины его ребер dx , dy , dz считаем бесконечно малыми величинами. Оси прямоугольных координат направим параллельно ребрам параллелепипеда. В центре тяжести каждой грани параллелепипеда приложим силу гидростатического давления, замещающую действие на нее окружающей массы жидкости. Эти силы согласно первому свойству гидростатического давления будут направлены по нормали внутрь параллелепипеда. Каждая из рассматриваемых сил равна произведению гидростатического давления в центре тяжести данной грани параллелепипеда на ее площадь.
Выделим в покоящейся жидкости элементарный прямоугольный параллелепипед (рис.2), т.е. длины его ребер dx , dy , dz считаем бесконечно малыми величинами. Оси прямоугольных координат направим параллельно ребрам параллелепипеда. В центре тяжести каждой грани параллелепипеда приложим силу гидростатического давления, замещающую действие на нее окружающей массы жидкости. Эти силы согласно первому свойству гидростатического давления будут направлены по нормали внутрь параллелепипеда. Каждая из рассматриваемых сил равна произведению гидростатического давления в центре тяжести данной грани параллелепипеда на ее площадь.
Обозначим гидростатическое давление в центре тяжести параллелепипеда (точка А) через р. Учитывая непрерывность изменения давления в жидкости, т.е. функциональную зависимость (2.2), найдем, что гидростатические давления в центрах тяжести граней параллелепипеда отличаются от давления в точке А соответственно на
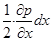 ;
; 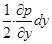 и
и 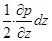 .
.
В связи с изложенным силы гидростатического давления будут равны:
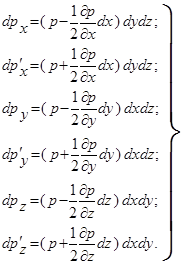 (2.3)
(2.3)
Кроме сил гидростатического давления (поверхностных сил) на рассматриваемый параллелепипед действуют массовые силы, непрерывно распределенные по его объему (в данном случае силы тяжести). Равнодействующую массовых сил dG можно представить как произведение ускорения g массовой силы на массу жидкости в объеме параллелепипеда:
dG=g·  ·dx·dy·dz, (2.4)
·dx·dy·dz, (2.4)
где 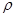 –плотность жидкости.
–плотность жидкости.
Полагаем, что плотность жидкости постоянна, т.е. 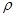 = const . Следовательно, жидкость рассматривается как несжимаемая.
= const . Следовательно, жидкость рассматривается как несжимаемая.
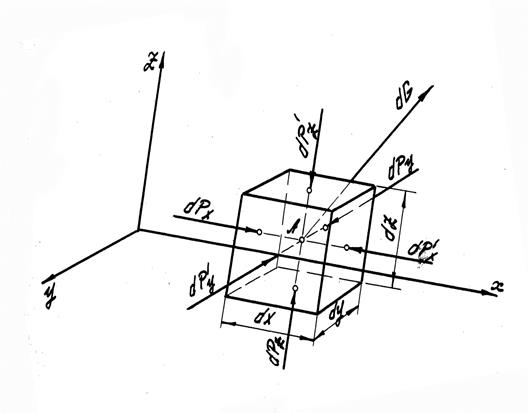
Рис.2
Обозначив проекцию ускорения g на оси О X , OY , О Z соответственно через X , Y , Z, получим выражения для проекции силы dG на эти оси:
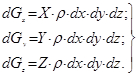 (2.5)
(2.5)
Параллелепипед находится в равновесии, поэтому суммы проекции сил на каждую координатную ось должны быть равны нулю. Запишем выражения сумм для каждой оси (О X , OY , О Z соответственно):
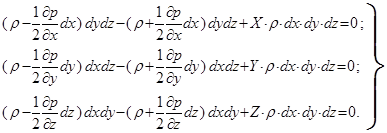 (2.6)
(2.6)
Раскрыв скобки и разделив каждое из уравнений на массу параллелепипеда 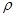 dxdydz, т.е. приведя каждый член уравнения к единице массы рассматриваемого объема жидкости, получим систему дифференциальных уравнений равновесия идеальной жидкости:
dxdydz, т.е. приведя каждый член уравнения к единице массы рассматриваемого объема жидкости, получим систему дифференциальных уравнений равновесия идеальной жидкости:
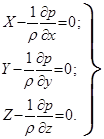 (2.7)
(2.7)
Эти уравнения впервые были выведены в 1755 году Л. Эйлером, поэтому их часто называют уравнениями Эйлера.
2.3. Интегрирование дифференциальных уравнений равновесия
Идеальной жидкости
Умножая уравнения (2.7) соответственно на dx , dy и dz и складывая их, получим
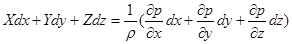 . (2.8)
. (2.8)
Поскольку р = f ( x , y , z ), выражение в скобках в правой части уравнения (2.8) есть полный дифференциал гидростатического давления, следовательно,
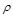 ( Xdx + Ydy + Zdz)= dp . (2.9)
( Xdx + Ydy + Zdz)= dp . (2.9)
Уравнение (2.9) есть основное уравнение гидростатики в дифференциальной форме.
Проинтегрируем уравнение (2.9) для случая, когда жидкость заключена в вертикальном цилиндрическом сосуде и находится в покое под действием силы тяжести и внешнего давления на ее свободной поверхности (рис. 3).

Рис.3
Горизонтальная плоскость XOY называется плоскостью сравнения.
Для рассматриваемого случая, составляющие единичной силы тяжести по координатным осям будут равны:
Х= 0; Y= 0; Z= - g, и отсюда
dp= - 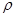 g·dz. (2.10)
g·dz. (2.10)
p= - 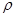 g·Z+C. (2.11)
g·Z+C. (2.11)
При р = р0 и Z = Z 0
C = p0 + 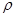 gZ0,
gZ0,
поэтому уравнение (2.11) примет вид
p = - 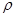 g · Z + р 0 +
g · Z + р 0 + 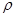 gZ0 , (2.12)
gZ0 , (2.12)
или
p = p0 + 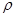 g(Z0 -Z) = p0 +
g(Z0 -Z) = p0 + 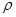 gh, (2.13)
gh, (2.13)
p = p0 + 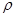 gh, (2.14)
gh, (2.14)
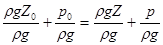 , (2.15)
, (2.15)
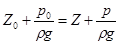 . (2.16)
. (2.16)
Уравнения (2.14) и (2.15) – это две разновидности основного уравнения гидростатики.
Уравнение (2.14) является математическим выражением закона распределения гидростатического давления в жидкости: величина гидравлического давления в некоторой точке, погруженной на глубину h относительно свободной поверхности, равна сумме внешнего давления на свободную поверхность жидкости р0 и давления от веса столба жидкости с площадью основания, равной единице, и высотой, равной глубине погружения h рассматриваемой точки.
Помимо этого уравнение (2.14) показывает, что внешнее давление р0, которое действует на поверхность жидкости, передается всем точкам жидкости без изменения. В этом заключается суть закона Паскаля.
2.4. Полное (абсолютное) и манометрическое давление.
Дата: 2019-11-01, просмотров: 383.