Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

             

а) под влиянием одного фактора

S – критерий тенденций Джонкира Миним. с=3 и N≥2, 2, 2 Максим. с=6 при N≤10, 10, 10 L – критерий тенденций Пейджа Миним. с=3 и N=2 Максим. с=6 и N=12 Однофакторный дисперсионный анализ Фишера. а) Не менее трех градаций исследуемого фактора и не менее двух испытуемых в каждой градации б) Равенство дисперсий в каждой ячейке дисперсионного комплекса в) При условии нормальности распределения результативного признака б) под влиянием двух факторов одновременно Двухфакторный дисперсионный анализ Фишера. а) Не менее двух градаций каждого исследуемого фактора б) В каждой ячейке комплекса не менее двух испытуемых в) Равенство дисперсий в каждой ячейке дисперсионного комплекса г) Комплекс должен представлять симметричную систему: каждой градации фактора А должно соответствовать одинаковое количество градаций фактора Б д) Факторы А и Б должны быть независимы е) При условии нормальности распределения результативного признака

 

 

Контрольные вопросы:

1. Что такое статистическая гипотеза?

2. В чем состоит различие между направленными и ненаправленными статистическими гипотезами?

3. Какие бывают ошибки при проверке статистических гипотез?

4. Что такое уровень значимости вывода?

5. Каким образом делается вывод при проверке статистических гипотез?

6. Что такое критерий различий?

7. Приведите классификацию критериев различий.

8. В чем различие между односторонними и двусторонними критериями?

9. От чего зависит выбор критерия различий?

 

Самостоятельное практическое задание: для каждого критерия различий придумайте пример психологического исследования, в котором статистическую гипотезу необходимо было проверить с помощью данного критерия.

Материалы для изучения темы:

а) основная литература:

1. Ермолаев О. Ю. Математическая статистика для психологов. — М., 2008. — Стр. 58-70.

2. Кутейников А.Н. Математические методы в психологии. – СПб, 2008. — Стр. 50-59.

3. Наследов А. Д. Математические методы психологического исследования: Анализ и интерпретация данных. — СПб., 2007. — Стр. 93-113.

4. Сидоренко Е. В. Методы математической обработки в психологии. — СПб.,2004. — Стр. 24-38.

б) дополнительная литература:

1. Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии. — М., 1976. — Стр. 246-264.

2. Суходольский Г. В. Основы математической статистики для психологов. — СПб., 1998. — 291-294.

 

Тема 6. Выявление различий в уровне исследуемого признака

Параметрический критерий t Стьюдента для сравнения результатов количественного измерения: назначение критерия, его описание, область применения, алгоритм применения для независимых выборок. Критерий Фишера. Поправка Снедекора.

Непараметрические критерии. Критерий Розенбаума: назначение критерия, его описание, область применения, алгоритм применения. Критерий Манна–Уитни: назначение критерия, его описание, область применения, алгоритм применения. Критерий тенденций Крускала-Уоллиса назначение критерия, его описание, область применения, алгоритм применения. Критерий тенденций Джонкира: назначение критерия, его описание, область применения, алгоритм применения.

Методические рекомендации к изучению темы

При изучении данной темы необходимо обратить внимание на то, что критерий Стьюдента применяется для сравнения любых двух параметров распределений, однако в лекциях приведены формулы лишь для сравнения среднего арифметического значения и стандартного отклонения. Внимательно изучите ограничения в применении критерии Стьюдента. Обратите внимание, что одно из ограничений касается нормальности распределения признака в выборках.

После изучения материала лекции ответьте на контрольные вопросы, ответы занесите в конспект.

Материалы лекции.

Параметрический критерий Стьюдента для сравнения независимых выборок

Назначение критерия

Критерий Стьюдента применяется:

А) для сравнения любых двух параметров распределений или проверки гипотез о случайности различий между параметрами (Н₀);

Б) для интервального оценивания (является ли параметр, полученный на выборочной совокупности, параметром генеральной совокупности);

В) для оценки статистической значимости мер связи (коэффициентов корреляции).

Ограничения в использовании критерия:

1. Критерий Стьюдента применяется для сравнения параметров признаков, измеренным по интервальной или пропорциональной шкалам.

2. Распределение признака должно быть нормальным.

3. Ограничений по объему выборки нет

 

Алгоритм расчета критерия для независимых выборок:

 

1. Для каждой выборки отдельно рассчитываются параметры распределений. Таким образом, мы имеем:

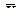 — среднее арифметическое значение признака в выборке 1;

 — среднее арифметическое значение признака в выборке 2;

σ₁ — стандартное отклонение признака в выборке 1;

σ₂ — стандартное отклонение признака в выборке 2;

N₁ — объем (количество испытуемых) выборки 1;

N₂ — объем (количество испытуемых) выборки 2.

А) Выборки разного объема N₁≠ N₂

2) Вычисляется величина, характеризующая различия изменчивости результатов в двух выборках:

      

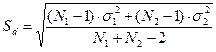
3) Находим расчетное (эмпирическое) значение критерия Стьюдента по следующей формуле:

      

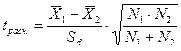
4) Для того, чтобы найти по таблице критических значений табличное значение критерия, находим число степеней свободы по формуле:

      

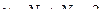
Б) Выборки одинакового объема N₁= N₂ = N (после расчета параметров распредлений можно сразу вычислить расчетное значение критерия)

 2) Находим расчетное (эмпирическое) значение критерия Стьюдента по следующей формуле:

      

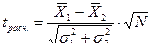
3) Для того, чтобы найти по таблице критических значений табличное значение критерия, находим число степеней свободы по формуле:

      

В) Правило вывода (правило принятия решения)

       Критические (табличные) значения критерия Стьюдента находятся по таблице критических значений для этого критерия в зависимости от числа степеней свободы.

       Если 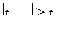, то Н₀ отвергается, то есть сравниваемые параметры (средние арифметические в данном случае) статистически различаются.

       Если 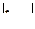 < 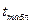, то Н₀ принимается, то есть сравниваемые параметры (средние арифметические в данном случае) статистически не различаются.

 

       Возможны случаи, когда значимость различий между средними обусловлена не различием средних арифметических генеральных совокупностей, а различием их дисперсий. Результат сравнения средних в этом случае будет искажен. Поэтому при использовании критерия Стьюдента для сравнения средних арифметических рекомендуется всегда оценивать и расхождение между дисперсиями.

Сравнить дисперсии можно двумя способами:

       А) для нормальных распределений большого объема можно использовать критерий Стьюдента и оценить различия между стандартными отклонениями.

                   ,

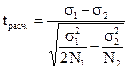где σ₁ и σ₂ — стандартные отклонения 1-й и 2-й выборок;

N₁ и N₂ — число испытуемых в 1-й и 2-й выборках.

Правило принятия решения:

       Если , то различия между дисперсиями статистически значимы. Если 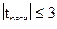, то дисперсии статистически не различаются.

           

Б) Для малочисленных выборок из нормально распределенной генеральной совокупности используется параметрический критерий Фишера.

Назначение критерия

Критерий Фишера применяется:

а) для сравнения двух дисперсий;

б) для проверки гипотезы о значимости коэффициентов детерминации;

в) для проверки гипотезы об однородности ряда средних арифметических значений.

Ограничения в использовании критерия: критерий применяется для сравнения признаков, измеренных в интервальной или пропорциональной шкале.

Критерий Фишера рассчитывается по следующей формуле:

                   ,

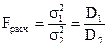где σ₁ и σ₂ — стандартные отклонения 1-й и 2-й выборок;

D₁ и D₂ — дисперсии в 1-й и 2-й выборках.

В формуле критерия Фишера в числитель дроби всегда ставится большая величина, то есть σ₁ > σ₂ или D₁ > D₂.

Правило принятия решения:

       Расчетное значение критерия Фишера необходимо сравнить с критическим (табличным) значением (см. таблицу критических значений критерия Фишера), которое находится в зависимости от двух значений — числа степеней свободы для каждой выборки. Число степеней свободы находится по следующим формулам:

                   ν₁ = N₁ – 1 и  ν₂ = N₂ – 1

       Если F_расч. > F_{критич.}, то различия между дисперсиями статистически значимы. Если F_расч. ≤ F_{критич.}, то дисперсии статистически не различаются.

 

       Статистически значимое различие дисперсий указывает на то, что генеральные совокупности, из которых взяты выборки, также имеют разные дисперсии. В этом случае рекомендуется при сравнении средних арифметических значений с помощью критерия Стьюдента вводить в критерий поправку по Снедекору.

 

Поправка Снедекора

       Критерий Стьюдента рассчитывается обычным способом. Поправка Снедекора заключается в том, что расчетное значение сравнивают не с обычным критическим значением, а с иным, которое повышает это критическое значение.

       Если сравниваются выборки равного объема, то есть N₁= N₂=N, то табличное значение находят для числа степеней свободы, вычисленное по формуле: ν = N – 1. 

       Если сравниваются выборки разного объема, то вычисляют среде взвешенное табличное значение критерия Стьюдента следующим образом.

       Для каждой из выборок находят свое число степеней свободы по формулам:                ν₁ = N₁ – 1 и ν₂ = N₂ – 1.

       В зависимости от ν₁ по таблице критических значений находят t_{табл. 1} и в зависимости от ν₂ находят t_{табл. 2}.

       Далее вычисляется критическое значение критерия, с которым и будет сравниваться расчетное значение:

                   ,

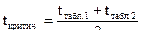где t_{табл. 1} — табличное значение критерия Стьюдента для 1-й выборки;             

  t_{табл. 2} — табличное значение критерия Стьюдента для 2-й выборки.