Для интегрирования в Scilab имеется универсальная функция intg:
[s,er]=intg(a,b,f,er1,er2),
где: a , b– пределы интегрирования;
f – имя подынтегральной функции, которая может быть задана с помощью внешней функции или в виде набора дискретных точек и должна быть непрерывной;
er 1 и er 2– необязательные параметры – абсолютная и относительная погрешности интегрирования. Если погрешность вычисления интеграла отсутствует, то вычисление проводится с погрешностью, установленной по умолчанию (значение er 1 равно 1. D -8, а значение er 2 равно 1.D-14).
Функция intgвозвращает значение интеграла (s) и оценку абсолютной ошибки вычислений (er).
Внешнюю функцию можно задать функцией deffили function:
· если f – функция, то её определение должно иметь видy = f ( t );
· если f – список, то этот список должен быть описан как: list ( f , x 1, x 2,…).
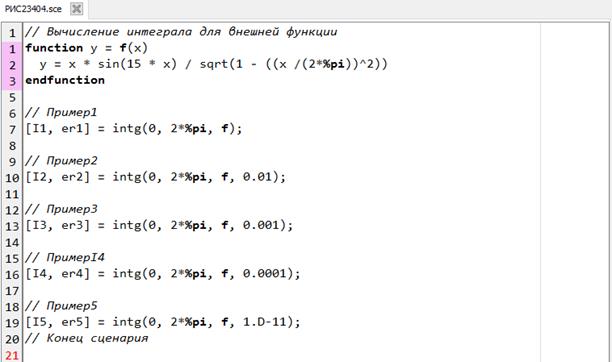
Рассмотрим несколько примеров (рис.2.3.4-4).
|
-->// Загрузка сценария РИС2 3404 и выполнение функции intg
--> exec('РИС23404.sce ');
--> disp([" I ", " er "], ...
> [I1, er1], [I2, er2], [I3, er3], [I4, er4], [I5, er5]);
! I er !
-3.58957861311877350 0.00000000001621547
-3.58957861320974690 0.00001678794315296
-3.58957862082392730 0.0015909785599586
-3.58957862082391800 0.00159097855998436
-3.58957861311831690 0.00000000781318699
|
Рис.2.3.4-4. Вычисление определенных интегралов функциейintg
Точность полученного результата зависит от заданной абсолютной погрешности. Поэтому очевидно, что в Примере1 и Примере5 обеспечена максимальная точность.
Опишем подынтегральную функцию y=cos(x)2/(1-x)в функции fi(x) и вычислим значение определенного интеграла (с пределами a=2 и
b=6) сначала с помощью функции intg, а затем – функции inttrap, разбив при этом отрезок интегрирования на 5, 10 и 20 частей (рис.2.3.4-5).
 --> // Сравнение вычисления интеграла функциями intg и inttrap по точности
-->
-->// Описание подынтегральной функции
-->deff('[y] = fi(x)', 'y = cos(x).^2 ./ (1-x)')
-->
-->a = 2; b = 6;
--> // Вычисление интеграла с помощью функции intg
--> [s,ir] = intg(a, b, fi)
ir =
5.844D-10
s =
-0.8781216
-->
--> // Вычисление интеграла с помощью функцииinttrap
--> // s1–5 точек (h1=0.8); s2–10 (h2=0.4); s3–20 (h3=0.2);
--> h1 = 0.8; x = a:h1:b; y = fi(x); s1 = inttrap(x, y)
--> h2 = 0.4; x = a:h2:b; y = fi(x); s1 = inttrap(x, y)
--> h3 = 0.2; x = a:h3:b; y = fi(x); s1 = inttrap(x, y)
--> z=[h1,s1; h2,s2; h3,s3]
z =
0.8 -0.8490697
0.4 -0.8711676
0.2 -0.8764039
|
Рис.2.3.4-5. Влияние величины шага на точность интегрирования
Из полученных результатов (рис.2.3.4-5) следует, что, если значение интеграла, полученное с использованием функции intg можно принять практически за точное значение (относительная погрешность 5.844D-10), то с помощью функции inttrap, использующей таблицу значений подынтегральной функции, мы только приблизились к этому значению. При этом из полученных результатов явно следует, что чем меньше значение шага интегрирования, тем точнее результат. А поскольку величина шага влияет на количество используемых узловых точек, то становится очевидным, что увеличение числа, используемых в расчете узловых точек приводит к получению более точного значения интеграла.
Рассмотрим несколько задач.
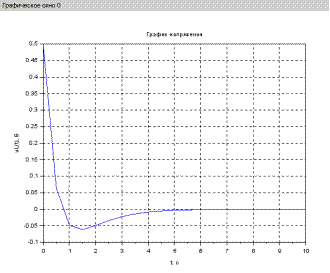
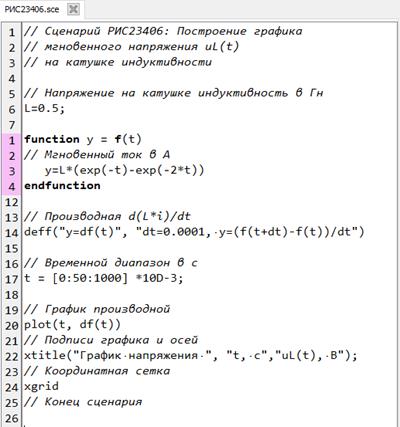
Построить график мгновенного напряжения uL ( t ) на катушке индуктивности L =0,5 Гн в интервале [0 1000] м c , если i ( t )= exp (- t )- exp (2 t )
(рис. 2.3.4-6).
|
L=0.5 Гн
t=[0:50:1000]* 10D-3;
|
|
exec('РИС23406.sce', 0)
| |
Рис.2.3.4-6. Связь между мгновенным током и напряжением в катушке индуктивности
Решим несколько задач.
Определить мощность, выделяемую в резисторе сопротивлением R =1Ом, если через него протекает ток гармонической формы с мгновенными значением i = sin ( t )(Рис.2.3.4-7. ).
В ТЭЦ среднюю мощность Pможно выразить формулой: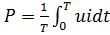 
,
где T – период, u– мгновенное напряжение, i– мгновенный ток.
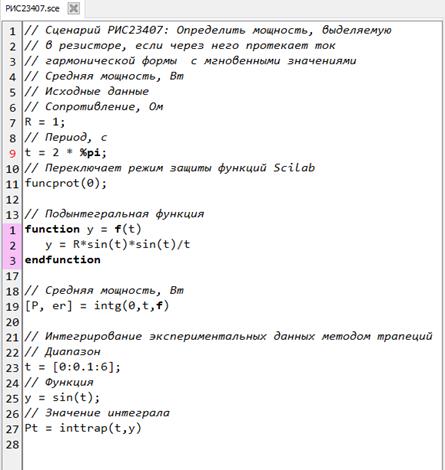
exec(РИС23407.sce', 0)
er =
1.339D-11
P =
1.5571783
Pt =
0.0397965
| 
R = 1 ом
t=2  c
|
Рис.2.3.4-7. Определение мощности, выделяемая в резисторе
2.3.5. Контрольные вопросы
1) Какой встроенной функцией системы Scilabвычисляется производная в заданной точке?
2) Какое назначение и какой формат функции numderivativeиспользуется.
3) Как осуществляется вычисление производной от функции, заданной аналитически?
4) Как формулируется постановка задачи численного интегрирования в Scilab?
5) Какая функция позволяет получить производную от полинома в явном виде?
6) Что называется, аппроксимированным дифференцированием?
7) Как осуществляется вычисление определенных интегралов в Scilab?
8) Назначение функции inttrap ( x , y )?
9) Что возвращает функция inttrap ( x , y ), если y ( x ) – матрица?
10) Можно ли использовать функцию inttrap, если узлы по оси х - не равноотстоящие?
11) Какая функция Scilab позволяет вычислить определенный интеграл с заданной точностью?
12) Какой численный метод заложен в функции integrate?
13) Какие существуют способы задания подынтегральной функции при вычислении определенного интеграла с использованием функции integrate?
14) Как задать допустимую погрешность вычисления определенного интеграла?
15) С какой точностью производится вычисление определенного интеграла, если погрешность не задана?
2.4. Решение нелинейных уравнений
2.4.1. Постановка задачи решения
нелинейных уравнений
В общем виде нелинейное уравнение (НУ) можно представить как
f( x )=0. В зависимости от вида элементарных функций, входящих в состав функции нелинейного уравнения, различают алгебраические и трансцендентные уравнения.
Алгебраическими уравнениями называются уравнения, в которых значение функции f(x) представляет собой полином n-й степени (n≥2). Всякое неалгебраическое уравнение называется трансцендентным. Функция f(x) в таких уравнениях содержит хотя бы одну из следующих элементарных функций: показательную, логарифмическую, тригонометрическую или обратную тригонометрическую.
Решением уравнения f(x)=0 является совокупность корней Х, при которых уравнение обращается в тождество f(Х)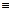 
0. Однако, точные значения корней могут быть найдены аналитически только для некоторого ограниченного типа уравнений. Еще меньше возможностей для получения точного решения у трансцендентных уравнений. Таким образом, задача нахождения точных значений корней не всегда корректна. Например, если коэффициенты уравнения являются приближенными числами, точность вычисленных значений корней заведомо не может превышать точности исходных данных. Эти обстоятельства заставляют рассматривать возможность отыскания корней уравнения с ограниченной точностью (приближенных значений корней).
Процесс численного решения нелинейного уравнения состоит из двух этапов:
1) отделение корней уравнения (локализация каждого корня нелинейного уравнения на отдельном отрезке);
2) уточнение каждого корня на выбранном отрезке с заданной точностью.
Этап отделения корней нужен для того, чтобы, во-первых, убедиться, что данное уравнение вообще имеет корни, а во-вторых, необходим для выбора начального значения при использовании численных методов. Важно, что численные методы при этом применимы только тогда, когда на выделенном отрезке существует единственный корень.
Для отделения корней нелинейных уравнений применяются графический и аналитический методы. При применении графического метода в области допустимых значений функции (левой части уравнения) строится ее график и визуально определяются отрезки, имеющие единственное пересечение с осью абсцисс О X. Использование аналитического метода основывается на теореме о существовании и единственности корня на отрезке [24]. Согласно этой теореме надо найти такие отрезки, на концах которых функция f(x)имеет разные знаки, а первая производная непрерывна и не меняет свой знак (то есть функция монотонна).
Для уточнения корней с заданной степенью точности существуют множество классических численных методов (метод Ньютона, метод хорд, метод итераций, метод половинного деления и многие другие, а также их модификации) [22].
Задача нахождения корня уравнения с заданной точностью ε ( ε>0) считается решенной за n итераций, если найдено приближенное значение xn, которое отличается от точного значения корня x* не более чем на значение e: | x *-xn|≤ε .
Рассмотрим средства Scilab, используемые для решения нелинейных уравнений.
2.4.2. Решение нелинейных уравнений
средствами Scilab
Итак, первым этапом решения нелинейных уравнений является исследование функции решаемого НУ, в результате чего в области допустимых значений функции выявляются такие отрезки (или отрезок), которые содержат только один корень.
Рассмотрим этап отделения корней средствами Scilab на примере решения нелинейного уравнения 2 x –4 x =0.
Отделение корня нелинейного уравнения целесообразно вначале произвести графически. Из графика функции f ( x )=2 x –4 x(рис. 2.4.2-1) следует, что уравнение имеет два действительных корня, принадлежащих отрезкам [0;1] и [3.5;4.5].
-->// Графическое отделение корня нелинейного уравнения
--> // Загрузка сценария РИС2421 и его выполнение
-->
-->clear
--> exec('РИС2421.sce', 0);
|
Рис.2.4.2-1. Графическое отделение корней нелинейного уравнения 2 x –4 x =0
Проверим на выбранных отрезках выполнение аналитических условий существования и единственности корня (рис.2.4.2-2).
-->//Аналитическое отделение корня нелинейного уравнения
-->//Загрузка сценария РИС2422 и выполнение функций f ( x ) и f 1( x )
-->
--> clear
--> a = 0; b = 5; h = 0.5;
--> exec('РИС2422.sce', 0);
-->x = a : h : b; // Вектор аргумент x
-->fx = f(x); f1x = f1(x); // Вектор функций f и 1-й производной f 1
--> disp([x; fx; f1x]', [" x", " fx", " f1x "]);
! x fx f1x !
0. 1. -3.3068528194400546
0.5 -0.5857864376269049 -3.01974185653145270
1. -2. -2.61370563888010920
1.5 -3.17157287525380970 -2.03948371306290530
2. -4. -1.22741127776021890
2.5 -4.34314575050761940 -0.0789674261258111
3. -4. 1.5451774444795623
3.5 -2.68629150101523880 3.84206514774837780
4. 0. 7.09035488895912460
4.5 4.62741699796952230 11.6841302954967560
5. 12. 18.1807097779182490
|
Рис. 2.4.2-2. Отделение корня нелинейного уравнения
Из полученной таблицы, содержащей значения аргумента, функции и производной, следует, что условия существования и единственности корня выполняются на отрезках [0;0.5] и [3.5;4] (на концах каждого из этих отрезков функция имеет противоположные знаки, а ее производная на каждом из этих отрезков знакопостоянна).
Для решения нелинейных уравнений в среде Scilab используется функция fsolve, предназначенная для нахождения вещественных корней уравнений вида f (х)=0, использующая модификацию гибридного метода Пауэлла [13]. Хотя здесь и в дальнейшем fsolveназываем функцией, следует понимать, что fsolveпо своей сути является решателем, объединяющим под этим именем несколько алгоритмов.
Метод Пауэлла является методом локального поиска, поэтому очень важно правильно произвести выбор начального приближения, а по окончании поиска корня проверить индикатор завершения и остаточное значение для того, чтобы убедиться, что в результате выполнения функции получено правильное решение.
Функция fsolveимеет следующие основные форматы:
fsolve(x0,f)
[х,fx,id]=fsolve(x0,f,fp,er2),
где: х0 – начальное приближение к корню;
f – указатель на внешнюю функцию f ( x )уравнения f (х)=0;
fp– указатель на внешнею функцию fp ( x ) (необязательный параметр), представляющую производную от функции f ( x ) (при решении систем нелинейных уравнений fp– это Якобиан [13]);
er 2 – относительная погрешность (необязательный параметр) по умолчанию принимает значение 1. d -10, и определяет условие проверки сходимости;
х и fx – выходные параметры функции fsolve– значение корня уравнения, вычисленное с заданной относительной погрешностью er 2 и значение функции в точке корня;
id – индикатор (необязательный параметр), показывающий при каких условиях произошло прекращение итерационного процесса поиска корня.
Индикатор id может иметь следующие значения:
0 – неверные входные параметры;
1 – найдены значения корней с заданной точностью tol(или с
погрешностью, принятой по умолчанию);
2 – допустимое количество вызовов fдостигнуто;
3 – er 2 слишком мало, поэтому дальнейшие приближения
невозможны;
4 – итерации не дают результата (корней нет).
При использовании первого формата fsolveпроисходит вычисление и вывод корня уравнения, как значение переменной ans, а при использовании второго– значение корняx и значение функции в точке корня fx.
На рис.2.4.2-3 приведен пример уточнения корня нелинейного уравнения на отрезке [0;1] с использованием функции fsolve, где в качестве начального приближения к корню выбрано значение 0.
 --> // Загрузка сценария РИС2423, содержащего описание функции f(x)
--> // Уточнение корня нелинейного уравнения на отрезке[0;1]
-->exec('РИС2423.sce', 0);
-->
--> // Первый способ
-->fx = f(x);
--> [x, fx] = fsolve(0, f) // Начальное приближение х0 = 0
-->disp([x, fx], [" x ", " fx "]);
! xfx !
0.30990693238069056 0.
-->
--> // Второй способ
-->x = fsolve(0, f); fx = f(x);
-->disp([x, fx], [" x ", " fx "]);
! x fx!
0.30990693238069056 0.
|
Рис. 2.4.2-3. Уточнение корня уравнения с использованием функции fsolve
При обращении к функции fsolveможет использоваться и один выходной параметр – х, тогда происходит только вычисление корня, а значение функции может быть по необходимости вычислено позже.
В следующем примере показано решение нелинейного уравнения
ex/5–2(x-1)2=0, иллюстрирующее возможность использования функции fsolve для решения НУ, имеющего несколько корней, при условии, что для каждого из коней задается свое начальное приближение.
Предположим, что предварительно проведено графическое отделение всех корней уравнения ex /5–2( x -1) 2 =0 (рис. 2.4.2-4), из которого следует, что уравнение имеет три корня, принадлежащие соответственно следующим отрезкам: x 1 ?[0.5;1], x 2 ?[1.5;2], х3?[5;5.5].
|
-->// Загрузка сценария РИС2424 . sce , содержащего описание функции f ( x ),
-->// отображение графика и
--> // выполнение функции fsolve с различными начальными приближениями
-->
-->clear
-->exec('РИС2425.sce', 0);
--> // 1-ый этап: Отделение корней графическим способом:
-->x = 0 : 0.2 : 5.5;
-->y = yf(x); // Левая часть НУ
-->y1 =x * 0; // y 1 используется для выделения оси Ох
--> plot(x, y, x, y1)
--> xtitle('', 'X', 'Y(X)');
-->xgrid();
|
|
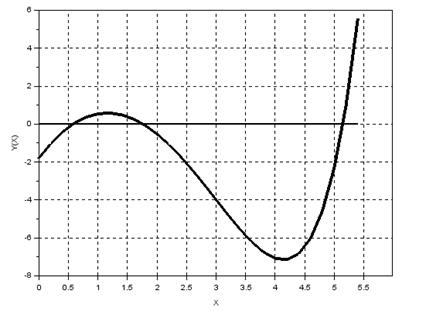
--> // Из графика видно, что уравнение имеет три корня,
--> // принадлежащие отрезкам: x 1 ?[0.5;1], x 2 ?[1.5;2], х3?[5;5.5]
-->//Выбор начальных приближений: x 1 = 0.5, x 2 = 2, x 3 = 5
-->
--> // 2-ый этап: Уточнение корней:
--> // 1-й способ: вычисление каждого корня уравнения отдельным
--> // обращением к функции fsolve
-->xx(1) = fsolve(0.5, yf); xx(2) = fsolve(2, yf); xx(3) = fsolve(5, yf);
-->yy = yf(xx); xy = [xx'; yy']'
xy =
0.5778406 -3.220D-15
1.7638701 1.554D-15
5.1476865 0.
-->
--> // 2-й способ: вычисление корней уравнения с использованием
--> // вектора начальных приближений
--> [xx,yy] = fsolve([0.5; 2;5], yf);
-->xy = [xx'; yy']'
xy =
0.5778406 -3.220D-15
1.7638701 1.554D-15
5.1476865 0.
|
Рис. 2.4.2-4. Отделение корней нелинейного уравнения графическим методом и уточнение его корней с использованием функции fsolve
На рис. 2.4.2-4 реализовано решение заданного нелинейного уравнения с использованием функции fsolve двумя способами. В первом случае функцию fsolve используют трижды, то есть по числу отделенных корней уравнения. При этом для каждого корня задается свое начальное приближение. Второй способ иллюстрирует возможность задания начальных приближений к корням в виде вектора, что и позволяет выполнить функцию fsolve всего один раз.
Приведем еще один пример использования функции fsolve, содержащей третий (необязательный) выходной параметр – индикатор (рис.2.4.2-5). Для этого используем нелинейное уравнение sin(x)+2=0, для которого заранее известно, что оно не имеет корней. В результате выполнения значение индикатора приняло значение 4, что говорит о том, что корень не найден, а в качестве результата выведено значение переменной, обеспечивающее максимальное приближение к корню.
|
|
--> // Загрузка сценария РИС2425, содержащего описание функции f ( x)
--> // Уточнение корня нелинейного уравнения и
--> // использование индикатора для проверки наличия корня
-->
-->exec('РИС2425.sce', 0);
-->
--> [xx, yy, id] = fsolve(0, fd)
id =
4.
yy =
1.0000001
xx =
-1.5703125
|
Рис. 2.4.2-5. Решение уравнения не имеющего корней
Функция fsolve может быть использована для решения как трансцендентных, так и алгебраических уравнений. Правая часть алгебраических уравнений представляет собой полином вида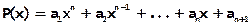 
. Однако, для вычисления корней полинома, как уже говорилось в п.2.1.1, чаще используется функция roots, так как эта функция вычисляет все корни, действительные и комплексные. Перед использованием roots создается список коэффициентов (даже нулевых), затем выполняется функция poly(a,'x','с'). Решим в качестве примера одно и тоже алгебраическое уравнение x5-x3+1=0 с использованием функций fsolve и roots, построив предварительно график функции левой части уравнения(рис. 2 4.2-6).
--> deff('[f] = y(x)', 'f = x^5 - x^3 + 1')
--> x = -2:0.1:2; f = y(x);
--> plot(x, f)
-->xtitle('X','Y');
-->xgrid();
|
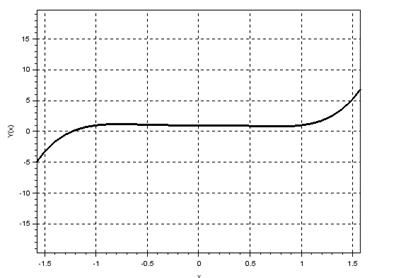
| --> // Решение алгебраического уравнения с помощью функции fsolve --> X = fsolve(-1.5, y) X = -1.2365057 |
| --> --> // Решение алгебраического уравнения с помощью функции roots -->Х = roots(poly([1 0 0 -1 0 1], 'x', 'c')) Х = -1.2365057 0.9590477 + 0.428366i 0.9590477 - 0.428366i -0.3407949 + 0.7854231i -0.3407949 - 0.7854231i |
Рис. 2.4.2-6. Уточнение корней уравнения с использованием
функций fsolveи roots
Из графика (рис. 2.4.2-6) видно, что уравнение имеет один действительный корень. Этот корень и был найден функцией fsolve. Решение этого же уравнения функцией roots показало, что кроме вещественного корня уравнение имеет еще несколько мнимых корней. Именно поэтому для вычисления всех корней полинома целесообразнее использовать функцию roots.
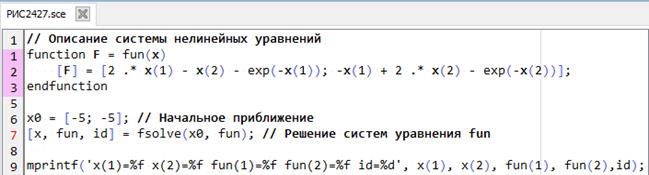
Функция fsolve может решать также и системы нелинейных уравнений от двух переменных. Рассмотрим следующий пример:решить систему нелинейных уравнений
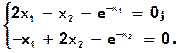
Решениепроведем при начальных значениях неизвестных x0=[-5,5].
Создадим sce-файл для вычисления значений F(x), в котором левые части уравнений системы представлены в виде элементов вектора, а начальные приближения к неизвестным x и обращение к функции fsolve содержатся в том же сценарии, записанном в файле РИС2427.sce (рис.2.4.2-7).
|
|
-->// Решение системы уравненийфункцией fsolve
-->// Загрузка и выполнение сценария РИС2429. sce
-->
--> clear
-->exec('РИС2427.sce', 0);
x(1)=0.567143 x(2)=0.567143 fun(1)=0.000000 fun(2)=0.000000 id=1
|
Рис. 2.4.2-7. Решение системы нелинейных уравнений функцией fsolve
Решение системы уравнений позволило за конечное число итераций (id =1) получить ее корни, которые при подстановке в заданную систему уравнений обращают уравнения в тождество. Поскольку точность вычислений не была задана, то они проводились с погрешносью, принятой по умолчанию.
2.4.3 Контрольные вопросы
1) Что является нелинейным уравнением?
2) Этапы численного решения нелинейных уравнений?
3) Как осуществляется графическое отделение корней нелинейного уравнения средствами Scilab?
4) Как осуществляется аналитическое отделение корней нелинейного уравнения средствами Scilab?
5) Какие основные идеи заложены в методе Пауэлла для нахождения корней нелинейных уравнений?
6) Какие имеются способы задания нелинейных уравнений при их решении с использованием функции fsolve?
7) Каково назначение и формат функции fsolve?
8) Каково назначение и формат функции poly?
9) Каково назначение и формат функции roots?
10) Что является решением функций fsolve и roots?
11) Какие алгоритмы используются в функции fsolve?
12) Какие алгоритмы используются в функции roots?
13) Каким образом необходимо задать исходные данные для решения систем нелинейных уравнений?
2.5. Решение обыкновенных
дифференциальных уравнений
2.5.1. Постановка задачи решения
обыкновенных дифференциальных уравнений
Дифференциальными уравнениями описываются практически все физические процессы, которые используются в технических приложениях. Аналитически может быть решено только ограниченное число дифференциальных уравнений. Тогда как численные методы могут давать приближенное решение практически любого дифференциального уравнения.
Обыкновенным дифференциальным уравнением (ОДУ) является уравнение, которое содержит независимую переменную, зависимую переменную и производные зависимой переменной. Таким образом, ОДУ
1-го порядка имеет следующий вид:
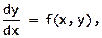
где xи y – независимая и зависимая переменные, соответственно.
Такое ОДУ первого порядка представлено в виде, разрешенном относительно производной y '= f ( x , y ).
Для решения ОДУ первого порядка, в соответствии с задачей Коши, должны быть заданы начальные условия его решения – y(x0)=y0. Тогда решением ОДУ является функция y= f (x), которая будучи подставленной в исходное уравнение, обратит его в тождество, при этом будут выполняться и начальные условия.
Задача Коши для решения ОДУ n-го порядка
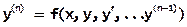
формулируется аналогично, при этом в качестве начальных условий должны быть заданы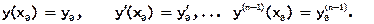 
При его решении выполняется ряд подстановок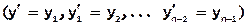 
, в результате которых ОДУ n-го порядка заменяется системой из n обыкновенных дифференциальных уравнений 1-го порядка:
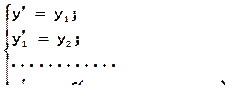
Результатом решения ОДУ численными методами является таблица значений y = y (x) на некотором заданном множестве значений аргументах. Поэтому при постановке задачи численного решения ОДУ наряду с начальными условиями x 0 , y 0необходимо задать область решения – отрезок интегрирования [a;b], где a=x0, и шаг изменения аргумента – h (шаг интегрирования).
Для получения численного решения ОДУ используются различные методы Рунге-Кутты [24],которые различаются порядком. Чем выше порядок метода, тем точнее решение, полученное при равном шаге интегрирования.
В этом разделе описываются некоторые средства системы Scilab, предназначенные для решения обыкновенных дифференциальных уравнений.
Дата: 2019-11-01, просмотров: 530.
