Версия системы Scilab 6.01, к сожалению, не позволяет получить аналитических выражений производных от функции f ( x ). Однако в ней имеется функция Scilab numderivative, предназначенная для вычисления значений производных 1-го или 2-го порядка в заданных точках от аналитических функций. Эта функция имеет следующие форматы:

numderivative( f , x )

J =numderivative( f , x )

J=numderivative(f,x,h)

h=numderivative(f,x,h,order)

[J,H]=numderivative (f,x,h,order).

Входные параметры:

f – функция или список функций, от которых берутся производные;

х – вектор значений независимых переменных, в которых вычисляются производные;

h– шаг, используемый в конечно-разностных приближениях. Если h не указан, то шаг по умолчанию вычисляется в зависимости от х и порядка. Если h-матрица 1х1, то она расширяется до того же размера, что и х;

order– порядок конечных разностей (порядок по умолчанию равен 2), доступные значения order: 1, 2 или 4.

Выходные параметры:

J – матрица (необязательный параметр), для функции от одной переменной размером 1х1, для функции от двух переменных – 2х2 (значения частных производных выводятся на ее диагонали);

H– матрица (необязательный параметр), в которую выводятся частные производные второго порядка.

    На рис.2.3.2-1 приведены два варианта вычисления значения производной в точке х=3 от функций, описанных с использованием оператора deff. Причем, в первом примере значение производной вычислено с помощью функции numderivative, а во втором – с использованием выражения производной, полученного заранее в явном виде. Как показали приведенные вычисления, числовые значения производных в точке х=3, полученные двумя способами, полностью совпали.

--> // Вычисление производной от функции f(x) в точке х=3 --> --> deff('[y] = f(x)','y = 2^x – 4 * x'); // Описаниеисходной функции --> --> numderivative(f, 3) // Вычисление производной функции f в точке х=3  ns = 1.5451774 --> --> // Вычисление производной, заданной аналитическим выражением в точке -->deff('[y1] = f1(x)','y1 = 2^x*log(2) - 4'); // Производная функции --> f1(3)                                  // Значение в точкех=3  ans = 1.5451774

Рис. 2.3.2-1. Вычисление производной в точке функцией numderivative

На рис. 2.3.2-2 приведены примеры получения выражений производной от полинома, созданного в аналитическом виде (использование функции derivat)и значения производных в точках x = [1 3 6] (использованиефункции numderivative).

--> // Вычисление производных полинома

-->

-->p = poly([1, 2, 3], "x", "c") // Определение полинома

p =

1 +2x +3x²

-->p1 = derivat(p) // Определение производной от полинома

p1 =

2 +6x

-->ps = pol2str(p) // Преобразование полиноминальное представление
-->// полинома в символьную строку функцией pol 2 str

-->

ps =

1+2*x+3*x^2

-->

-->deff('[sd] = fd(x)', 's = 1 + 2 * x + 3 * x^2') // Описаниефункции fd

--> x = [1 3 6];

--> numderivative(fd, x)

 ans =

8. 0. 0.

0. 20. 0.

0. 0. 38.

-->

-->deff('sp = fp(x)', 'sp='+ ps) // Описание функции fp с использованием sp

--> numderivative(fp, x)

 ans =

8. 0. 0.

0. 20. 0.

0. 0. 38.

Рис. 2.3.2-2. Вычисление производных от полинома

Функция numderivativeпозволяет вычислить и значения частных производных. На рис. 2.3.2-3приведен пример вычисления частных производных от функции трех переменных f ( x ₁ , x ₂ , x ₃ )= x ₁ ² x ₂ + x ₂ ² x ₃ + x ₃ ² x ₁ при х₁=1, x ₂ =3 и х₃=6.

--> // Вычисление частных производных функции трех переменных --> --> deff('s = f(x)', 's = x(1)^2*x(2) + x(2)^2*x(3) + x(3)^2*x(1)') --> -->x = [1 3 6];    // Вектор значений переменных -->numderivative(f, x, 2) // Вычисление второй производной ans = 42. 37. 21.

Рис.2.3.2-3. Вычисление значений частных производных от функции трех переменных с использованием функции numderivative

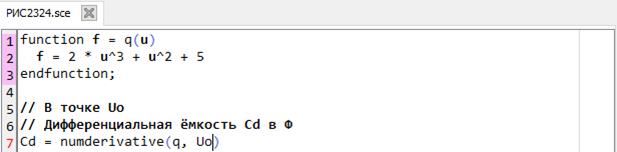
    Вычислить дифференциальную ёмкость нелинейного элемента с ВАХ:
q=2u³+u²+5 в точке U₀=1 В. Решение приведено на рис. 2.3.2-4.

-->// Вычисление дифференциальной ёмкости Cd ВАХ нелинейного элемента -->Uo = 1; --> // Загрузка и выполнение сценария РИС2324 --> exec('РИС2324.sce', 0) --> mprintf('Cd = %g ' ,Cd);  Cd = 8

Рис.2.3.2-4. Вычисление дифференциальной ёмкости нелинейного элемента

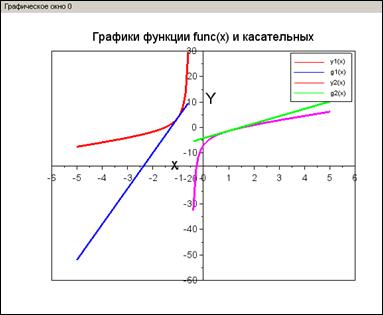
    Построить касательную к функцииf ( x )= ( 3*x²-7 ) / ( 2*x+1 ) (рис. 2.3.2-4).

Рис.2.3.2-5. Построение уравнения и графика производной функции