Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

С помощью функции derivate можно найти рациональную матричную производную от полиномиальной или рациональной матрицы. Функция derivat имеет следующий формат:

   dp = derivat(p),

 

где: p – полиномиальная или рациональная матрица;

dp – рациональная матричная производная.

 

Функция derivat работает с такими выражениями, как 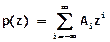, состоит из линейных комбинаций функций с целочисленными показателями одной независимой переменной и реализует аналитическое вычисление .

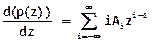       Рассмотрим несколько примеров (рис.2.1.2-2):

 

--> // Вычисление рациональной матричной производной

-->

-->s = poly(0, 's'); // Создание переменной типа полином

-->derivat(1/s) // Вычисляетсяпроизводная(1/ S )'=-1/ s ^2

ans =

-1  

--- 

s²

-->

--> p1 = poly([1 -2 1], 'x', 'c')

 p1 =

1 -2x +x²

-->

--> derivat(p1)

 ans =

-2 +2x

-->

--> p3 = poly(ones(1, 10), 'z', 'c')

 p3 =

1 +z +z² +z³ +z⁴ +z⁵ +z⁶ +z⁷ + z⁸ +z⁹

--> derivat(p3)

 ans =

1 +2z +3z² +4z³ +5z⁴ +6z⁵ +7z⁶ +8z⁷ +9z⁸

 

Рис.2.1.2-2. Вычисление рациональной матричной производной

 

Scilab может выполнять операции над полиномами только с одной переменной, иначе в результате выполнения появляется сообщение об ошибке:

 

«Переменные не имеют одной и той же формальной переменной».

 

В Scilab имеется множество вспомогательных функций по работе с полиномами [14], в том числе, для создания специальных полиномов. В качестве примера рассмотрим создание полинома Чебышева с использованием функции ch epol (рис.2.1.2-3), имеющей следующий формат:

 

Tn=chepol(Порядок полинома , ' Независимая переменная '),

 

где: Tn– полиноминальная переменная, которая в результате присваивания ей результата выполнения функции chepol представляет собой полином
Чебышева.

 

 

-->// Использование функции chepol для создания полинома Чебышев а --> --> T4 = chepol(4, 'x') // Создание полинома Чебышева 4-го порядка Th = 1 -8x2 +8x4 --> --> // Использование функции в выражениях -->P = 2 * poly(0, 'x') * chepol(4,'x') - chepol(5, 'x')  P = -3x +4x3

 

Рис. 2.1.2-3. Использование chepolдля создания полинома Чебышева

 

Далее приведен пример использования вспомогательной функции pol 2 st r, которая преобразует полином в символьную строку (рис. 2.1.2-4).

           

-->// П реобразование полинома в символьную строку

-->

-->p = poly([1, 2, 3], "t", "c")

p =

1 +2t +3t²    // Значение данных типа полином

-->pol2str(p)

ans =

1+2*t+3*t^2 // Значение данных типа строка

 

Рис. 2.1.2-4. Пример преобразования полинома в символьную строку

 

 

Рациональные дроби

Рациональная дробь – объект Scilab r, который является частным двух полиномов r = num / den[13]. Внутреннее представление рациональной дроби это список r = rlist ( num , den ,[] ) или то же самое, что r = num / den. Матрица рациональных чисел может быть определена обычным синтаксисом, например, [ r 11, r 12; r 21, r 22] является матрицей размером 2×2, где rij – рациональные числа размерностью 1 x 1. Матрица рациональных чисел может быть, также определена в виде списка,

 

tlist(['r','num','den','dt'],num,den,[]),

 

где: num и den – матрицы полиномов.

 

Рассмотрим несколько примеров использования рациональных дробей (рис. 2.1.2-5).

 

--> // Представление и работа с рациональными дробями

-->

--> s = poly(0, 's')

 s =

s

--> W = [1/s, 1/(s+1)]

 W =

1 1    

-- ------ 

s 1 + s

-->

--> W' * W

 ans =

1 1         

-- ------      

s² s + s²

1    1       

------ ----------- 

s + s² 1 + 2s + s²

-->

--> Num = [s, s+2; 1, s]

 Num =

s 2 +s

1 s  

--> Den = [s*s, s; s, s*s]

 Den =

s² s

s s²

-->

--> H = Num ./ Den

 H =

1 2 + s  

-- ------ 

s s

 

1 1      

-- --     

s s

-->

--> syslin('c', Num, Den)     //Определениелинейнойсистемы

 ans =

s 2 + s  

-- ------ 

s² s

 

1 s      

-- --     

s s²

 

--> [Num1, Den1] = simp(Num, Den) // Р ациональное упрощение

Den1 =

s s

s s

 Num1 =

1 2 + s

1 1  

 

Рис. 2.1.2-4. Работа с рациональными дробями

 

Полиномы, как с действительными, так и с комплексными коэффициентами, широко используются в теории электрических цепей и теории связи. Например, при анализе нелинейных элементов электрических цепей, для аппроксимации характеристик нелинейных элементов, при расчете переходных процессов в электрических цепях, при синтезе электрических фильтров, при анализе электрических цепей операторным методом, при исследовании цепей на устойчивость. В соответствующих разделах теории электрических цепей также используются полиномы Гурвица, полиномы Батерворта, полиномы Чебышева и другие.

 

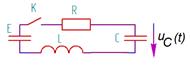
Рассмотрим пример построения временной зависимости напряжения на конденсаторе u_C ( t ) в неразветвленной RLC-цепи, если цепь включается на постоянное напряжение при нулевых начальных условиях [17] (рис. 2.1.2-5).

 

-->//Загрузка и выполнение сценария РИС21205          Колебательный режим	R=0.8; L=0.3e-3; C=0.1e-6;

 

Рис. 2.1.2-5 Построение временной зависимости напряжения на конденсаторе uC(t) в неразветвленной RLC-цепи

 

 

2.1.3 Контрольные вопросы

 

1) Что такое полином?

2) Является ли полином типом данных Scilab?

3) Как создать переменную типа полинома по заданному вектору коэффициентов?

4) Как создать переменную типа полином по заданному вектору корней полинома?

5) Как создать полином с использованием системных констант?

6) Какой формат имеет функция poly?

7) Как задать матрицу полиномов?

8) Как оценить значение полинома?

9) Как вычислить значения корней полинома?

10) Можно ли с полиномами осуществлять операции, такие как: сложение, вычитание, умножение и деление?

11) Как вычислить производную от полинома?

12) Как преобразовать полином в символьную строку?

13) Что представляет собой рациональная матричная производная?

14) Что представляет собой рациональная дробь?

 

2.2. Решения задач аппроксимации и
интерполяции функций

 

2.2.1. Постановка задач аппроксимации
и интерполяции

 

В инженерной и научной работе существенную роль играет решение задачи аппроксимациифункций (подгонка кривых), поскольку зачастую реальные функциональные зависимости слишком сложны для использования или, например, их значения получены в ходе некоторого эксперимента. Задача аппроксимации и состоит в замене исходной функции другой, более простой аналитической функцией, обеспечивающей на некотором множестве точек необходимое приближение, по заданному критерию, ее значений со значениями исходной функции.

В частном случае, когда аппроксимирующая функция во всех узловых точках обеспечивает полное совпадение с аппроксимируемой функцией, задачу аппроксимации функции называют интерполяцией. Интерполяционные формулы имеют не только практическое, но и теоретическое значение. Они лежат в основе квадратурных формул численного интегрирования, методов решения дифференциальных и интегральных уравнений и многих других численных методов. Все перечисленные выше аспекты рассмотрены в классических учебниках по численным методам [22, 23].

Постановка задачи аппроксимации состоит в следующем. Пусть функция задана таблично, то есть имеется набор узловых точек x_k, где
k=1,2,…,n и значения функции y(x_k)в этих точках. Требуется заменить ее некоторой приближенной функцией f(x,a₁,a₂,…,a_m), которая кроме аргумента х, зависит еще и от параметров a_s, где s =1,2,…, m. Задача аппроксимации состоит в том, чтобы подобрать такие значения параметров a_s, при которых аппроксимирующая функция f ( x , a ₁ , a ₂ ,…, a_m ) наилучшим образом описывала бы исходную функцию. Как правило, m << n, поэтому добиться того, чтобы функция f ( x , a ₁ , a ₂ ,…, a_m ) давала точные результаты даже в узловых точках, как правило, не удается. Следовательно, должен быть выбран такой критерий близости, который смог бы обеспечить требуемую точность. В зависимости от решаемой задачи на практике используют различные методы и, соответственно, различные критерии близости. Чаще всего для аппроксимации таблично заданной функции используется метод наименьших квадратов, в котором в качестве критерия близости, аппроксимирующей и аппроксимируемой функций, используется неравенство:

 

,

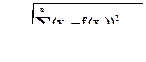где: 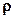 – среднеквадратическое отклонение;

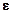 – допустимая погрешность;

у _i– значения аппроксимируемой функции в узловых точках;

f ( x_i ) – значения аппроксимирующей функции в узловых точках;

n +1 – количество узловых точек.

Задача интерполяции функции, как уже отмечалось выше, является частным случаем задачи аппроксимации. Решение задачи интерполяции требует замены таблично заданной функции (y(x_k), где k=1,2,…,n) такой функцией f(x),которая в узловых точках x ₁ , x ₂ ,…, x_nпринимала бы значения заданной функции, то есть другими словами выполнялось бы основное условие интерполяции f ( x_k )= y_k , где k=1,2,…,n. Чаще всего в качестве интерполирующей функции f ( x ) используется полином p ( x ), степень которого n -1 (на единицу меньше количества узлов интерполяции), а интерполяционные формулы [24] в зависимости от метода различаются лишь формами представления полиномов.

При большом количестве базовых точек интерполяция полиномом может оказаться малоэффективной, поэтому нередко используют интерполяцию сплайнами. Идея сплайн-интерполяции [24] состоит в разбиении диапазона интерполирования на отрезки, в пределах которых используются разные функции одного вида (чаще всего алгебраические многочлены). При этом сама функция и ее производные 1-го, 2-го и 3-го порядка во всем диапазоне интерполяции непрерывны. Существуют линейные и квадратичные сплайны, однако, наиболее распространенный и точный вариант интерполяции – интерполяция кубическими сплайнами, в результате которой мы имеем кусочно-непрерывную интерполяционную зависимость.

Очевидно, что решение задач и аппроксимации, и интерполяции функций являются крайне трудоемкими. Это связано с тем, что их точность во многом зависит от количества используемых узловых точек на отрезке и шага интерполяции. Поэтому на практике эти задачи чаще всего решаются с использованием средств математических пакетов [25, 26].

Цель данного раздела – продемонстрировать возможности системы Scilab для изучения базовых вопросов, возникающих при решении задач аппроксимации и интерполяции функций при помощи полиномов. Именно поэтому изложение материала второй части данного учебника мы начали с представления в системах Scilabполиномов и возможных операций над ними.