Задача одномерной оптимизации имеет единственное решение, если функция f ( x ) на отрезке [ a ; b ] имеет только один экстремум, то есть она
унимодальна. Для того чтобы функция на отрезке [ a ; b ] была унимодальной должны выполняться следующие условия [24]:

· Необходимым условием существования экстремума дифференцируемой одномерной функции f ( x ) является выполнение равенства
f ¢ (х) = 0;

· Достаточным условием существования единственного минимума одномерной функции f ( x ) на отрезке [ a ; b ] является возможность дважды ее дифференцировать и требование положительности второй производной f ¢¢ (х) в любой точке этого отрезка.

Задача многомерной оптимизации сводится к нахождению оптимального значения функции n переменных f (Х)= f ( x ₁ , x ₂ ,…, x_n ), определенной в n-мерном пространстве 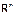, где из множества допустимых решений выбирается такой вектор Х*, которому соответствует минимальное значение целевой функции f (Х*)=_min f (Х).

Для всякой непрерывно дифференцируемой функции f (Х) достаточным условием того, что функция имеет точку минимума, является положительная определенность матрицы вторых частных производных (матрицы Гессе или Гессиан):

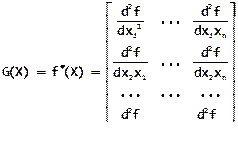
Известно, что матрица положительно определена в том случае, если все её угловые миноры положительны. Так, например, для функции двух переменных f ( x , y ) матрица Гессе имеет следующий вид:

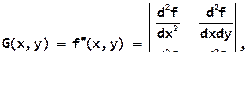
и тогда достаточным условием существования минимума функции f ( x , y ) является выполнение неравенств:

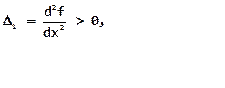
Для решения задачи многомерной оптимизации требуется ввести понятие вектора-градиента функции f (Х):

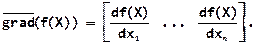
Этот вектор направлен в сторону наискорейшего возрастания функции, но поскольку все методы оптимизации предназначены для поиска минимума, то направление поиска минимума (спуска) противоположно, то есть совпадает с направлением вектора антиградиента: .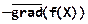

Таким образом, решение задачи многомерной оптимизации является задачей поиска:

· локального оптимума функции – где точка 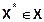является точкой локального минимума функции f (Х) на множестве X, если существует такая d – окрестность U _d этой точки (d >0), что для всех
Х Î Х _d =Х U _d выполняется неравенство f(X*) £ f(X);

· глобального оптимума функции – где точка 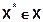является точкой глобального минимума функции f (Х) на множествеX, если функция достигает в этой точке своего наименьшего значения:
f ( X ^* )≤ f (Х), .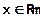

Также известно, что аналитические методы поиска оптимума применимы только для ограниченного круга задач. В основном это связано с тем, что при использовании аналитических методов возникает необходимость вычисления производных и решения нелинейных уравнений (а для многомерных функций – систем нелинейных уравнений), которые тоже, как правило, решаются только численными методами.

Для поиска оптимального значения целевой функции численными методами кроме самой целевой функции необходимо задать точность искомого оптимума Ɛи начальную точку поиска X ₀.

Выбор начального приближения является нетривиальной задачей. Поэтому прежде, чем приступить к численному решению задачи оптимизации нелинейных функций, необходимо провести исследование целевой функции.