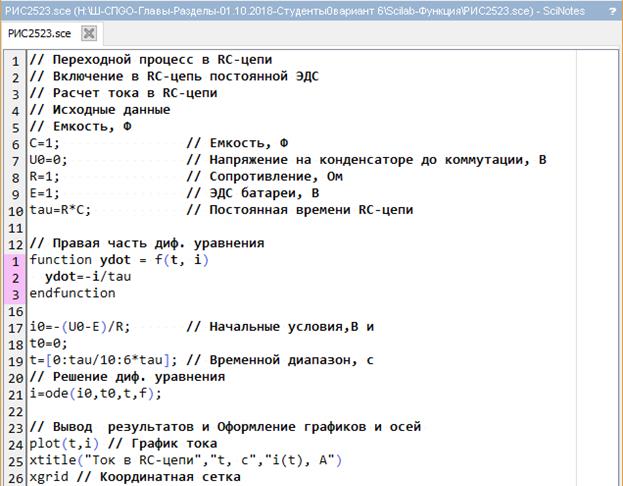
Для решения ОДУ и системы ОДУ 1-го порядка в Scilab предусмотрена функция ode , имеющая форматы:

[y]=ode(y0,t0,t,f),

[y,w,iw]=ode(type,y0,t0,f,adams,stiff,rk,rkf,fix,rtol,adol,jac,w,iw),

которые содержат обязательные и необязательные параметры.

Первый формат функцииode содержит только обязательные параметры, к которым относятся:

y 0 – вектор начальных условий;

t 0 – начальная точка интервала интегрирования;

t – координаты узлов сетки, в которых происходит поиск решения;

f– имя внешней функция, определяющей правую часть уравнения

или системы уравнений;

y – вектор решений (выходной параметр).

Второй формат функции odeсодержит ряд необязательных параметров. Эти параметры позволяют выбрать метод решения или тип решаемой задачи:

type– строка, указывающая тип используемой программы решения, может принимать значения: " adams ", " stiff ", " rk ", " rkf ", " fix ", " discrete "или " root ";

adams– применяют при решении дифференциальных уравнений или систем методом прогноза и коррекции Адамса;

stiff– указывают при решении жестких задач;

rk– используют при решении дифференциальных уравнений или систем методом Рунге-Кутты четвертого порядка;

rkf– указывают при выборе пятиэтапного метода Рунге-Кутты четвертого порядка;

fix– тот же метод Рунге-Кутты, но с фиксированным шагом;

rtol, atoll– относительная и абсолютная погрешности вычислений, соответственно, по умолчанию rtol =0.00001, atol =0.0000001 (при использовании параметров rkfи fix– rtol =0.001, atol =0.0001);

jac– матрица, представляющая собой якобиан правой части жесткой системы дифференциальных уравнений и заданная в виде внешней функции вида j = jak ( t , y );

w, iw– векторы, предназначенные для сохранения информации о параметрах интегрирования, которые применяют для того, чтобы последующие вычисления выполнялись с теми же параметрами.

Описание этого формата достаточно подробно рассмотрено в справочной системе Scilab, где и приведены примеры его использования для различных типов ОДУ [13].

Остановимся на использовании первого формата функции ode, для чего рассмотрим решение следующего примера: найти решение ОДУ y '=- sin ( x * y ) на отрезке [0;5]cшагом 0.5 при начальных условиях y (0)=1.5.

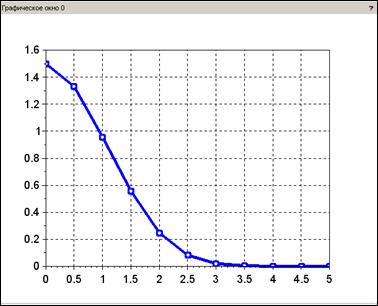
Решение ОДУ, полученное с применением функции ode и график полученного решения, представлены на рис.2.5.2-1.

--> // Решение ОДУy'=-sin(x*y) --> y0 = 1.5; t0 = 0; t = 0:0.5:5; // Начальные условия --> // Загрузка и выполнение сценарияРИС2521 --> exec('РИС2521.sce', 0);    ans = 0. 1.5      0.5 1.3302706 1. 0.9566472 1.5 0.5574285 2. 0.2477507 2.5 0.0822207 3. 0.0208664 3.5 0.0041103 4. 0.0006303 4.5 0.0000753 5. 0.000007

Рис. 2.5.2-1. Решение ОДУ с использованием функции ode

Для решения системы обыкновенных дифференциальных уравнений в Scilab предназначена функция:

y=ode(x0,t0,t,sys),

где х0 – вектор начальных условий ОДУ;

t 0 – начальная точка интегрирования;

t– вектор значений независимой переменной;

sys– имя функции, в которой исходя из вектора значенийtвычисляется матрица решенийy;

y– матрица решений (выходной параметр), первый столбец которой

y (1)– значение функции y ( x ), а второй - y (2 )–значение производной y '( x ).

 Решение системы ОДУ формируется в матрице y, и выводится на экран в виде таблицы

В качестве примера рассмотрим решение системы ОДУ:

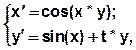
c начальными условиями x(0)=0, y (0)=0 на отрезке [ 0;10] и шагом 1 .

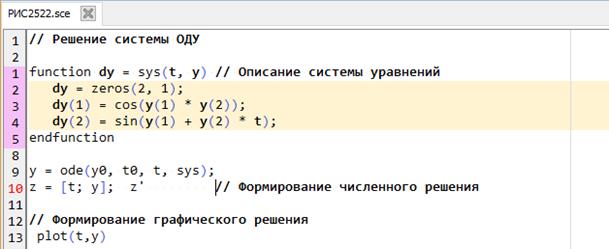
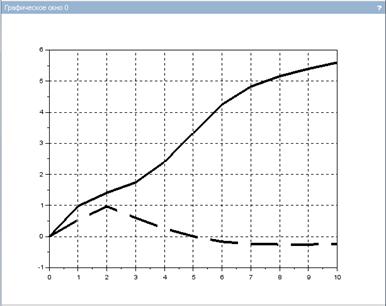
Решение системы ОДУ в Scilab начинается с создания функции sys, описывающей систему (рис.2.5.2-2). После того, как заданы начальные условия ОДУ, производится обращение в функции ode, в результате которого формируется матрица решения y. Решение системы выводится в виде таблицы и графика. (Шапка таблицы и легенда для графика!)

--> // Решение системы ОДУ --> // Загрузка сценария РИС2522 и его выполнение -->clear --> // Начальные условия -->x0 = [0; 0]; t0 = 0; t = 0:1:10; --> --> exec('РИС2522.sce', 0);  ans = 0. 0.     0.       1. 0.9802401 0.533358 2. 1.4096497 0.9693978 3. 1.7429464 0.6024417 4. 2.4027415 0.2586293 5. 3.3312751 0.005761 6. 4.2504071 -0.1650347 7. 4.826261 -0.2358589 8. 5.1581587 -0.2515654 9. 5.3963437 -0.2509281 10. 5.5981318 -0.2461951

Рис.2.5.2-2. Решение системы ОДУ

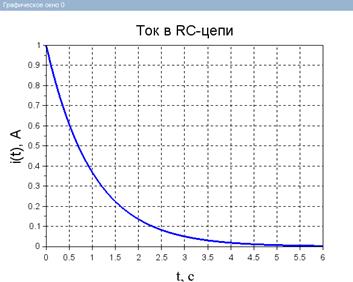
Рассмотрим задачу построения временной зависимости тока i ( t ) в RC-цепи.

Построить временную зависимость тока i ( t ) в неразветвленной RC-цепи (рис. 3.3-4), если цепь включается на постоянное напряжение при нулевых начальных условиях.

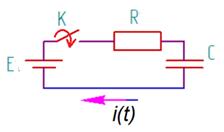	Неразветвленная RC -цепь Дано: E=1 В – ЭДС источника; R=1 Ом – сопротивление; С=1 Ф – емкость; t=[0, 6τ] c – временной интервал.

Рис.2.5.2-3. Построить временную зависимость тока i ( t ) в RC-цепи