В простейшем случае полиномы – это выражения от одной независимой переменной, например, x с неотрицательными целыми показателями степени:

P(x)=a₀+a₁x+a₂x²+…+a_nxⁿ,

где a_i– коэффициенты при неизвестных ( i =0,1,…, n ) .

В Scilab полином такого вида является одним из типов данных (п. 1.2). Для создания полинома необходимо сначала сформировать вектор-строку, содержащий значения коэффициентов при неизвестных, упорядоченных по восходящим степеням. В общем виде полином n -й степени можно описать вектор-строкой vPn =[ a 0, a 1, a 2,…, an ], а его решение, то есть корни полинома, представить в виде вектора vXn =[ x 0, x 1, x 2,…, xn ].

Так, например, полином 2-й степени Р₂ ( x )=6-5 x + x ² в Scilabможно представить вектором vP 2=[6 -5 1], а его корни – [2 3].

При этом члены полинома, которые имеют нулевые коэффициенты, обязательно должны быть представлены в векторе vP2нулем. Ноль действует в векторе как заполнитель для той особой степени x, которая отсутствует в математической записи полинома. Так, например, для представления многочлена P ₅ ( x )=21+2 x -3 x ² +4 x ⁵, вектор коэффициентов, представляющий этот полином, должен иметь вид: vP5=[21 2 -3 0 0 4].

Другим простейшим способом создания полинома является использование системных констант %z и % s, описанной в п.1.2.1, имеющих полиномиальный тип (рис. 2.1.1-1).

--> // Создание переменной t типа полином

-->t = 1 + 5*%z

t =

1 +5z

Рис. 2.1.1-1. Использование системной константы %z для создания полинома

В Scilab имеется специальная функция poly [13], предназначенная для представления полинома (переменной полиномиального типа). Эта функция имеет два принципиально разных формата.

Первый формат poly создает переменную типа полинома по заданному вектору коэффициентов:

Р= poly (ВекторКоэфициентовПолинома, 'ПеременнаяПолинома', 'с'),

где: ВекторКоэфициентовПолинома – вектор коэффициентов полинома (vP);

с – признак формата, заключенный в одинарные кавычки, означающий, что должен быть сформирован полином с коэффициентами, хранящимися в параметре ВекторКоэфициентовПолинома;

Р – переменная, которая после присваивания ей результата выполнения функции poly, представляет собой полином и приобретает полиномиальный тип (polynomial) (п. 1.2.1).

Второй формат функции poly предназначен для создания переменной типа полином по заданному вектору корней полинома:

P= poly (ВекторКорнейПолиномов, ‘ПеременнаяПолинома', ' r'),

где: ВекторКорнейПолиномов – вектор корней полиномов (vХ);

r – признак формата, означающий, что значения параметра ВекторКорнейПолиномов воспринимаются функцией как корни, для которых необходимо рассчитать коэффициенты соответствующего полинома, если признак формата не задан, по умолчанию предполагается r.

Использование различных значений параметра формата (c и r) показано в примере, приведенном на рис. 2.1.1-2.

--> // Примеры и спользования функции poly для создания полиномов

-->

--> P1 = poly([2 3], 'x', 'r') 

 P1 =

6 -5x +x²

-->

--> P2 = poly([1 2 3], 'x', 'c')

 P2 =

1 +2x +3x²

-->

--> vP5 = [21 2 -3 0 0 4]

 vP5 =

21. 2. -3. 0. 0. 4.

--> P3 = poly(vP5, 't', 'c')

 P3 =

21 +2t -3t² +4t⁵

-->

--> vK5 = [21 2 -3 0 0 4]

 vK5 =

21. 2. -3. 0. 0. 4.

--> P4 = poly(vK5, 'y', 'r')

 P4 =

-504y² +234y³ +53y⁴ -24y⁵ +y⁶

Рис. 2.1.1-2. Примеры применение функции poly

--> // Примеры создания матриц полиномов --> -->vD = [1 %z, 2 +2*%z, 3 -5*%z] vD = 1 z 2 +2z 3 -5z --> -->mD = [1 +%z, 2 -2*%z; 3 +3*%z, 4 -4*%z] mD = 1 +z 2 -2z 3 +3z 4 -4z --> --> y = %z  y = z --> -->s = poly(0, 'x') // или( s = % z ) Создание полиномиальной переменной s -->p = 1 –2*s +5.2*s^2; // Выражение для формирования элемента матрицы -->M =[p, p-1, p-1.2]  // Создание матрицы-строки M = 1 -2x +5.2x2, -2x +5.2x2, -0.2 -2x +5.2x2 --> -->v = [p; p+1; p-p^2] // Создание матрицы-столбца V = 1 -2x +5.2x2 2 -2x +5.2x2 2x -9.2x +20.8x3 -27.04x4 --> -->C = [p, p/2; p+1, p*2; p, p+2] // Создание матрицы С(3 x2) C = 1 -2x +5.2x2 0.5 -x +2.6x2 2 -2x +5.2x2 2 -4x +10.4x2 1 -2x +5.2x2 3 -2x +5.2x2 --> s = poly (0, ' x ');        //Создание переменной типа полинома --> // Полиномы для формирования элементов матрицы -->c11 = poly([3, 2, 1], 'x', 'c'); --> c12 =poly([4, 0, 1], 'x', 'c'); --> c13 = poly([5.3, -1.01, sin(2)], 'x', 'c'); --> c21 = poly([-3.1, 1.5, log(0.15)], 'x', 'c'); --> c22 = poly([4, 2.5, 0], 'x', 'c'); --> c23 = poly([%e, 2.4, 0.56],'x', 'c'); --> C = [c11, c12, c13; c21, c22, c23]  C = 3 +2x +x2 4 +x25.3 -1.01x +0.9092974x2 -3.1 +1.5x -1.89712x2 4 +2.5x 2.7182818 +2.4x +0.56x2

Рис. 2.1.1-3. Создание матриц полиномов

Чтобы создать полиномиальную матрицу заданного размера и заполнить ее полиноминальными элементами можно, воспользоваться системной переменной % z или создать новую полиноминальную переменную, а затем сформировать матрицу одним из стандартных способов, рассмотренных ранее в п. 1.2.3 (рис. 2.1.1-3).

Чтобы создать полиномиальную матрицу заданного размера и заполнить ее полиноминальными элементами можно, воспользоваться системной переменной % z или создать новую полиноминальную переменную, а затем сформировать матрицу одним из стандартных способов, рассмотренных в
п. 1.2.3 (рис. 2.1.1-3).

Оценка значений полиномов

Для оценки значений полиномов в Scilabиспользуется функция

A=horner (p ,х),

где p– полиномиальная матрица, x– матрица значений переменной полиномов p, а A– значения полиномов pпри заданных значениях x(рис.2.1.1-4).

--> // Оценка значений полиномов с использованием функции horner --> -->// Оценка полинома для заданного значения -->a1 = poly(1:3, 'y') a1 = -6 +11y -6y2 +y3 --> --> horner(a1, 1)  ans = 0. --> --> // Оценка полинома для матрицы значений -->х = [12; 34] х = 12. 34. --> a2 = poly([1 2 3], 'x', 'c')                 a2 = 1 +2x +3x2 --> --> h = horner(a2, х)  h = 457. 3537.

Рис. 2.1.1-4. Оценка значений полиномов с помощью функции horner

Вычисление корней полиномов

Для нахождения корней полинома можно использовать функциюScilab

X=roots(p) ,

где: p – полином с вещественными или комплексными коэффициентами, или вектор вещественных значений m×1 (1×m) полиномиальных коэффициентов в порядке убывания степени; X – вектор корней уравнения.  

    В данном случае используется алгоритм, основанный на собственных значениях сопутствующих матриц [20], и позволяющий за одно обращение к функции roots вычислить все корни заданного полинома (рис. 2.1.1-5).

--> // Нахождение корней полинома функцией roots --> -->a = [-1 0 8 -8 2]; // Коэффициенты полинома -->p = poly(a, 'x', 'c') // Определение полинома p = -1 +8x2 -8x3 +2x4 --> -->X = roots(p) // Нахождение корней полинома по заданному полиному p X = 2.306563  1.5411961  -0.306563  0.4588039 --> --> da = size(a, "*")  da = 5. -->y = roots(a(da:-1:1)) // Нахождение корней полинома y = 2.306563  1.5411961  -0.306563  0.4588039 --> -->isreal(y) // Проверка: являются ли корни действительными? Нет ans = F -->y = real(y) // Преобразование из мнимых значений в действительные y = 2.306563 1.5411961 -0.306563 0.4588039 --> -->isreal(y) // Проверка: являются ли корни действительными? Да ans = T

Рис. 2.1.1-5. Нахождение корней полинома функцией roots

Обратите внимание, что при вычислении корней полинома (функция roots ) вектор коэффициенты полинома должен быть представлен в порядке убывания степени, в то время как при определении полинома (функция poly ) вектор коэффициенты полинома должен быть представлен в порядке возрастания степени.

Предполагается, что функция roots всегда возвращает корни полинома как комплексные числа, даже если мнимая часть равна нулю. Конвертировать их в действительные значения можно с помощью функции real,а для проверки типа полученных корней можно использовать функцию isreal.

Рассмотрим пример из ТЭЦ, который позволяет проверить, является ли устойчивой электрическая цепь с передаточной функцией вида:
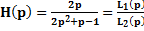[17] (рис. 2.1.1-6).

--> // Загрузка и выполнение сценария РИС21106 --> -->Vk = [-1 1 2];     // Задание коэффициентов полинома -->exec('РИС21106.sce', 0) Pk1 = 0.5 Pk2 = -1 --> //КореньPk1 оказался в правой полуплоскости, --> //следовательно, цепь неустойчива

Рис. 2.1.1-6. Проверка устойчивости электрической цепи