Исследование целевой функции можно осуществлять как графически, так и аналитически.

Проведение графического исследования поведения целевой функции (которое возможно только для функций от одной и двух переменных) очень полезно с точки зрения того, что можно не только визуально удостовериться в наличии оптимума, но и провести правильный выбор начальной точки его поиска.

Так в случае одномерной оптимизации можно в области допустимых значений xпостроить график целевой функции, например,

f ( x )= x ⁴ + 3 x ³ - 13 x ² - 26 x + 26,

который позволяет определить отрезок, содержащий единственный минимум, а затем на этом отрезке, выбрать точку, которая будет использована в качестве начального приближения для дальнейшего уточнения координат точки минимума с требуемой точностью (рис.2.7.1-2).

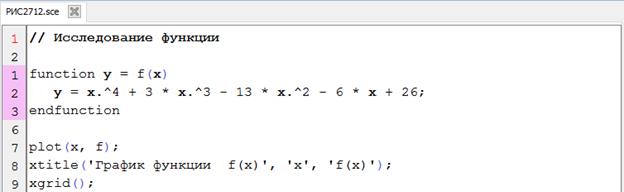
--> // Исследование функции на интервале (-100; 100) --> -->scf(0) -->x = -100:0.1:100; --> // Загрузка сценария РИС2712 --> exec('РИС2712.sce', 0)

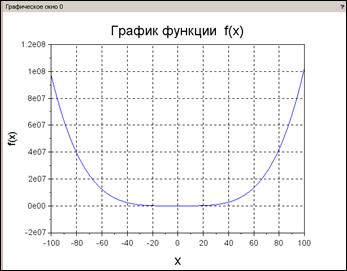
--> // Уточнение границ отрезка на интервале (-5; 1) --> -->scf(1) --> x = -5:0.1:1; --> exec('РИС2712.sce')

Рис. 2.7.1-2. Исследование графика целевой функции f(x)

Из графика следует, что на отрезке [-4.5;-3] имеется один локальный минимум. После графического исследования, если это возможно, полезно провести аналитическое исследование функции: вычислить первую и вторую производные целевой функции, и убедиться, что на отрезке [-4;-3] f ¢ (х) меняет знак с минуса на плюс, а f ¢¢ (х) –положительна.  

Полученная таблица значений функции и производных (2.7.1-3) подтверждает правильность выбора отрезка [-4;-3], следовательно, из этого отрезка и будет выбрана начальная точка для дальнейшего уточнения точки минимума.

--> // Аналитическое исследование функции f(x) на отрезке [-4; -2] --> --> // Загрузка сценария РИС2713 -->exec('РИС2713.sce', 0) --> x = -4 : 0.5 : -3; y = f(x); y1 = f1(x); y2 = f2(x); --> // Таблица значений функции и двух ее производных --> disp([x; y; y1; y2]',[' x ', ' y ', ' y1 ', ' y2 ']);    ! x y    y1 y2 ! -4. 22500. -14. 94. -3.5 12656.25 23.75 58. -3. 6400. 45. 28.

Рис. 2.7.1-3. Аналитическое исследование функции f(x) на отрезке [-4;-3]

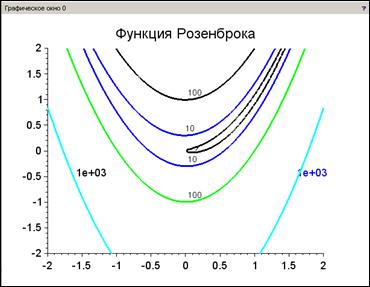
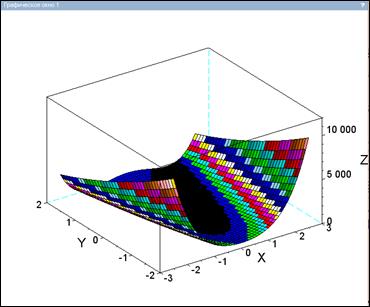
Проведем исследование поведения функции от двух переменных. Например, предположим, что необходимо выбрать начальную точку для поиска минимума функции Розенброка:

f ( x ₁ , x ₂ )=100(x₂-x₁ ² ) ² +(1- x ₁ ) ².

Отметим, что функция Розенброка является тестовой функцией для многих методов оптимизации в связи с тем, что она относится к классу овражных функций, для которых результат поиска сильно зависит от выбора начальных условий.

Построим график поверхности и контурное изображение функции, которые помогут визуально оценить оптимальную область функции
Розенброка (рис. 2.7.1-4).

-->// Исследование функции rosenbrock --> -->exec('РИС2714.sce', 0);  --> xdata = linspace(-2, 2, 100); --> ydata = linspace(-2, 2, 100); --> contour(xdata, ydata, rosenbrock, [1 10 100 1000]) --> [x, y] = meshgrid(-2:0.1:2, -2:0.1:2); --> z = rosenbrock(x, y); --> scf(1); surf(x, y, z);

Рис. 2.7.1-4. Исследование функции Розенброка f ( x ₁ , x ₂ )

Из контурного графика функции следует, что минимальным является контур со значением функции f=1. Следовательно, в качестве начальной точки поиска минимума может быть выбрана, например, точка с координатами (0,0), определяемая в Scilab вектором x=[0,0].

Построение контурного графика может послужить первым шагом для нахождения оптимального решения многомерной функции, и, кроме того, позволяет сократить количество итераций по поиску оптимума. Однако получить графическое изображение функции можно только тогда, когда у нас есть ограниченное количество входных переменных (1 или 2). Во всех остальных случаях приходится сразу приступать к использованию численных алгоритмов и тогда начальное приближение выбирается исходя из пространства допустимых значений конкретной функции.

2.7.2. Численные методы оптимизации и их
реализация в Scilab