Если функция задана таблично, то для вычисления значения производной в точке, необходимо предварительно получить значения конечных разностей, поскольку в основе численного дифференцирования, как уже отмечалось выше, лежит аппроксимация функции, от которой берется производная, заменяемая интерполяционным многочленом Ньютона

.

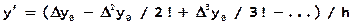Именно поэтому численное дифференцирование еще называют аппроксимированным дифференцированием.

Для получения конечных разностей, входящих в состав интерполяционного многочлена, в Scilab используется функция diff, которая может иметь один из следующих форматов:

dy=diff(y);

dy=diff(y,n);

dy=diff(y,n,dim),

где y– вектор или матрица (вещественная, комплексная или полиномиальная) табличных значений функции;

n – порядок конечных разностей (целое число), по умолчанию значение n равно 1;

dim – размерность матрицы, по которой происходит вычисление конечных разностей. Размерность может принимать значения как 'r', 'c' или 1, 2 соответственно (по строкам или столбцам), так и'*' (по всем элементам матицы). По умолчанию значение dim равно "*", то есть запись diff( y , n ) равносильна записи diff( y , n , '*' ).Если параметр dim имеет значение 'r', то это эквивалентно записи dim=1, а dim='c' – эквивалентно dim=2 .

dy – скаляр или матрица значений конечных разностей.

Формат dy=diff(y) предназначен для вычисления разностей между соседними значениями y (y(2:$)-y(1:$-1)), поскольку по умолчанию n=1. При использовании формата dy=diff( y , n ) функция diff вычисляет n-конечные разности, а использование формата dy=diff( y , n , dim ) позволяет вычислить n-ые разности при заданной размерности dim.

На рис.2.3.2-4 приведен пример вычисления значений производной от функции y(x)=log10(x), заданной в виде таблицы. Зная аналитическое выражение для производной от функции y(x ) (y'=1/ln(10)/x), в примере проведена проверка результата, полученного при использовании функции diff.

--> // Вычисление значений производных для функции, заданной таблично --> --> x = 10 : 5 : 25; h = 5; --> y = log10(x); // Дифференцируемая функция --> --> // Конечные разности 1-го, 2-го и 3-го порядка --> dy = diff(y); dy2 = diff(y, 2); dy3 = diff(y, 3); --> --> // Приближенные значенияy'(x) в точкахx = 10, 15, 20 --> y10 = (dy(1) - dy2(1)/2 + dy(1)/3) / h  y10 = 0.0520729 --> Y15 = (dy(2) - dy2(2)/2) / h  Y15 = 0.0277906 -->Y20 = dy(3) / h Y20 = 0.019382 --> --> // Значения производных функции log10(x) --> (1/log(10)) ./ x(1:$-1) ans = 0.0434294 0.028953 0.0217147

Рис. 2.3.2-4. Вычисление производных по таблице значений функции

На рис. 2.3.2-5 показана еще одна возможность приближенного вычисления производных функции y = sin ( x ), заданной таблично. Принимая во внимание, что для исходной функции известно аналитическое выражение производной (y'= cos ( x )), с помощью функции norm (норма матрицы), можно получить значение максимального отклонения приближенных значений производных от их соответствующих точных значений, полученных по аналитической формуле.

--> // Аппроксимированное дифференцирование --> x = 1 : 0.01 : 1.05; h = 0.01; --> // Функция, от которой берется производная --> y = sin(x); --> // Аппроксимированное вычисление производной функции --> dy = diff(sin(x) ./ h) dy = 0.536086 0.5276177 0.5190967 0.5105238 --> y1 = cos(x) // Производная от функции sin ( x )  y1 = 0.5403023 0.5318607 0.523366 0.5148188 0.5062203 --> // Максимальный элемент вектора модулей разностей --> norm(dy - cos(x(1:$ - 1)), %inf)  ans = 0.0043204

Рис. 2.3.2- 5. Аппроксимированное дифференцирование

Поскольку результат выполнения функции norm ( V ,% inf ) равен значению максимального элемента вектора Vпо модулю, то в данном он равен значению 0.0043204.

2.3.3. Постановка задачи численного
интегрирования

Интегрирование – это распространенная математическая операция для решения многих задач науки и техники. С его помощью проводят вычисление площадей, скорости, ускорения, перемещения и многое другое. Интегрирование простых функций можно легко провести аналитически, но чем сложнее подынтегральная функция, тем труднее, а иногда невозможно, получить точное значение интеграла. Следует также отметить, что, если в курсах математического анализа подынтегральная функция обычно задана аналитически, то в прикладных задачах она может быть задана в виде таблицы, поскольку здесь часто используются данные экспериментов.

Определенный интеграл в общем виде имеет вид:

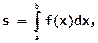
где: f ( x )– подынтегральная функция;

а и b – пределы интегрирования.

Исходя из геометрической интерпретации, значение интеграла s численно равна площади области, ограниченной графиком функции, осью абсцисссО X и двумя прямымиx=а и x=b. При численном интегрировании эта область разбивается на несколько частей, вычисляется площадь каждой маленькой части, а затем они суммируются. Существует множество численных методов, которые отличаются способами разбиения области интегрирования на части и способами вычисления площади каждой из этих частей [22].

Суть всех формул численного интегрирования состоит в том, что на элементарных отрезках интегрирования подынтегральную функцию заменяют простейшим интерполяционным полиномом, который легко может быть проинтегрирован в аналитическом виде. Так, например, для получения формул прямоугольников, трапеций и Симпсона используют полиномы соответственно нулевой, первой и второй степени.

2.3.4. Численное вычисление определенных
интегралов средствами Scilab