В современном машиностроении наиболее распространённым типом механических передач являются зубчатые передачи. Это передачи зацеплением при помощи непосредственного контакта звеньев. Ведущее звено передачи называется шестерня, ведомое звено - зубчатое колесо. В большинстве случаев зубчатая передача служит для передачи вращательного движения, но встречается её использование и как механизма для преобразования вращательного движения в поступательное (передача шестерня – рейка).

Классификация зубчатых передач.

Зубчатые передачи и зубчатые колёса классифицируют по следующим признакам:

1. По взаимному расположению осей валов, на которые одеваются зубчатые колёса:

1.1. Цилиндрические – оси параллельны (рисунок 33 а, б, в, д).

1.2. Конические – оси пересекаются (рисунок 33 з, и).

1.3. Винтовые – оси перекрещиваются (рисунок 33 е).

1.4. Шестерня – рейка – для преобразования вращательного движения в поступательное и наоборот (рисунок 33 г ).

1.5. Гипоидная (рисунок 33 к ).

2. По виду зацепления в зависимости от взаимного расположения шестерни и зубчатого колеса внутреннее зацепление (рисунок 33 е), внешнее зацепление (рисунок 33 все остальные).

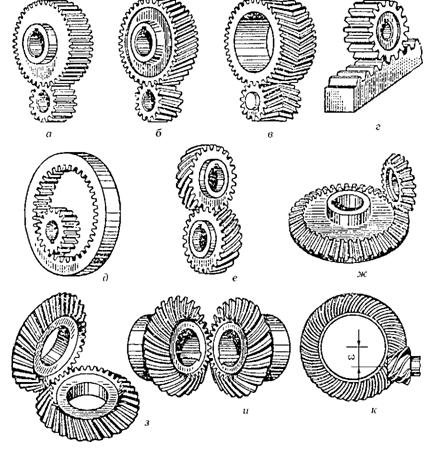
Рисунок 33. Виды зубчатых передач.

3.  По расположению зубьев относительно образующей колёс:

3.1. Прямозубые (рисунок 33 а, ж).

3.2. Косозубые (рисунок 33 б, з).

3.3. Шевронные (рисунок 33 в).

3.4. С криволинейным зубом (рисунок 33 е, и).

При переходе от прямозубых передач к непрямозубым возрастает плавность работы, уменьшается износ и шум, растёт несущая способность. Ввиду этого непрямозубые передачи могут работать при более высоких скоростях и передавать большие мощности.

4. По профилю боковой поверхности зуба:

4.1.Эвольвентные. Боковые поверхности зубьев очерчены по эвольвенте. Такие передачи получили преимущественное распространение, т.к. эвольвента считается наиболее технологичной кривой.

4.2. С круговым профилем (зацепление Новикова). Боковые поверхности зубьев очерчены по окружности. Такие передачи отличаются повышенной надёжностью. Применяются редко, т.к. их изготовление более затратно.

5. По конструктивному оформлению:

5.1.Закрытые – размещены в специальном непроницаемом корпусе и обеспеченные постоянной смазкой.

5.2. Открытые – работают без смазки или периодически смазываемые.

6. По окружной скорости:

6.1.Тихоходные (v < 3 м/с).

6.2. Среднескоростные (V = 3…15 м/с).

6.3. Быстроходные (v > 15 м/с ).

Цилиндрические прямозубые передачи.

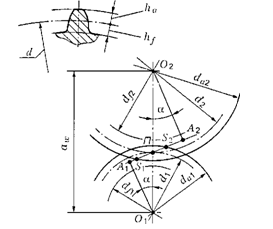
Рисунок 34. Геометрия цилиндрической передачи.

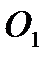
 - линия центров передачи.

П -  полюс зацепления – точка на линии центров, в которой соприкасаются зубья.

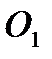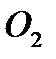Окружности с центрами в  и , соприкасающиеся в полюсе называются начальными окружностями зацепления. Их диаметр обозначают  и .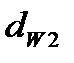

Зацепление считается нормальным, если его начальные окружности совпадают с делительными окружностями колёс.

Делительной окружностью считается та окружность, по которой ширина зуба равна ширине впадины. Делительные окружности обозначают 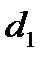 и .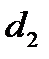

Величина диаметра делительной окружности определяется по формуле:

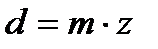
 - число зубьев.

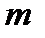 - модуль зубчатого колеса – основная его геометрическая характеристика.

Делительная окружность делит зуб на 2 равные части: верхнюю (меньшую) высотой 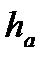 называют головкой зуба и нижнюю (большую) высотой  называют ножкой.

У нормального зацепления высота головки равна модулю, а высота ножки 1,25 модуля.

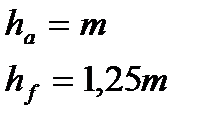
Окружность, ограничивающая выступы называется окружностью выступов. Её диаметр равен:

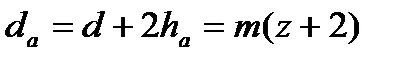
Окружность, ограничивающая впадины называется окружностью впадин. Её диаметр равен: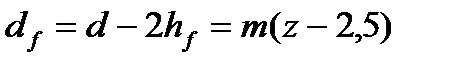

Способы определения модуля :

1) По отпечатку зуба (рисунок 35).. Высота зуба Н = h_a + h_f = m +1,25m = 2,25m   

Следовательно, m =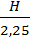

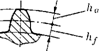
Рисунок 35. Отпечаток зуба.

2) По диаметру выступов:  m =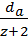

3) По диаметру впадин: m =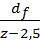

hh – общая нормаль, tt – общая касательная.

𝛼 – угол зацепления (у нормального зацепления 𝛼 = 20^∘).

А₁А₂ – линия зацепления.

S₁ S₂  – длина активной линии зацепления.

Усилия в зацеплении. (рисунок 36).

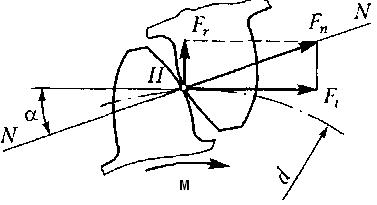
Рисунок 36. Усилия в зацеплении цилиндрических прямозубых колёс.

Зуб шестерни оказывает давление на зуб колеса с силой, которая направлена по общей нормали NN/  Она обозначается .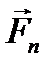

Для удобства расчетов эту силу раскладывают на две составляющие:

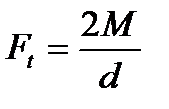 - окружная сила – направлена по общей касательной.

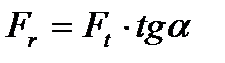 - радиальная сила.