В квантовой физике частица, движущаяся в свободном пространстве, может обладать любой энергией. Ее энергетический спектр – сплошной. У частицы, которая движется в силовом поле, удерживающем ее в ограниченной области пространства, спектр собственных значений энергии оказывается дискретным. Примером может служить финитное (т. е. ограниченное) движение электрона в кулоновском поле ядра атома водорода. Дискретность энергетических уровней частиц, запертых в ограниченной области, вытекает из двойственной природы частиц и является принципиальным отличием квантовой физики от классической.

Простой физической моделью финитного движения может служить движение частицы в одномерной «потенциальной яме» с бесконечно высокими стенками. Частица не может покинуть область размером L. Она движется в этой области, испытывая многократные отражения от стенок. С волновой точки зрения между стенками во встречных направлениях движутся две волны де Бройля. Это напоминает картину двух встречных волн, бегущих по струне с закрепленными концами. Как и в случае струны, стационарным состояниям соответствуют стоячие волны, которые образуются при условии, что на длине L укладывается целое число полуволн:

Таким образом, стационарным состояниям L = n · (λ / 2) (n = 1, 2, 3, ...)

соответствует дискретный набор длин волн. Поскольку в квантово-механическом случае длина волны λ однозначно связана с импульсом частицы: λ = h / p, а импульс частицы определяет энергию ее движения: E = p² / (2m) (нерелятивистское приближение), то квантованной оказывается и энергия частицы. Квантово-механический расчет приводит к следующему выражению: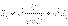

Здесь m – масса частицы, h – постоянная Планка, E₁ = h² / (8mL²) – энергия наинизшего состояния.

Следует обратить внимание, что квантово-механическая частица в отличие от классической не может покоиться на дне потенциальной ямы, то есть иметь энергию E₁ = 0. Это противоречило бы соотношению неопределенностей

Действительно, у покоящейся частицы импульс строго равен нулю, следовательно, Δp_x = 0. В то же время неопределенность координаты частицы Δx ≈ L. Поэтому произведение Δx · Δp_x у частицы, лежащей на дне потенциальной ямы, должно было бы равняться нулю.

Соотношение неопределенностей позволяет сделать оценку минимальной энергии E₁ частицы. Если принять, что в состоянии с минимальной энергией p_x ≈ Δp_x, то для минимальной энергии E₁ получается выражения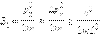

Эта грубая оценка дает правильное по порядку величины значение E₁.

Стоячие волны де Бройля, образующиеся при движении частицы в потенциальной яме, это и есть волновые или пси-функции, с помощью которых квантовая механика описывает стационарные состояния микрообъектов. Квадрат модуля |Ψ|² волновой функции определяется как вероятность нахождения частицы в различных точках пространства.

В компьютерной модели можно изменять ширину L потенциальной ямы, а также массу m запертой в ней частицы. В левом окне высвечиваются графические изображения волновых функций Ψ(x) или квадратов их модулей |Ψ|² для нескольких стационарных состояний (n = 1–5). В правом окне изображается энергетический спектр частицы, то есть спектр возможных значений ее энергии. Обратите внимание, что энергетические уровни опускаются при увеличении ширины L потенциальной ямы и массы m запертой в ней частицы.

В компьютерной модели масса частицы выражается в массах протона m_p = 1,67∙10^–27 кг. Следовательно, моделируются состояния сравнительно тяжелых частиц (ядер тяжелых атомов), оказавшихся в потенциальной яме с шириной порядка размеров атомов.

2) Гармонический осциллятор в квантовой механике представляет собой квантовый аналог простого гармонического осциллятора, при этом рассматривают не силы, действующие на частицу, а гамильтониан, то есть полную энергию гармонического осциллятора, причём потенциальная энергия предполагается квадратично зависящей от координат. Учёт следующих слагаемых в разложении потенциальной энергии по координате ведёт к понятию ангармонического осциллятора.

Модель квантового гармонического осциллятора служит первым приближением для описания колебательного движения в молекулах. Для более точных расчетов (например, при больших амплитудах колебаний) могут быть использованы более точные модели потенциалов, например, потенциал Морзе.

Квантовый гармонический осциллятор — одна из немногих систем в квантовой механике, для которой может быть получено точное решение уравнения Шрёдингера.