Прохождение частицы сквозь барьер можно пояснить соотношением неопределенностей. Неопределенность импульса на отрезке Δx = l составляет Связанная с этим разбросом кинетическая энергия может оказаться достаточной для того, чтобы полная энергия оказалась больше потенциальной и частица может пройти через барьер.

С классической точки зрения прохождение частицы сквозь потенциальный барьер при E < U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является специфическим квантовым эффектом. Основы теории туннельных переходов заложены работами советских ученых Л.И. Мандельштама и М.А. Леонтовича в 1928 г. Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например α-распад, протекание термоядерных реакций).

2) Туннельным эффектом называется прохождение микрочастицы сквозь потенциальный барьер. Потенциальный барьер – увеличение потенциальной энергии в некоторой области пространства. На рис. 12 изображен прямоугольный потенциальный барьер шириной d. Если частица находится в области координат 0 < x < x₁ и имеет полную энергию E (рис. 12), то по законам классической физики она не может преодолеть изображенный на рис. 12 потенциальный барьер, так как в области x₁ < x < x₂ полная энергия меньше потенциальной, следовательно, кинетическая энергия E – E_p < 0, что бессмысленно.

6.КВАНТОВЫЕ ЧИСЛА. Спин электронов. Квантовые числа – целые или дробные числа, определяющие возможные значения физических величин, характеризующих квантовую систему (молекулу, атом, атомное ядро, элементарную частицу). Квантовые числа отражают дискретность (квантованность) физических величин, характеризующих микросистему. Набор квантовых чисел, исчерпывающе описывающих микросистему, называют полным.                                  Основные квантовые числа:                       n Главное квантовое число: n = 1, 2, … 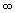.; j-Квантовое число полного углового момента. j никогда не бывает отрицательным и может быть целым (включая ноль) или полуцелым в зависимости от свойств рассматриваемой системы. Величина полного углового момента J связана с j соотношением J² = ћ²j(j + 1). 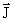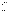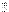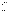= + , где и 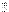векторы орбитального и спинового угловых моментов;  l -Квантовое число орбитального углового момента l может принимать только целые значения: l = 0, 1, 2, … ∞. Величина орбитального углового L момента связана с l соотношением L² = ћ²l(l + 1).; m-Магнитное квантовое число. Проекция полного, орбитального или спинового углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m_j = j, j-1, j-2, …, - (j-1), - j. Для орбитального момента m_l = l, l-1, l-2, …, -(l-1), -l.
Для спинового момента электрона, протона, нейтрона, кварка m_s = ±1/2 s - Квантовое число спинового углового момента s может быть либо целым, либо полуцелым.; s - неизменная характеристика частицы,
определяемая ее свойствами. Величина спинового момента S связана с s соотношением S² = ћ²s(s + 1).; P -Пространственная четность. Она равна либо +1, либо -1 и характеризует поведение системы при зеркальном отражении. P = (-1)^l.                           2) Спин-это собственный момент импульса. Спиновый момент импульса электрона определяется формулой 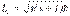                                  Здесь s–спиновое квантовое число. Спиновое квантовое число имеет только одно значение  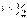Проекция спина на направление внешнего магнитного поля может принимать значения 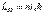где 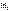- магнитное спиновое число. Так как существует всего 2 ориентации спинового момента на направление внешнего поля, то m_S = ±1/2.     В 1925 г. Паули установил квантово-механический закон, называемый принципом Паули или принципом исключения. Простейшая формулировка принципа Паули заключается в следующем. В любой системе, содержащей множество электронов, не может быть более одного электрона с одинаковым набором четырех квантовых чисел n, l, m, m_S: 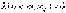или

Принцип Паули справедлив для всех частиц, для которых 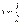. Эти частицы называют фермионами.