КОЛЕБАНИЯ И ВОЛНЫ
3) ЭЛЕКТРИЧЕСКИМ КОЛЕБАТЕЛЬНЫМ КОНТУРОМ называется электрическая цепь, состоящая из включенных последовательно катушки индуктивностью L , конденсатора емкостью C и резистора сопротивлением R . По закону Ома для участка цепи 
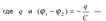 заряд конденсатора и разность потенциалов его обкладок в произвольный момент времени t; R − электрическое сопротивление колебательного контура; Θc − ЭДС самоиндукции в катушке. Сила тока
заряд конденсатора и разность потенциалов его обкладок в произвольный момент времени t; R − электрическое сопротивление колебательного контура; Θc − ЭДС самоиндукции в катушке. Сила тока 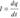 , поэтому дифференциальное уравнение колебаний заряда в колебательном контуре:
, поэтому дифференциальное уравнение колебаний заряда в колебательном контуре: 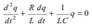
ВОЛНОВОЙ ПРОЦЕСС.
Если возбудить колебания в какой-либо точке среды (твердой, жидкой или газообразной) то, вследствие взаимодействия между частицами среды, эти колебания будут передаваться от одной точки среды к другой со скоростью, зависящей от свойств среды. При рассмотрении колебаний не учитывается детальное строение среды; среда рассматривается как сплошная, непрерывно распределенная в пространстве и обладающая упругими свойствами. Среда называется линейной, если ее свойства не изменяются под действием возмущений, создаваемых колебаниями. Волновым процессом или волной — называется процесс распространения колебаний в сплошной среде. При распространении волны частицы колеблются около своих положений равновесия, а не перемещаются вслед за волной. Вместе с волной от частицы к частице передается только состояние колебательного движения и его энергия. Основным свойством всех волн является перенос энергии без переноса вещества.
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими.
Отличие графика волны от графика гармонического колебания:
1) график волны представляет зависимость смещения всех частиц среды от расстояния до
источника колебаний в данный момент времени ξ= ξ (x,t=const );
2) график гармонического колебания это зависимость смещения данной частицы от
времени ξ =ξ(x = const,t).
Бегущими волнами называются волны, которые переносят в пространстве энергию.
Перенос энергии количественно характеризуется вектором плотности потока энергии (вектор Умова). Направление этого вектора совпадает с направлением распространения энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно волне. Важными примерами бегущих волн являются плоская и сферическая волны. Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу.
Волна называется сферической, если ее волновые поверхности имеют вид концентрических сфер. Центры этих сфер называются центром волны.
11) Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных: 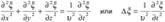 где υ — фазовая скорость,
где υ — фазовая скорость, 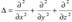 — оператор Лапласа Решением волнового уравнения является уравнение любой волны (в том числе и плоская и сферическая волны). Интерференцией волн называется явление наложения волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других в зависимости от соотношения между фазами этих волн. Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками, колеблющимися с одинаковыми амплитудой A0, частотой ω и постоянной разностью фаз:
— оператор Лапласа Решением волнового уравнения является уравнение любой волны (в том числе и плоская и сферическая волны). Интерференцией волн называется явление наложения волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других в зависимости от соотношения между фазами этих волн. Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками, колеблющимися с одинаковыми амплитудой A0, частотой ω и постоянной разностью фаз:
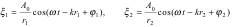 где r1 и r2 — расстояния от источников до рассматриваемой точки, k — волновое число, ϕ1 и ϕ2 — начальные фазы волн.
где r1 и r2 — расстояния от источников до рассматриваемой точки, k — волновое число, ϕ1 и ϕ2 — начальные фазы волн.
Поскольку для когерентных источников ϕ1 − ϕ2 = const , то результат интерференции двух волн зависит от величины (r1 − r2) , называемой разностью хода. Интерференционный максимум (A = A0/r1 + A0/r2) наблюдается в точках, где k(r1 − r2) − (ϕ1 −ϕ2) = ±2m (m = 0,1, 2,K) π Интерференционный минимум (A = |A0/r1 - A0/r2|) наблюдается в точках, где k(r1 − r2) − (ϕ1 −ϕ2) = ±(2m +1)π
ОПТИКА
ГЕОМЕТР . ОПТИКА
Оптика — раздел физики, который изучает природу света, световые явления и взаимодействие света с веществом. Оптическое излучение представляет собой электромагнитные волны, и поэтому оптика является частью общего учения об электромагнитном поле. В зависимости от круга рассматриваемых явлений оптику делят на геометрическую лучевую), волновую физическую), квантовую (корпускулярную). Основные законы геометрической оптики. Еще до установления природы света были известны следующие законы: Закон прямолинейного распространения света — свет в оптически однородной среде распространяется прямолинейно. Световой луч — линия, вдоль которой переносится световая энергия. В однородной среде лучи света представляют собой прямые линии. Закон независимости световых пучков — эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены. Закон отражения — отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения; угол отражения i1′ равен углу падения I1: 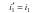 .
.
Закон преломления — луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела двух сред в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред 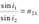 , где n21— относительный показатель преломления второй среды относительно первой, который равен отношению абсолютных показателей преломления двух сред
, где n21— относительный показатель преломления второй среды относительно первой, который равен отношению абсолютных показателей преломления двух сред 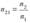 . Следовательно, закон преломления будет иметь вид:
. Следовательно, закон преломления будет иметь вид: 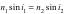 Абсолютным показателем преломления среды называется величина n , равная
Абсолютным показателем преломления среды называется величина n , равная 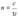 отношению скорости электромагнитных волн в вакууме c к их фазовой скорости υ в среде. Поскольку υ = c εµ , то n = εµ , где ε и µ — соответственно электрическая и магнитная проницаемость среды.
отношению скорости электромагнитных волн в вакууме c к их фазовой скорости υ в среде. Поскольку υ = c εµ , то n = εµ , где ε и µ — соответственно электрическая и магнитная проницаемость среды.
Энергетические величины в фотометрии. Фотометрия — раздел оптики, в котором рассматриваются энергетические характеристики оптического излучения в процессах его испускания, распространения и взаимодействия с веществом. При этом значительное внимание уделяется вопросам измерения интенсивности света и его источников. Энергетические величины в фотометрии — характеризуют энергетические параметры оптического излучения без учета особенностей его воздействия на тот или иной приемник излучения. Поток излучения Φ e — величина, равная отношению энергии W излучения ко времени t , за которое излучение произошло (мощность излучения). Единица потока излучения — ватт (Вт) 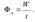 .
.
Энергетическая светимость (излучательность) R e -величина, равная отношению потока излучения Φ e, испускаемого поверхностью, к площади S сечения, сквозь которое этот поток проходит (поверхностная плотность потока излучения). Единица энергетической светимости — ватт на метр в квадрате (Вт/м2) 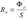 . Энергетическая сила света (сила излучения) Ie — величина, равная отношению потока излучения Φe точечного источника к телесному углу ω , в пределах которого это излучение распространяется. Единица энергетической силы света — ватт на стерадиан (Вт/ср).
. Энергетическая сила света (сила излучения) Ie — величина, равная отношению потока излучения Φe точечного источника к телесному углу ω , в пределах которого это излучение распространяется. Единица энергетической силы света — ватт на стерадиан (Вт/ср). 
Энергетическая яркость (лучистость) Be — величина, равная отношению энергетической силы света ∆Ie элемента излучающей поверхности к площади ∆S проекции этого элемента на плоскость, перпендикулярную направлению наблюдения. Единица энергетической яркости — ватт на стерадиан-метр в квадрате (Вт/(ср·м2)). 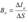 Энергетическая освещенность (облученность) Ee — характеризует величину потока излучения, падающего на единицу освещаемой поверхности. Единица энергетической освещенности — ватт на метр в квадрате (Вт/м2).
Энергетическая освещенность (облученность) Ee — характеризует величину потока излучения, падающего на единицу освещаемой поверхности. Единица энергетической освещенности — ватт на метр в квадрате (Вт/м2).
Световые величины в фотометрии. Различные приемники, используемые при оптических измерениях, обладают селективностью (избирательностью). Для каждого из них характерна своя кривая чувствительности к энергии различных длин волн. Световые измерения, являясь субъективными, отличаются от объективных, энергетических, и для них вводятся световые единицы, используемые только для видимого света. Основной световой единицей в СИ является единица силы света I — кандела (кд) — сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540·1012 герц, энергетическая сила света которого в этом направлении составляет 1683 Вт/ср. Единица светового потока Φ (мощности оптического излучения) — люмен (лм): 1лм — световой поток, испускаемый точечным источником силой света в 1кд внутри телесного угла в 1ср (1лм=1кд·ср). Светимость R — суммарный поток, посылаемый светящейся площадкой с площадью S . Единица светимости — люмен на метр в квадрате (лм/м2)  Яркость светящейся поверхности в некотором направлении ϕ есть величина, равная отношению силы света I в этом направлении к площади S проекции светящейся поверхности на плоскость, перпендикулярную данному направлению. Единица яркости — кандела на метр в квадрате (кд/м2).
Яркость светящейся поверхности в некотором направлении ϕ есть величина, равная отношению силы света I в этом направлении к площади S проекции светящейся поверхности на плоскость, перпендикулярную данному направлению. Единица яркости — кандела на метр в квадрате (кд/м2). 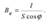 Освещенность E — величина, равная отношению светового потока Φ , падающего на поверхность, к площади S этой поверхности. Единица освещенности — люкс (лк): 1лк — освещенность поверхности, на один квадратный метр которой падает световой поток в 1лм (1лк=1лм/м2).
Освещенность E — величина, равная отношению светового потока Φ , падающего на поверхность, к площади S этой поверхности. Единица освещенности — люкс (лк): 1лк — освещенность поверхности, на один квадратный метр которой падает световой поток в 1лм (1лк=1лм/м2). 
2. ЛИНЗОЙ называется прозрачное тело, ограниченное с двух сторон криволинейной поверхностью
(В частном случае одна из поверхностей может быть плоской). По внешней форме линзы делятся на 1) двояковыпуклые; 2) плосковыпуклые; 3) двояковогнутые; 4) плосковогнутые; 5) выпукло-вогнутые. Линза называется тонкой, если ее толщина значительно меньше, чем радиусы кривизны R1 и R2 обеих поверхностей. На оптических схемах линзы обычно обозначают двунаправленной стрелкой. Радиус кривизны R > 0 для выпуклой поверхности; R < 0 для вогнутой.
Прямая проходящая через центры кривизны поверхностей линзы называется главной оптической осью. Оптическим центром линзы (обычно обозначается O ) называется точка, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь.
Побочными оптическими осями называются прямые, проходящие через оптический центр линзы и не совпадающие с главной оптической осью. Фокусом линзы F называется точка, лежащая на главной оптической оси, в которой пересекаются лучи параксиального (приосевого) светового пучка, распространяющиеся параллельно главной оптической оси. Фокальной плоскостью называется плоскость, проходящая через фокус линзы перпендикулярно ее главной оптической оси.
Фокусным расстоянием f называется расстояние между оптическим центром линзы O и ее фокусом F : 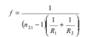
Формула тонкой линзы: 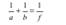 где a и b — расстояния от линзы до предмета и его изображения. Если a = ∞ , т.е. лучи падают на линзу параллельным пучком (а), то b = f . Если b = ∞ , т.е. изображении находится в бесконечности (б), и, следовательно, лучи выходят из линзы параллельным пучком, то a = f . Фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны. Величина Φ =1 f называется оптической силой линзы. Ее единица —диоптрия (дптр) — оптическая сила линзы с фокусным расстоянием 1м
где a и b — расстояния от линзы до предмета и его изображения. Если a = ∞ , т.е. лучи падают на линзу параллельным пучком (а), то b = f . Если b = ∞ , т.е. изображении находится в бесконечности (б), и, следовательно, лучи выходят из линзы параллельным пучком, то a = f . Фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны. Величина Φ =1 f называется оптической силой линзы. Ее единица —диоптрия (дптр) — оптическая сила линзы с фокусным расстоянием 1м
Линзы с положительной оптической силой являются собирающими, с отрицательной —рассеивающими. В отличие от собирающей линзы, рассеивающая линза имеет мнимые фокусы. В мнимом фокусе сходятся после преломления) воображаемые продолжения лучей, падающих на рассеивающую линзу параллельно главной оптической оси.
Аберрации оптических систем. В реальных оптических системах используются пучки отличающиеся от параксиальных, показатель преломления линз зависит от длины волны падающего света, а сам свет немонохроматичен. Искажения оптического изображения которые возникают при этом называются аберрациями.
Сферическая аберрация. Фокус S′′ для лучей, более удаленных от оптической оси чем параксиальные, находится ближе, чем фокус S′ параксиальных лучей. В результате изображение светящейся точки имеет вид расплывчатого пятна. Сферическая аберрация является частным случаем астигматизма.
Кома. Если через оптическую систему проходит широкий пучок от точечного источника света, расположенного не на оптической оси, то получаемое изображение этой точки будет в виде освещенного пятна неправильной формы.
Точечным источником света называется источник, размерами которого можно пренебречь.
Астигматизм. Погрешность, обусловленная неодинаковостью кривизны оптической поверхности в разных плоскостях сечения падающего на нее светового пучка
Дисторсия. Погрешность, при которой при больших углах падения лучей на линзу линейное увеличение для точек предмета, которые находятся на разных расстояниях от главной оптической оси, несколько различается. В результате нарушается геометрическое подобие между предметом (например, прямоугольная сетка) и его изображением р(исунок (b) —подушкообразная дисторсия, (c) — бочкообразная дисторсия).
Хроматическая аберрация.При падении на оптическую систему белого света отдельные составляющие его монохроматические лучи фокусируются в разных точках н(аибольшее фокусное расстояние имеют красные лучи, наименьшее — фиолетовые), поэтому изображение размыто и по краям окрашено.
3. ИНТЕРФЕРЕНЦИЯ СВЕТА. Интерференция света — сложение в пространстве двух или нескольких когерентных световых волн, при котором в разных его точках получается усиление или ослабление амплитуды результирующей волны. Пусть в данной точке M две монохроматические волны с циклической частотой ω возбуждают два колебания, причем до точки M одна волны прошла в среде с показателем преломления n1 путь s1 с фазовой скоростью υ1 , а вторая — в среде n2 путь s2 с фазовой скоростью υ2 :  Амплитуда результирующего колебания:
Амплитуда результирующего колебания: 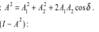
Интенсивность результирующей волны : 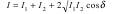
Разность фаз δ колебаний, возбуждаемых в точке M , равна 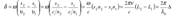
(Использовали: υ = c n ; ω = 2πν ; c ν = λ0 — длина волны в вакууме). Произведение геометрической длины пути s световой волны в данной среде на показатель преломления этой среды n называется оптической длиной пути L = s ⋅ n. Разность ∆ = L2 − L1 = s2n2 − s1n1 оптических длин проходимых волнами путей называется оптической разностью хода. Условие интерференционного максимума: Если оптическая разность хода ∆ равна целому числу длин волн в вакууме (четному числу полуволн)
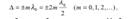 то δ = ±2mπ и колебания, возбуждаемые в точке M , будут происходить в одинаковой фазе. Условие интерференционного минимума. Если оптическая разность хода ∆ равна нечетному числу полуволн
то δ = ±2mπ и колебания, возбуждаемые в точке M , будут происходить в одинаковой фазе. Условие интерференционного минимума. Если оптическая разность хода ∆ равна нечетному числу полуволн
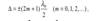 то δ = ±(2m +1)π и колебания, возбуждаемые в точке M , будут
то δ = ±(2m +1)π и колебания, возбуждаемые в точке M , будут
происходить в противофазе.
Методы наблюдения интерференции. До изобретения лазеров, во всех приборах когерентные световые пучки получали разделением волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладывали друг на друга и наблюдали интерференционную картину.
1. Метод Юнга. Свет от ярко освещенной щели S падает на две щели S1 и S2, играющие роль когерентных источников. Интерференционная картина BC наблюдается на экране Э.
2. Зеркала Френеля. Свет от источника S падает расходящимся пучком на два плоских зеркала A1O и A2O , расположенных под малым углом ϕ . Роль когерентных источников играют мнимые S1 и S2 изображения источника S . Интерференционная картина наблюдается на экране Э, защищенном от прямого попадания света заслонкой З.
3.Бипризма Френеля. Свет от источника S преломляется в призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых когерентных источников S1 и S2.
4. Зеркало Ллойда. Точечный источник S находится близко к поверхности плоского зеркала M . Когерентными источниками служат сам источник S и его мнимое изображение S1.
Кольца Ньютона. Кольца Ньютона, являющиеся классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны. Параллельный пучок света падает нормально на плоскую поверхность линзы. Полосы равной толщины имеют вид концентрических окружностей. С учетом d2 → 0
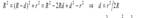 В отраженном свете оптическая разность хода:
В отраженном свете оптическая разность хода: 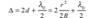
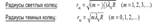
Интерференцию можно наблюдать и в проходящем свете, причем в проходящем свете максимумы интерференции соответствуют минимумам интерференции в отраженном свете и наоборот.
4. ПРОСВЕТЛЕНИЕ ОПТИКИ. Объективы оптических приборов содержат большое количество линз. Даже незначительное отражение света каждой из поверхностей линз приводит к тому, что интенсивность прошедшего пучка света значительно уменьшается. Кроме того, в объективах возникают блики и фон рассеянного света, что снижает эффективность оптических систем. Но, если на границах сред создать условия, при которых интерференция отраженных лучей 1’ и 2" дает минимум интенсивности отраженного света, то при этом интенсивность света, прошедшего через оптическую систему будет максимальна. Этого можно добиться, например, нанесением на поверхность линз тонких пленок с показателем преломления 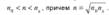 . В этом случае амплитуды когерентных лучей 1’ и 2" будут одинаковы, а условие минимума для отраженных лучей (i = 0) будет
. В этом случае амплитуды когерентных лучей 1’ и 2" будут одинаковы, а условие минимума для отраженных лучей (i = 0) будет 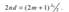 . При m = 0 оптическая толщина пленки nd удовлетворяет условию
. При m = 0 оптическая толщина пленки nd удовлетворяет условию 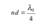 и происходит гашение отраженных лучей. Для каждой длины волны λ0 должна быть своя толщина пленки d . Поскольку этого добиться невозможно, обычно оптику просветляют для длины волны λ0 = 550 нм, к которой наиболее чувствителен глаз человека.
и происходит гашение отраженных лучей. Для каждой длины волны λ0 должна быть своя толщина пленки d . Поскольку этого добиться невозможно, обычно оптику просветляют для длины волны λ0 = 550 нм, к которой наиболее чувствителен глаз человека.
Информетры. При плавном изменении разности хода интерферирующих пучков на λ/2интерференционная картина сместится настолько, что на месте максимумов окажутся минимумы. Поэтому явление интерференции используют в интерферометрах для измерения длины тел, длины световой волны, изменения длины тела при изменении температуры, сравнимых с λ0
В интерферометре Майкельсона монохроматический луч от источника S разделяется на полупрозрачной пластинке P1 на два луча 1’ и 2", которые, отразившись от зеркал M1 и M2 , снова с помощью P1 сводятся в один пучок, в котором лучи 1' и 2" формируют интерференционную картину. Компенсационная пластинка P2 размещается на пути луча 2, чтобы он так же, как и луч 1, дважды прошел через пластинку. Возникающая интерференционная картина чрезвычайно чувствительна к любому изменению разности хода лучей, (например, к смещению одного из зеркал).
5. ПРИНЦИП ГЮЙГЕНСА-ФРЕНЕЛЯ. Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле — любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Дифракцию объясняет принцип Гюйгенса — именно вторичные волны огибают препятствия на пути распространения первичных волн. Френель дополнил принцип Гюйгенса представлением о когерентности вторичных волн и их интерференции. Согласно принципу Гюйгенса-Френеля, световая волна, возбуждаемая каким-либо источником S , может быть представлена как результат суперпозиции (сложения) когерентных вторичных волн, излучаемых вторичными (фиктивными) источниками — бесконечно малыми элементами любой замкнутой поверхности, охватывающей источник S .
18. Зоны Френеля. Рассмотрим в произвольной точке M амплитуду световой волны, распространяющейся в однородной среде из точечного источника S . Согласно принципу Гюйгенса-Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Φ , являющейся поверхностью фронта волны, идущей из S (поверхность сферы с центром S). Разобьем волновую поверхность Φ на кольцевые зоны такого размера, чтобы расстояния от краев зоны до M отличались на λ/2.
Тогда, обозначив амплитуды колебаний от 1-й, 2-й, … m-й зон через A1, A2, …Aм (при этом A1 > A2 > A3 >K), получим амплитуду результирующего колебания: A = A1 − A2 + A3 − A4 + K. При таком разбиении волновой поверхности на зоны оказывается, что амплитуда колебания Am от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон
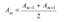

Радиус внешней границы m-й зоны Френеля 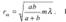 При ab= = 10см и λ = 500нм радиус первой зоны r1 = 0,158мм. Следовательно, распространение света от S к M происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SM , т.е. прямолинейно. Таким образом, принцип Гюйгенса-Френеля позволяет объяснить прямолинейное распространение света в однородной среде.
При ab= = 10см и λ = 500нм радиус первой зоны r1 = 0,158мм. Следовательно, распространение света от S к M происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SM , т.е. прямолинейно. Таким образом, принцип Гюйгенса-Френеля позволяет объяснить прямолинейное распространение света в однородной среде.
6. ДИФРАКЦИЯ НА ПРОСТРАНСТВЕННОЙ РЕШЕТКЕ. Дифракция света наблюдается на одномерных решетках (система параллельных штрихов), на двумерных решетках (штрихи нанесены во взаимно перпендикулярных направлениях в одной и той же плоскости) и на пространственных (трехмерных) решетках — пространственных образованиях, в которых элементы структуры подобны по форме, имеют геометрически правильное и периодически повторяющееся расположение, а также постоянные (периоды) решеток, соизмеримые с длиной волны электромагнитного излучения. Кристаллы, являясь трехмерными пространственными образованиями с постоянной решетки порядка 10–10м, могут быть использованы для наблюдения дифракции рентгеновского излучения (λ ≈10−12 ч10−8м) . Представим кристалл в виде параллельных кристаллографических плоскостей, отстоящих друг от друга на расстоянии d . Пучок параллельных монохроматических лучей (1, 2) падает под углом скольжения ϑ (угол между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн (1’ и 2’), интерферирующих между собой. Максимумы интенсивности будут наблюдаться в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе: 2d sinϑ = mλ (m =1,2,3,K) — формула Вульфа–Брэггов. Эта формула используется в: 1) рентгеноструктурном анализе — если известна λ рентгеновского излучения, то, наблюдая дифракцию на кристаллической структуре неизвестного строения и измеряя ϑ и m , можно найти d , т.е. определить структуру вещества; 2) рентгеновской спектроскопии — если известна d , то измеряя ϑ и m, можно найти длину волны λ падающего рентгеновского
7. ДИСПЕРСИЯ СВЕТА. Дисперсией света называется зависимость показателя преломления n от частоты ν (длины волны λ ) света (или зависимость фазовой скорости υ световых волн от его частоты ν ). Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму. Дисперсия проявляется лишь при распространении немонохроматических волн.
Для всех прозрачных веществ показатель преломления уменьшается с увеличением длины волны: dn/dλ<0 (см. рисунок). Такая дисперсия называется нормальной (или отрицательной). Вблизи линий и полос сильного поглощения ход кривой n(λ) — кривой дисперсии — обратный:dn/dλ>0. Такая дисперсия называется аномальной.
На явлении нормальной дисперсии основано действие призменных спектрографов. Угол отклонения лучей призмой зависит от показателя преломления, который в свою очередь, зависит от длины волны. Поэтому призма разлагает белый свет в спектр, отклоняя красные лучи (длина волны больше) слабее, чем фиолетовые (длина волны меньше).
Электронная теория дисперсии. Электронная теория дисперсии Лоренца рассматривает дисперсию света как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны. Абсолютный показатель преломления среды n = 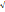 εµ , где ε — диэлектрическая проницаемость среды, µ — магнитная проницаемость. В оптической области спектра для всех веществ µ ≈1, поэтому n =
εµ , где ε — диэлектрическая проницаемость среды, µ — магнитная проницаемость. В оптической области спектра для всех веществ µ ≈1, поэтому n = 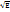 Согласно теории Лоренца, дисперсия света — следствие зависимости ε от частоты (длины волны) световых волн. По определению
Согласно теории Лоренца, дисперсия света — следствие зависимости ε от частоты (длины волны) световых волн. По определению 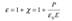 , где χ — диэлектрическая восприимчивость среды, ε0 — электрическая постоянная, P и E — мгновенные значение поляризованности и напряженности внешнего электрического поля. В оптической области спектра частота колебаний электрического поля световой волны высока (ν ≈1013Гц), поэтому ориентационная поляризация диэлектриков несущественна, и главную роль играет электронная (деформационная) поляризация — вынужденные колебания электронов под действием электрической составляющей поля световой волны. Пусть вынужденные колебания совершает только один внешний, слабо связанный с ядром атома, электрон — оптический электрон. Его наведенный дипольный момент: p = ex , где e — заряд электрона, x — смещение электрона под действием электрического поля световой волны. Мгновенное значение поляризованности: P = n0 p = n0ex , где n0- концентрация атомов в диэлектрике. Отсюда: ∆λ/2 зон. Все точки волнового фронта в плоскости щели имеют одинаковую фазу и амплитуду колебаний. Поэтому суммарная интенсивность колебаний от двух любых соседних зон Френеля равна нулю. Следовательно: 1) если число зон Френеля четное, то:
, где χ — диэлектрическая восприимчивость среды, ε0 — электрическая постоянная, P и E — мгновенные значение поляризованности и напряженности внешнего электрического поля. В оптической области спектра частота колебаний электрического поля световой волны высока (ν ≈1013Гц), поэтому ориентационная поляризация диэлектриков несущественна, и главную роль играет электронная (деформационная) поляризация — вынужденные колебания электронов под действием электрической составляющей поля световой волны. Пусть вынужденные колебания совершает только один внешний, слабо связанный с ядром атома, электрон — оптический электрон. Его наведенный дипольный момент: p = ex , где e — заряд электрона, x — смещение электрона под действием электрического поля световой волны. Мгновенное значение поляризованности: P = n0 p = n0ex , где n0- концентрация атомов в диэлектрике. Отсюда: ∆λ/2 зон. Все точки волнового фронта в плоскости щели имеют одинаковую фазу и амплитуду колебаний. Поэтому суммарная интенсивность колебаний от двух любых соседних зон Френеля равна нулю. Следовательно: 1) если число зон Френеля четное, то: 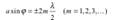 — условие дифракционного минимума (полная темнота).
— условие дифракционного минимума (полная темнота).
2) если число зон Френеля нечетное, то 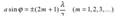 — условие дифракционного максимума,соответствующего действию одной некомпенсированной зоны Френеля. В направлении ϕ = 0 щель действует как одна зона Френеля и в этом направлении свет распространяется с наибольшей интенсивностью — центральный дифракционный максимум. Направления, в которых амплитуда максимальна или равна нулю:
— условие дифракционного максимума,соответствующего действию одной некомпенсированной зоны Френеля. В направлении ϕ = 0 щель действует как одна зона Френеля и в этом направлении свет распространяется с наибольшей интенсивностью — центральный дифракционный максимум. Направления, в которых амплитуда максимальна или равна нулю:
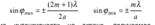 Распределение интенсивности на экране, получаемое вследствие дифракции, называется дифракционным спектром (рисунок (б)). Интенсивности в центральном и последующих максимумах относятся как 1: 740,0:710,0:3800,0:…, т.е. основная часть световой энергии сосредоточена в центральном максимуме. Положение дифракционных максимумов зависит от λ . При освещении щели белым светом, центральный максимум наблюдается в виде белой полоски (при ϕ = 0 разность хода равна нулю для всех λ ) — он общий для всех длин волн. Боковые максимумы радужно окрашены фиолетовым краем к центру дифракционной картины (поскольку λфиол < λкрасн ).
Распределение интенсивности на экране, получаемое вследствие дифракции, называется дифракционным спектром (рисунок (б)). Интенсивности в центральном и последующих максимумах относятся как 1: 740,0:710,0:3800,0:…, т.е. основная часть световой энергии сосредоточена в центральном максимуме. Положение дифракционных максимумов зависит от λ . При освещении щели белым светом, центральный максимум наблюдается в виде белой полоски (при ϕ = 0 разность хода равна нулю для всех λ ) — он общий для всех длин волн. Боковые максимумы радужно окрашены фиолетовым краем к центру дифракционной картины (поскольку λфиол < λкрасн ).
8. ЕСТЕСТВЕННЫЙ И ПОЛЯРИЗОВАННЫЙ СВЕТ. При действии света на вещество основное значение имеет электрическая составляющая электромагнитного поля световой волны, поскольку именно она оказывает основное действие на электроны в атомах вещества. Поэтому, для описания закономерностей поляризации будем рассматривать только световой вектор — вектор напряженности E электрического поля.
Свет представляет собой суммарное электромагнитное излучение множества независимо излучающих атомов. Поэтому все ориентации вектора E будут равновероятны. Такой свет называется естественным (рис. (а)).
Поляризованным светом называется свет, в которомнаправления колебания вектора E каким-либо образом упорядочены. Частично поляризованный свет (рис. (б)) — свет с
преимущественным направлением колебаний вектора E.
Плоскополяризованный свет — свет в котором вектор E колеблется только в одной, проходящей через луч плоскости (рис. (в) на предыдущей странице и рис. (а) и (б) на этой).
Эта плоскость называется плоскостью поляризации. Если концы вектора E с течением времени описывают в плоскости, перпендикулярной лучу,окружность или эллипс (рис.(в)), то свет называется циркулярно или эллиптически поляризованным. Степенью поляризации называется величина P : 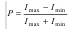 , где
, где 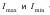 — соответственно, максимальная и минимальная интенсивности частично поляризованного света. Для естественного света
— соответственно, максимальная и минимальная интенсивности частично поляризованного света. Для естественного света 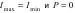 , для плоскополяризованного I min = 0 и P =1. Естественный свет можно преобразовать в плоскополяризованный, используя так называемые поляризаторы, пропускающие колебания только определенного направления. В качестве поляризаторов используются среды, анизотропные в отношении вектора колебаний E.
, для плоскополяризованного I min = 0 и P =1. Естественный свет можно преобразовать в плоскополяризованный, используя так называемые поляризаторы, пропускающие колебания только определенного направления. В качестве поляризаторов используются среды, анизотропные в отношении вектора колебаний E.
Закон Малюса.
Пропустим естественный свет с интенсивностью Iест через поляризатор T1. Колебание амплитуды A, совершающееся в плоскости, образующей с плоскостью поляризатора угол ϕ , можно разложить на два колебания с амплитудами A = Acosϕ и A⊥ = Asinϕ . Интенсивность прошедшей волны пропорциональна 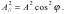 . В естественном свете все значения ϕ равновероятны, поэтому доля света, прошедшего через поляризатор, будет равна среднему значению (cos2ϕ) = 1/2, а интенсивность плоскополяризованного света, прошедшего через первый поляризатор T1:
. В естественном свете все значения ϕ равновероятны, поэтому доля света, прошедшего через поляризатор, будет равна среднему значению (cos2ϕ) = 1/2, а интенсивность плоскополяризованного света, прошедшего через первый поляризатор T1: 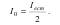
Поставим на пути плоскополяризованного света второй поляризатор T2 (анализатор) под углом ψ к первому. Интенсивность I света, прошедшего через анализатор, меняется в зависимости от угла ψ по закону Малюса  Следовательно, интенсивность света, прошедшего через два поляризатора:
Следовательно, интенсивность света, прошедшего через два поляризатора: 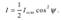 .
. 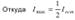 когда поляризаторы параллельны и Imin = 0 , когда поляризаторы скрещены.
когда поляризаторы параллельны и Imin = 0 , когда поляризаторы скрещены.
Абсолютно черное тело.
Тело, способное поглощать при любой температуре всё падающее на него излучение любой частоты называется абсолютно черным телом.
Спектральная поглощательная способность черного тела для всех частот и температур тождественно равна единице 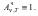 Абсолютно черных тел в природе нет, однако такие тела, как сажа и черный бархат в определенном интервале частот близки к ним. Идеальной моделью черного тела является замкнутая полость с небольшим отверстием O , внутренняя поверхность которой зачернена. Луч, попавший внутрь такой полости, полностью поглощается. Наряду с понятием черного тела используют понятие серого тела —тела, поглощательная способность которого меньше единицы, но одинакова для всех частот и зависит только от температуры, материала и состояния поверхности тела:
Абсолютно черных тел в природе нет, однако такие тела, как сажа и черный бархат в определенном интервале частот близки к ним. Идеальной моделью черного тела является замкнутая полость с небольшим отверстием O , внутренняя поверхность которой зачернена. Луч, попавший внутрь такой полости, полностью поглощается. Наряду с понятием черного тела используют понятие серого тела —тела, поглощательная способность которого меньше единицы, но одинакова для всех частот и зависит только от температуры, материала и состояния поверхности тела: 
Закон Кирхгофа. Закон Кирхгофа определяет соотношение между испускательной и поглощательной способностями тел. Отношение испускательной и поглощательной способностей тела не зависит от природы тела и является универсальной для всех тел функцией частоты и температуры Rv,t 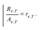
Для черного тела  , поэтому универсальная функция Кирхгофа R ν,t есть спектральная плотность энергетической светимости (испускательная способность) черного тела. Нахождение явной зависимости Rν,t от частоты и температуры является важной задачей теории теплового излучения.
, поэтому универсальная функция Кирхгофа R ν,t есть спектральная плотность энергетической светимости (испускательная способность) черного тела. Нахождение явной зависимости Rν,t от частоты и температуры является важной задачей теории теплового излучения.
12. ЗАКОН СТЕФАНА-БОЛЬЦМАНА. Энергетическая светимость серого тела (интегральная по ν ):
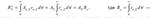 энергетическая светимость черного тела, которая зависит только от температуры.
энергетическая светимость черного тела, которая зависит только от температуры.
 Эту зависимость описывает экспериментальный закон Стефана-Больцмана: энергетическая светимость черного тела пропорциональна четвертой степени термодинамической температуры:
Эту зависимость описывает экспериментальный закон Стефана-Больцмана: энергетическая светимость черного тела пропорциональна четвертой степени термодинамической температуры: 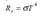
где 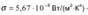 — постоянная Стефана-Больцмана.
— постоянная Стефана-Больцмана.
Закон Вина. Закон Стефана-Больцмана ничего не говорит о спектральном составе излучения черного тела. Положение максимума в спектре его излучения описывается экспериментальным законом смещения Вина: Длина волны λmax , при которой излучательная способность Rλ,t черного тела максимальна, обратно пропорциональна его термодинамической температуре: 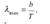 ,где
,где 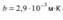 — постоянная Вина. Ультрафиолетовая катастрофа (Формулы Рэлея-Джинса и Вина).
— постоянная Вина. Ультрафиолетовая катастрофа (Формулы Рэлея-Джинса и Вина).
Применяя к тепловому излучению классический закон равнораспределения энергии по степеням свободы Рэлей и Джинс получили выражение для зависимости испускательной способности черного тела Rν,t от частоты света 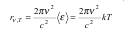
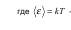 — средняя энергия осциллятора с собственной частотой ν. Однако попытка получить закон Стефана-Больцмана из этой формулы приводит к абсурдному результату — Re неограниченно растет, достигая чрезвычайно больших значений в ультрафиолете, — который получил название "ультрафиолетовая катастрофа":
— средняя энергия осциллятора с собственной частотой ν. Однако попытка получить закон Стефана-Больцмана из этой формулы приводит к абсурдному результату — Re неограниченно растет, достигая чрезвычайно больших значений в ультрафиолете, — который получил название "ультрафиолетовая катастрофа":
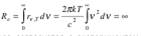
Формула Рэлея-Джинса согласуется с экспериментом только в области малых частот и больших температур. В области больших частот хорошо описывает эксперимент формула Вина (закон излучения Вина):  13. КВАНТОВАЯ ГИПОТЕЗА ПЛАНКА. Макс Планк предположил, что теория классического гармонического осциллятора неприменима к атомным осцилляторам; атомные осцилляторы излучают энергию не непрерывно, а определенными порциями — квантами.
13. КВАНТОВАЯ ГИПОТЕЗА ПЛАНКА. Макс Планк предположил, что теория классического гармонического осциллятора неприменима к атомным осцилляторам; атомные осцилляторы излучают энергию не непрерывно, а определенными порциями — квантами.
Энергия кванта: 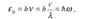

В механике есть имеющая размерность "энергияЧвремя" величина, которая называется действием. Поэтому постоянную Планка иногда называют квантом действия. Размерность h совпадает с размерностью момента импульса. Поскольку энергия излучается порциями, то энергия осциллятора может принимать лишь определенные дискретные значения, кратные целому числу квантов: ε = nhν (n = 1, 2, K)
Среднюю энергию осцилляторов ε нельзя принимать равной kT . Планкиспользовал распределение Больцмана частиц по энергиям. Тогда вероятность Pi того, что энергия колебания осциллятора частоты ν имеет значение Ei определяется выражением 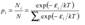 , где Ni — число осцилляторов с энергией εi, N — полное число осцилляторов. Отсюда можно получить выражение для средней энергии осцилляторов
, где Ni — число осцилляторов с энергией εi, N — полное число осцилляторов. Отсюда можно получить выражение для средней энергии осцилляторов 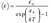 . Тогда универсальная функция Кирхгофа rν,T будет иметь вид
. Тогда универсальная функция Кирхгофа rν,T будет иметь вид 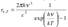 — формула Планкa.
— формула Планкa.
В области малых частот hν << kT 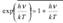 формула Планка переходит в формулу Рэлея-Джинса. Закон Стефана-Больцмана
формула Планка переходит в формулу Рэлея-Джинса. Закон Стефана-Больцмана 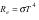 получается из формулы Планка её интегрированием по частотам. При этом постоянная Стефана Больцмана равна:
получается из формулы Планка её интегрированием по частотам. При этом постоянная Стефана Больцмана равна: 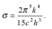 Закон смещения Вина получается при анализе формулы Планка на Экстремум
Закон смещения Вина получается при анализе формулы Планка на Экстремум 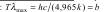 Таким образом формула Планка обобщает все законы теплового излучения и является полным решением основной задачи теории теплового излучения.
Таким образом формула Планка обобщает все законы теплового излучения и является полным решением основной задачи теории теплового излучения.
14. МАССА И ИМПУЛЬС ФОТОНА. Единство корпускулярных и волновых свойств света.
Используя соотношения 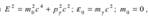 , получаем выражения для энергии, массы и импульса фотона:
, получаем выражения для энергии, массы и импульса фотона: 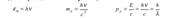 Эти соотношения связывают квантовые (корпускулярные) характеристики фотона — массу, импульс и энергию — с волновой характеристикой света — его частотой. Свет обладает одновременно волновыми свойствами, которые проявляются в закономерностях его распространения, интерференции, дифракции, поляризации, и корпускулярными, которые проявляются в процессах взаимодействия света с веществом (испускания, поглощения, рассеяния).
Эти соотношения связывают квантовые (корпускулярные) характеристики фотона — массу, импульс и энергию — с волновой характеристикой света — его частотой. Свет обладает одновременно волновыми свойствами, которые проявляются в закономерностях его распространения, интерференции, дифракции, поляризации, и корпускулярными, которые проявляются в процессах взаимодействия света с веществом (испускания, поглощения, рассеяния).
Давление света. Если фотоны обладают импульсом, то свет, падающий на тело, долженоказывать на него давление. Пусть поток монохроматического излучения частоты ν падает перпендикулярно поверхности. Если за 1с на 1м2 поверхности тела падает N фотонов, то при коэффициенте отражения ρ света от поверхности тела отразится ρN фотонов, а (1− ρ)N фотонов — поглотится. Каждый поглощенный фотон передает поверхности импульс pγ , а каждый отраженный фотон — 2pγ . Давление света на поверхность равно импульсу, который передают поверхности за 1с N фотонов: 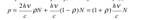 Энергетическая освещенность поверхности: Nhν = Ee (энергия всех фотонов, падающих на единицу поверхности в единицу времени). Объемная плотность энергии излучения,
Энергетическая освещенность поверхности: Nhν = Ee (энергия всех фотонов, падающих на единицу поверхности в единицу времени). Объемная плотность энергии излучения, 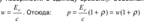 Волновая теория света на основании уравнений Максвелла приходит к такому же выражению. Давление света в волновой теории объясняется тем, что под действием электрического поля E(вектор) электромагнитной волны электроны в металле будут двигаться в направлении (обозначенном υ(вектор) на рисунке) противоположном E. Магнитное поле B(вектор) электромагнитной волны действует на движущиеся электроны с силой Лоренца в направлении (по правилу левой руки) перпендикулярном поверхности металла. Таким образом, электромагнитная волна оказывает на поверхность металла давление.
Волновая теория света на основании уравнений Максвелла приходит к такому же выражению. Давление света в волновой теории объясняется тем, что под действием электрического поля E(вектор) электромагнитной волны электроны в металле будут двигаться в направлении (обозначенном υ(вектор) на рисунке) противоположном E. Магнитное поле B(вектор) электромагнитной волны действует на движущиеся электроны с силой Лоренца в направлении (по правилу левой руки) перпендикулярном поверхности металла. Таким образом, электромагнитная волна оказывает на поверхность металла давление.
ЭФФЕКТ КОМПТОНА.
Корпускулярные свойства света отчетливо проявляются в эффекте Комптона — упругом рассеянии коротковолнового электромагнитного излучения (рентгеновского и γ -излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. Это увеличение 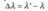 не зависит от длины волны λ падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния θ :
не зависит от длины волны λ падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния θ : 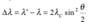 где λ′ — длина волны рассеянного излучения, λC — комптоновская длина волны. При рассеянии на электроне:
где λ′ — длина волны рассеянного излучения, λC — комптоновская длина волны. При рассеянии на электроне: 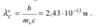
Фотон 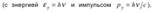 столкнувшись с электроном
столкнувшись с электроном 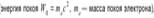 , передает ему часть своей энергии и импульса и изменяет направление движение (рассеивается). В процессе этого упругого столкновения выполняются законы сохранения
, передает ему часть своей энергии и импульса и изменяет направление движение (рассеивается). В процессе этого упругого столкновения выполняются законы сохранения 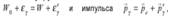 ,
, 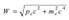 — релятивистская энергия электрона после столкновения, Таким образом
— релятивистская энергия электрона после столкновения, Таким образом 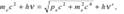 ,
, 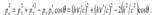 .
.  Эффект Комптона не может наблюдаться в видимой области спектра, поскольку энергия фотона видимого света сравнима с энергией связи электрона с атомом, при этом даже внешний электрон атома нельзя считать свободным. Эффект Комптона, излучение черного тела и фотоэффект служат доказательством квантовых (корпускулярных) редставлений о свете как о потоке фотонов.
Эффект Комптона не может наблюдаться в видимой области спектра, поскольку энергия фотона видимого света сравнима с энергией связи электрона с атомом, при этом даже внешний электрон атома нельзя считать свободным. Эффект Комптона, излучение черного тела и фотоэффект служат доказательством квантовых (корпускулярных) редставлений о свете как о потоке фотонов.
КВАНТОВАЯ ФИЗИКА
Идея опыта
Проводилось исследование отражения электронов от монокристалланикеля. Установка включала в себя монокристалл никеля, сошлифованный под углом, и установленный на держателе. На плоскость шлифанаправлялся перпендикулярно пучок монохроматических электронов.Скорость электронов определялась напряжением  на электронной пушке:
на электронной пушке: 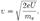
Под углом  к падающему пучку электронов устанавливался цилиндрФарадея, соединённый с чувствительным гальванометром. По показаниямгальванометра определялась интенсивность отражённого от кристаллаэлектронного пучка. Вся установка находилась в вакууме.
к падающему пучку электронов устанавливался цилиндрФарадея, соединённый с чувствительным гальванометром. По показаниямгальванометра определялась интенсивность отражённого от кристаллаэлектронного пучка. Вся установка находилась в вакууме.
В опытах измерялась интенсивность рассеянного кристаллом электронногопучка в зависимости от угла рассеяния 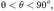 от азимутального угла
от азимутального угла 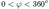 , от скорости
, от скорости  электронов в пучке.
электронов в пучке.
Опыты показали, что имеется ярко выраженная селективность(выборочность) рассеяния электронов. При различных значениях углов искоростей, в отражённых лучах наблюдаются максимумы и минимумыинтенсивности. Условие максимума: 
Здесь d — постоянная кристаллической решётки.
Таким образом наблюдалась дифракция электронов на кристаллическойрешётке монокристала. Опыт явился блестящим подтверждениемсуществования у микрочастиц волновых свойств.
Соотношение называется соотношением неопределенностей для величин A и B. Это соотношение ввёл в 1927 году Вернер Гейзенберг.
Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку меньше постоянной Планка h, называется соотношением неопределенностей Гейзенберга.
Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличии у нее волновых свойств. Т.к. в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.
Лазеры подразделяются:
-по типу активной среды (твердотельные, газовые, полупроводниковые и жидкостные)
-по методам накачки (оптические, тепловые, химические..)
-по режиму генерации (непрерывного или импульсного действия).
Свойства лазерного излучения:
Временная и пространственная когерентность.
Строгая монохроматичность
Большая плотность потока энергии
Очень малое угловое расхождение пучка.
ЯДЕРНАЯ ФИЗИКА
КАКОВО СОДЕРЖАНИЕ ПОНЯТИЙ ЗАРЯДНОГО И МАССОВОГО ЧИСЕЛ? КАКИЕ ЯДРА НАЗЫВАЮТСЯ: ИЗОТОПАМИ, ИЗОБАРАМИ, ИЗОТОНАМИ, ИЗОМЕРАМИ.
Общее число нуклонов в атомном ядре A называется массовым числом.
Заряд ядра равен величине Ze , где e — заряд протона, Z — зарядовое число ядра, равное числу протонов в ядре (совпадает с порядковым номером химического элемента в Периодической̆ системе элементов — атомным номером). Ядро химического элемента X с атомным номером Z и массовым числом A обозначается AZ X Поскольку атом нейтрален, то заряд ядра определяет число электронов в атоме, от которого зависит их распределение по состояниям в атоме, а следовательно, зависят химические свойства атома.
Изотопами называются ядра с одинаковым атомным номером Z (зарядом или числом протонов), но разными A (т.е. разным числом нейтронов N=A−Z). Например, изотопы водорода (Z =1): протий — 1H (Z =1,N=0),дейтерий̆— 21H (Z =1,N =1),тритий—31H (Z =1,N =2). Изобарами называются ядра с одинаковым массовым числом A, но разными Z . Например, 210 Tl , 210 Pb , 210 Bi . Изотонами называются ядра с одинаковым числом нейтронов N =A −Z . Н а п р и м е р , 13 6 C , 14 7 N , 1 58 O .
ПРАВИЛА СМЕЩЕНИЯ.
При радиоактивном распаде выполняется закон сохранения электрических зарядов:  и закон сохранения массовых чисел:
и закон сохранения массовых чисел: 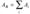 где Z Я e и AЯ — соответственно заряд и массовое число материнского ядра; Zie и Ai — соответственно заряды и массовые числа частиц, получившихся в результате радиоактивного распада. Следствием этих законов являются правила смещения, позволяющие установить, какое ядро возникает в результате распада данного материнского ядра в различных типах радиоактивного распада:
где Z Я e и AЯ — соответственно заряд и массовое число материнского ядра; Zie и Ai — соответственно заряды и массовые числа частиц, получившихся в результате радиоактивного распада. Следствием этих законов являются правила смещения, позволяющие установить, какое ядро возникает в результате распада данного материнского ядра в различных типах радиоактивного распада:
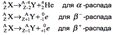
где AZ X — материнское ядро, Y — символ дочернего ядра, 42 He — ядро гелия (альфа-частица), -10 e — символическое обозначение электрона, а +10 e — позитрона — частицы с массой̆ покоя электрона, и спином 12 , несущей̆ положительный̆ электрический̆ заряд e .
Возникающие в результате радиоактивного распада ядра могут быть, в свою очередь, радиоактивными. Это приводит к возникновению цепочки, или ряда радиоактивных превращений, заканчивающихся стабильным элементом. Совокупность элементов, образующих такую цепочку, называется радиоактивным семейством. Естественно радиоактивные ядра образуют три радиоактивных семейства, называемых семейством урана ( 238 U ), семейством тория (90232 Th ) и семейством актиния ( 89235 Ac ), которые после цепочки альфа- и бетта- распадов заканчиваются на стабильных изотопах свинца 82206 Pb , 82208 Pb и 82207 Pb (имеющих особую устойчивость ядер, содержащих магическое число протонов — 82). Четвертое из известных семейств — семейство нептуния, начинается от трансуранового элемента 93237 Np, полученного искусственным путем, и заканчивается на висмуте 83209 Bi.
КОЛЕБАНИЯ И ВОЛНЫ
3) ЭЛЕКТРИЧЕСКИМ КОЛЕБАТЕЛЬНЫМ КОНТУРОМ называется электрическая цепь, состоящая из включенных последовательно катушки индуктивностью L , конденсатора емкостью C и резистора сопротивлением R . По закону Ома для участка цепи 
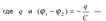 заряд конденсатора и разность потенциалов его обкладок в произвольный момент времени t; R − электрическое сопротивление колебательного контура; Θc − ЭДС самоиндукции в катушке. Сила тока
заряд конденсатора и разность потенциалов его обкладок в произвольный момент времени t; R − электрическое сопротивление колебательного контура; Θc − ЭДС самоиндукции в катушке. Сила тока 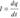 , поэтому дифференциальное уравнение колебаний заряда в колебательном контуре:
, поэтому дифференциальное уравнение колебаний заряда в колебательном контуре: 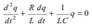
Стадии колебаний в идеализированном колебательном контуре.
Идеализированный колебательный контур — колебательный контур, у которого R = 0.
Пусть в начальный момент времени t = 0 конденсатор заряжен зарядом q . Тогда энергия электрического поля между обкладками конденсатора 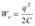
При замыкании конденсатора на катушку индуктивности, в контуре потечет возрастающий ток I . Энергия электрического поля начнет уменьшаться, а энергия магнитного поля катушки 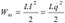 будет возрастать. Поскольку потерь в контуре нет (R = 0), то полная энергия W = We + Wm сохраняется.
будет возрастать. Поскольку потерь в контуре нет (R = 0), то полная энергия W = We + Wm сохраняется.
В момент времени t = 1/4T (T −период колебаний), когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля (а следовательно, и ток) достигает наибольшего значения.
Стадии колебаний в контуре можно сопоставить с аналогичными стадиями механических колебаний, например, математического маятника, который в момент времени t = 0 смещен из положения равновесия и имеет максимальную потенциальную энергию E =Umax . В момент времени t = 1/4T смещение маятника равно нулю, скорость — максимальна, и потенциальная энергия полностью переходит в кинетическую энергию маятника E = Kmax .
Начиная с момента времени t = 1/4T , ток в контуре будет убывать, следовательно, магнитное поле катушки начнет ослабевать. Изменение магнитного поля вызовет индукционный ток, который, по правилу Ленца, будет иметь то же направление, что и ток разрядки конденсатора. Конденсатор начинает перезаряжаться и к моменту времени t = 1/2T заряд на обкладках конденсатора достигнет максимума, ток в цепи прекратится, и энергия контура снова будет равна энергии электрического поля в конденсаторе.
Для маятника это будет соответствовать максимальному смещению в направлении, противоположном первоначальному, остановке маятника в крайнем положении (υ = 0) и обратному превращению кинетической энергии в потенциальную.
Далее, все процессы в колебательном контуре будут протекать в обратном направлении и система к моменту времени t = T придет в первоначальное состояние. Таким образом, в колебательном контуре происходят периодические изменения заряда q на обкладках конденсатора и силы тока I. Эти электрические колебания сопровождаются превращением энергий электрического и магнитного полей.
Из сравнения электрических колебаний с механическими колебаниями, следует, что:
- энергия электрического поля конденсатора аналогична потенциальной энергии маятника,
- энергия магнитного поля катушки аналогична кинетической энергии маятника,
- сила тока в контуре аналогична скорости движения маятника,
- индуктивность L выполняет функцию массы,
- сопротивление R играет роль силы трения, действующей на маятник.
ВОЛНОВОЙ ПРОЦЕСС.
Если возбудить колебания в какой-либо точке среды (твердой, жидкой или газообразной) то, вследствие взаимодействия между частицами среды, эти колебания будут передаваться от одной точки среды к другой со скоростью, зависящей от свойств среды. При рассмотрении колебаний не учитывается детальное строение среды; среда рассматривается как сплошная, непрерывно распределенная в пространстве и обладающая упругими свойствами. Среда называется линейной, если ее свойства не изменяются под действием возмущений, создаваемых колебаниями. Волновым процессом или волной — называется процесс распространения колебаний в сплошной среде. При распространении волны частицы колеблются около своих положений равновесия, а не перемещаются вслед за волной. Вместе с волной от частицы к частице передается только состояние колебательного движения и его энергия. Основным свойством всех волн является перенос энергии без переноса вещества.
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими.
Отличие графика волны от графика гармонического колебания:
1) график волны представляет зависимость смещения всех частиц среды от расстояния до
источника колебаний в данный момент времени ξ= ξ (x,t=const );
2) график гармонического колебания это зависимость смещения данной частицы от
времени ξ =ξ(x = const,t).
Бегущими волнами называются волны, которые переносят в пространстве энергию.
Перенос энергии количественно характеризуется вектором плотности потока энергии (вектор Умова). Направление этого вектора совпадает с направлением распространения энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно волне. Важными примерами бегущих волн являются плоская и сферическая волны. Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу.
Волна называется сферической, если ее волновые поверхности имеют вид концентрических сфер. Центры этих сфер называются центром волны.
11) Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных: 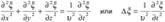 где υ — фазовая скорость,
где υ — фазовая скорость, 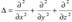 — оператор Лапласа Решением волнового уравнения является уравнение любой волны (в том числе и плоская и сферическая волны). Интерференцией волн называется явление наложения волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других в зависимости от соотношения между фазами этих волн. Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками, колеблющимися с одинаковыми амплитудой A0, частотой ω и постоянной разностью фаз:
— оператор Лапласа Решением волнового уравнения является уравнение любой волны (в том числе и плоская и сферическая волны). Интерференцией волн называется явление наложения волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других в зависимости от соотношения между фазами этих волн. Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками, колеблющимися с одинаковыми амплитудой A0, частотой ω и постоянной разностью фаз:
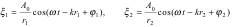 где r1 и r2 — расстояния от источников до рассматриваемой точки, k — волновое число, ϕ1 и ϕ2 — начальные фазы волн.
где r1 и r2 — расстояния от источников до рассматриваемой точки, k — волновое число, ϕ1 и ϕ2 — начальные фазы волн.
Поскольку для когерентных источников ϕ1 − ϕ2 = const , то результат интерференции двух волн зависит от величины (r1 − r2) , называемой разностью хода. Интерференционный максимум (A = A0/r1 + A0/r2) наблюдается в точках, где k(r1 − r2) − (ϕ1 −ϕ2) = ±2m (m = 0,1, 2,K) π Интерференционный минимум (A = |A0/r1 - A0/r2|) наблюдается в точках, где k(r1 − r2) − (ϕ1 −ϕ2) = ±(2m +1)π
Дата: 2019-07-24, просмотров: 462.